LiNi0.5Mn1.5O4电极的变固相扩散系数模拟
2017-07-18吕桃林晏莉琴解晶莹
吕桃林,罗 英,晏莉琴,解晶莹
( 1.哈尔滨工业大学化工学院,黑龙江 哈尔滨 150001; 2.上海动力储能电池系统工程技术有限公司,上海 200245; 3.上海空间电源研究所,上海 200245 )
·理论研究·
LiNi0.5Mn1.5O4电极的变固相扩散系数模拟
吕桃林1,2,3,罗 英1,2,3,晏莉琴2,3,解晶莹1,2,3
( 1.哈尔滨工业大学化工学院,黑龙江 哈尔滨 150001; 2.上海动力储能电池系统工程技术有限公司,上海 200245; 3.上海空间电源研究所,上海 200245 )
通过实验和参数辨识,确定了针对LiNi0.5Mn1.5O4体系电池所需要的模型参数,建立了适用于该体系的变固相扩散系数模型。该模型能很好地对LiNi0.5Mn1.5O4的放电过程进行模拟。通过对电池内部的过电位进行分析,对电池性能的限制因素进行了说明。
LiNi0.5Mn1.5O4; 变固相扩散系数(VSSD)模型; 过电位; 锂离子电池
LiNi0.5Mn1.5O4由于具有高比容量及较高的电压平台(4.7 V),引起了人们的极大兴趣[1]。通过合适的数值模型,可深入理解电池内部物理化学过程及限制因素,为电池的优化设计提供参考。目前应用较广泛的模型是J.S.Dunning等[2]建立的P2D模型,以多孔电极理论和浓溶液理论为基础,对锂离子电池内部的物理化学过程进行描述[3]。该模型将固相传输过程视为单相扩散过程,未对材料在工作过程中可能发生的相变过程进行分析。LiNi0.5Mn1.5O4在充放电过程中有两个电位平台,分别对应Ni的两次价态变化。研究表明:镍锰酸锂材料在Li+嵌脱过程中经历了相转变过程。需要对现有模型进行修正,以建立适用于该体系的数值模型。涉及相变的传统材料有磷酸铁锂、钴酸锂等,针对这些材料的相变过程,研究者提出了收缩核模型、相场模型和固溶体模型[4]和变固相扩散系数(VSSD)模型等[5]。VSSD模型避免对相变过程的具体模拟,同时包含该过程的主要特征。
本文作者建立了适用于LiNi0.5Mn1.5O4体系的VSSD模型,同时确定了模型中所需要的参数。对材料工作中的内部过程进行分析,同时,对LiNi0.5Mn1.5O4的过电位进行分解,分析电池放电过程中的限制因素,为材料的优化设计提供参考。
1 模型的建立
研究对象是以金属锂作为对电极的二电极体系,在P2D模型中引入VSSD模型。VSSD模型用于模拟固相内部的传输过程,P2D模型用于模拟电极过程[5-6]。
VSSD模型基于二元溶液热力学对固相内部的传输过程进行描述,将活性物质视为空位与锂位构成的非理想二元溶液。用吉布斯自由能分析它们之间的相互作用力,同时忽略充放电过程中的体积变化,将颗粒内部的物质传递表示为[5-6]:
(1)
式(1)中Ds′是二元扩散系数,为常数;cs是固相Li+浓度;α为固相热力学因子,由电极的平衡电位得到,表示为[5-6]:
(2)
式(2)中:γ是固相内Li+活度系数,Us为平衡电位,y为嵌锂量。如果用稀溶液理论表示,根据Fick第二扩散定律求解,物质传递表达式为[5-6]:
(3)
式(3)中:Ds为菲克扩散系数(即αDs′)。
利用Butler-Volmer方程描述电化学反应过程,用反应物质流表示颗粒表面Li+的脱嵌过程,则粒子表面的反应离子流密度与表面上的过电势的关系为:
(4)
式(4)中:JJ为活性颗粒表面离子流通量;αa、αc为反应传递系数;j0为交换电流密度;η为表面过电位。交换电流密度表示为:
(5)
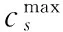
η=Φs-Φe-Us
(6)
式(6)中:Φs为固相表面电位,Φe为液相电位。
2 实验
2.1 电池的制作
将LiNi0.5Mn1.5O4(上海产,电池级)与乙炔黑(上海产,电池级)、聚偏氟乙烯(广州产,电池级)按质量比8∶1∶1混匀,加入适量溶剂N-甲基吡咯烷酮(广州产,AR)搅拌均匀,涂覆在16 μm厚铝箔(上海产,电池级)上,在80~120 ℃下干燥24 h,再冲成直径为12 mm的极片。以金属锂片(上海产,电池级)为负极,1 mol/L LiPF6/EC+EMC(体积比3∶1,深圳产,电池级)为电解液,在高纯氩气保护的手套箱中组装CR2032型扣式电池。
2.2 性能测试
组装好的电池在CT2001A 5 V/2 mA充放电测试仪(武汉产)上,以0.10C在3.5~4.9 V循环20次,进行活化。以极小倍率(0.01C)对电池进行充放电,通过对充放电数据进行归一化处理,取平均值作为LiNi0.5Mn1.5O4的平衡电位;在不同荷电状态(SOC)下(以0.6 mA放电2 min,不同状态之间的间隔为0.02 mAh)进行不同倍率的恒流间歇滴定,通过充放电前后的平衡电位差值,对固相扩散系数进行计算;在不同SOC进行小倍率脉冲,通过放电时刻的电位阶跃,对电化学反应系数进行计算;材料的初始嵌锂量通过测量平衡电位得到。此外,由于部分参数会在电池工作过程中发生变化或不方便测量,通过不同倍率放电测试,利用参数辨识的方法进行整体调整,以确定模型中所需要的参数。所选倍率分别为:0.05C(0.03 mA)、0.10C、0.20C、0.50C和1.00C。所有测试均在恒温(25 ℃)下进行。
3 结果与讨论
3.1 参数提取
为方便研究,在对镍锰酸锂的平衡电位进行测试后,对结果进行拟合,如图1所示。
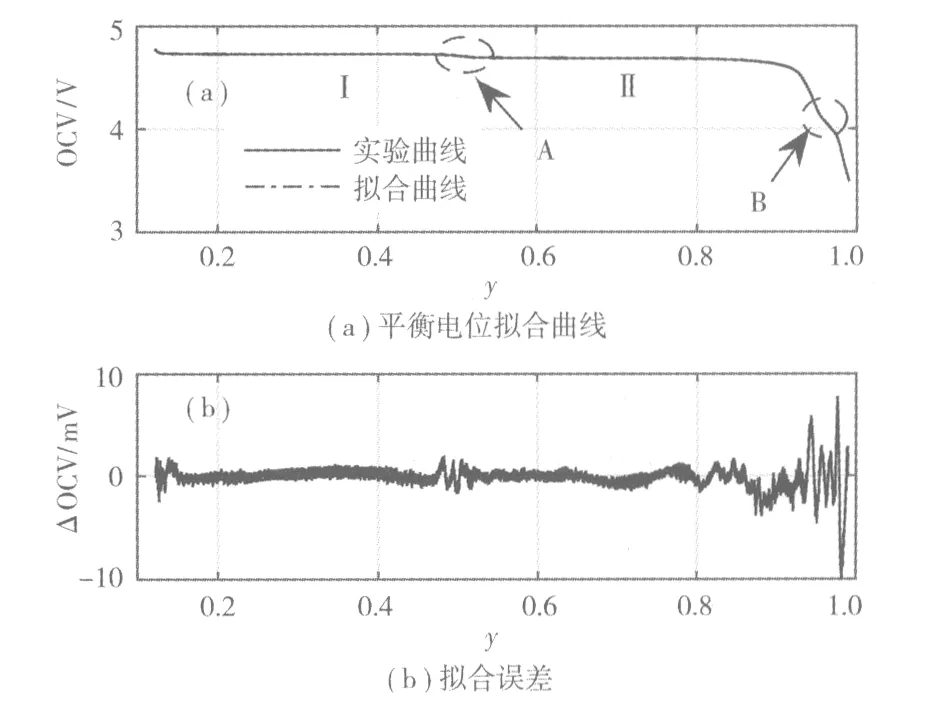
图1 LiNi0.5Mn1.5O4平衡电位曲线Fig.1 Equilibrium potential curves of LiNi0.5Mn1.5O4
从图1可知,实验过程对平衡电位进行了较好的拟合。LiNi0.5Mn1.5O4在放电过程中存在两个电压平台,分别为4.73 V与4.69 V,标记为Ⅰ、Ⅱ;存在两次较明显的电压转折,标记为A、B,可能对应着LiNi0.5Mn1.5O4的结构转变。
为了对VSSD模型进行验证,通过恒流间歇滴定,测量固相扩散系数随嵌锂量的变化情况。恒流间歇滴定示意图见图2。
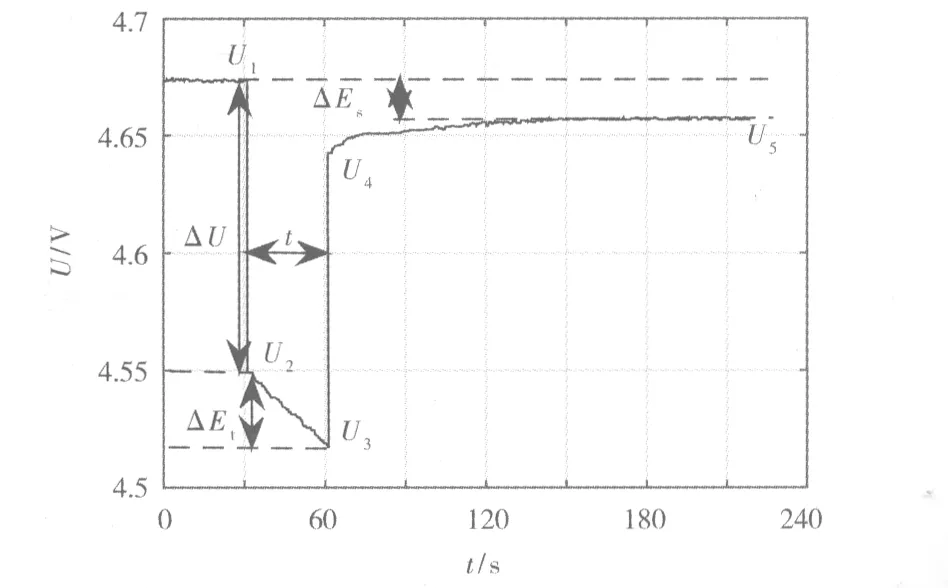
图2 恒流间歇滴定示意图Fig.2 Galvanostatic intermittent titration technique
从图2可知,恒流间歇滴定过程中,有5个电位变化,其中,U1为起始平衡电位,U2为滴定开始时的电位,U3为滴定过程中的电位变化,U4为滴定结束时的电位,U5为滴定结束后的平衡电位。通过测试电极电位随时间的变化,通过以下公式计算材料的固相扩散系数[7]:
(7)
式(7)中:t为放电时间,mB为活性物质质量,VM为活性物质的摩尔体积,MB为活性物质相对分子质量,S为极片的面积,△Et为放电过程中的电压阶跃(即U2-U3),△Es为稳态电位变化(即U1-U5)。
通过在不同SOC下对电池进行恒流间歇滴定(GITT),可以得出LiNi0.5Mn1.5O4在放电过程中的扩散系数的变化情况,测试过程如图3所示。
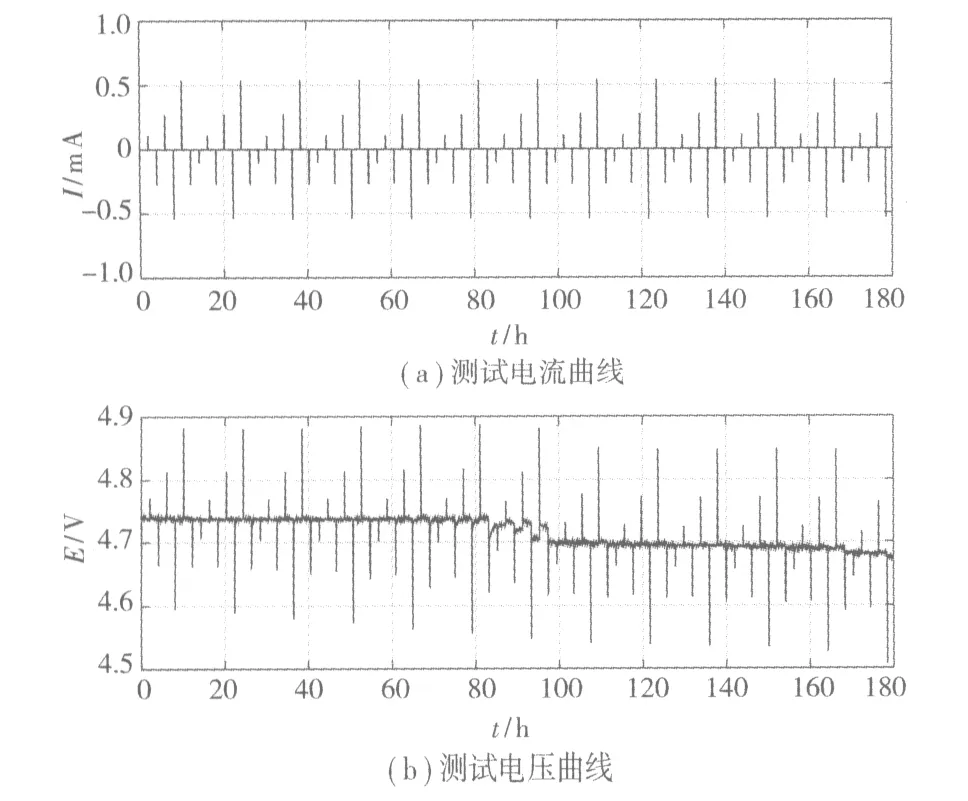
图3 恒流间歇滴定(GITT)测试过程Fig.3 Galvanostatic intermittent titration(GITT) test procedure
可根据式(2),通过平衡电位曲线计算得到的材料的热力学因子,并结合菲克扩散系数,得出LiNi0.5Mn1.5O4在放电过程中的扩散系数变化情况。通过GITT以及热力学因子计算所得结果见图4。
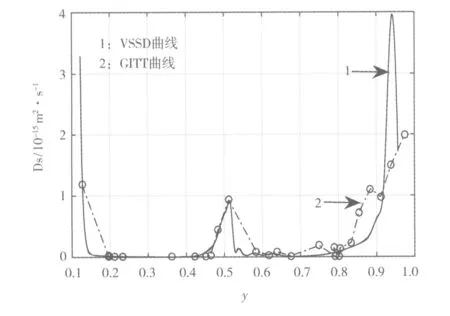
图4 固相扩散系数随嵌锂量的变化情况Fig.4 The change of solid diffusion coefficient with lithium intercalation
通过对比恒流间歇滴定的测试结果与根据式(2)计算的结果可知,在整个放电区间内,两种方式所得的固相扩散系数基本吻合,因此认为VSSD模型中假设的变固相扩散系数反映了LiNi0.5Mn1.5O4材料的本身性质,可用于进行模拟。在放电末期出现较大偏差,可能是放电末期电池很难达到平衡所致。
从图4可知,LiNi0.5Mn1.5O4的固相扩散系数随嵌锂量呈现马鞍状变化。通过与平衡电位的变化情况对比可知,在平衡电位变化较快的阶段,扩散系数较大;在平衡电位平台区域,扩散系数明显减小;在电位平台阶跃区域,扩散系数有所抬升。这可能与材料在不同嵌锂状态下,Li+之间的相互作用力有关,也可能与材料在充放电过程中的晶格变化有关。
此外,可通过对P2D模型的简化,方便地对材料充放电过程中的电化学反应系数进行研究。首先假设在小电流放电过程中电化学反应分布符合单粒径模型,即满足式(8):
(8)
定义参考电位为Φe|x=0=0,则可得金属锂的电极电位为:
(9)
式(9)中Φs,Li为金属锂的电极电位,J为放电电流密度,j0,Li为金属锂的交换电流密度。
其次,在放电电流较小的情况下对Butler-Volmer方程(4)进行线性简化,即:
(10)
然后,根据过电位公式(6),可将阶跃电位表示为:
(11)
由于没有液相浓度极化且反应均匀分布,因此可对液相电位分布进行简化:
(12)
(13)
再结合式(10)—式(12),将LiNi0.5Mn1.5O4的交换电流密度表示为:
(14)
最后,结合交换电流密度公式(5),可将LiNi0.5Mn1.5O4的电化学反应系数表示为:

(15)
可通过小电流脉冲测试,对LiNi0.5Mn1.5O4的电化学反应系数进行估算。对电池进行小倍率脉冲放电时,电位变化曲线与图3相同,其中△U为阶跃电位。脉冲测试中采用较小电流,结果如图5所示。
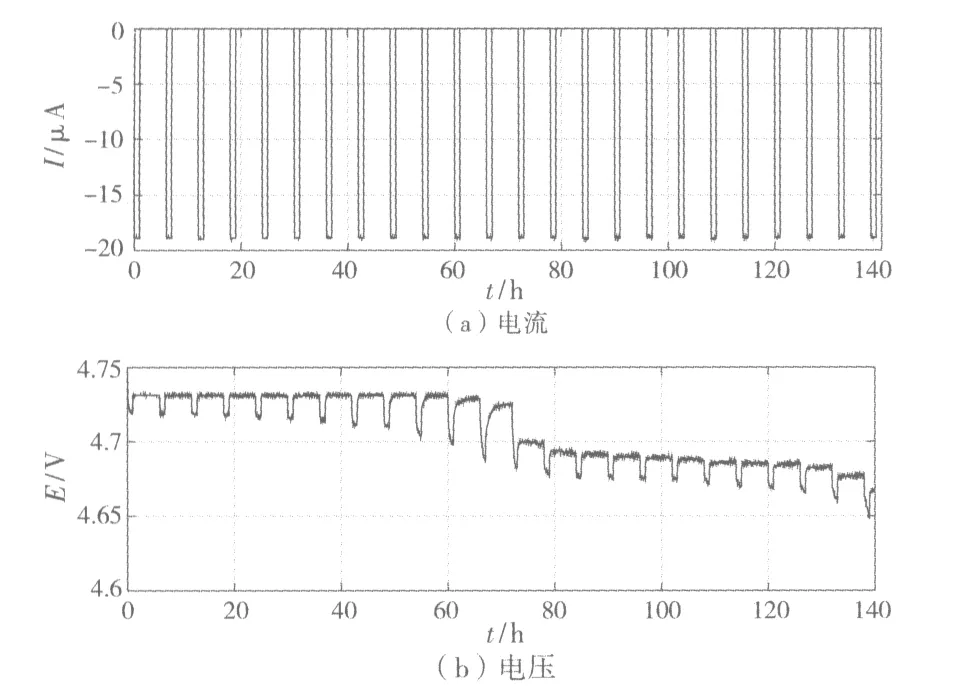
图5 脉冲测试过程Fig.5 Impulse test procedure
根据式(15)对LiNi0.5Mn1.5O4在反应过程中的电化学反应常数进行计算,所得结果如图6所示:
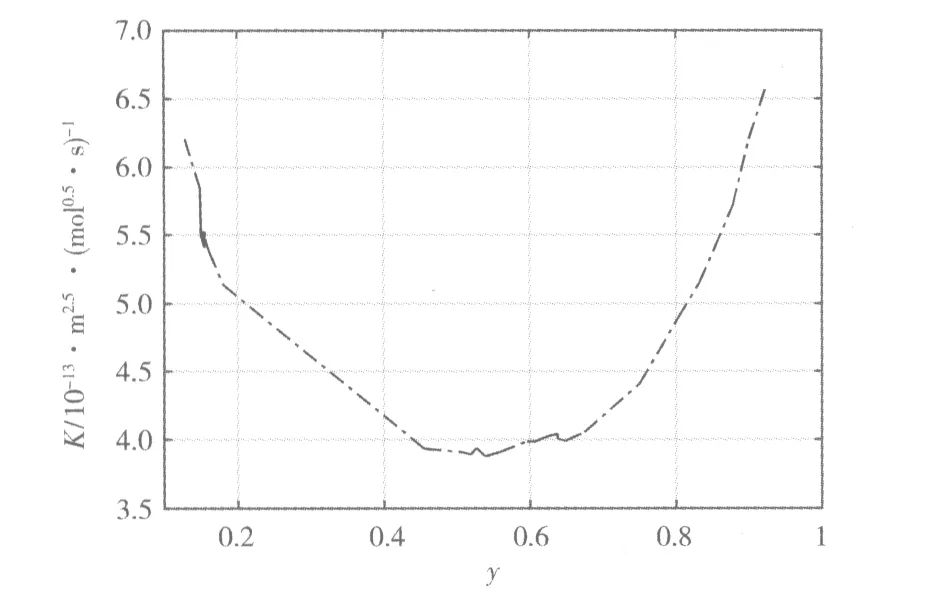
图6 不同嵌锂量下LiNi0.5Mn1.5O4的电化学反应常数Fig.6 Rate constant of the LiNi0.5Mn1.5O4 electrode as a function of y
从图6可知,LiNi0.5Mn1.5O4的电化学反应常数在放电过程中基本维持在同一数量级,因此可根据该实验结果,对仿真结果进行调整优化。针对电池模型计算所需要的参数见表1。
在电池仿真过程中,以实验电流值作为输入工况,同时根据电池工作前的搁置电位作为平衡电位,计算电极起始嵌锂量,参数ys,0(0.05C)、ys,0(0.10C)、ys,0(0.20C)、ys,0
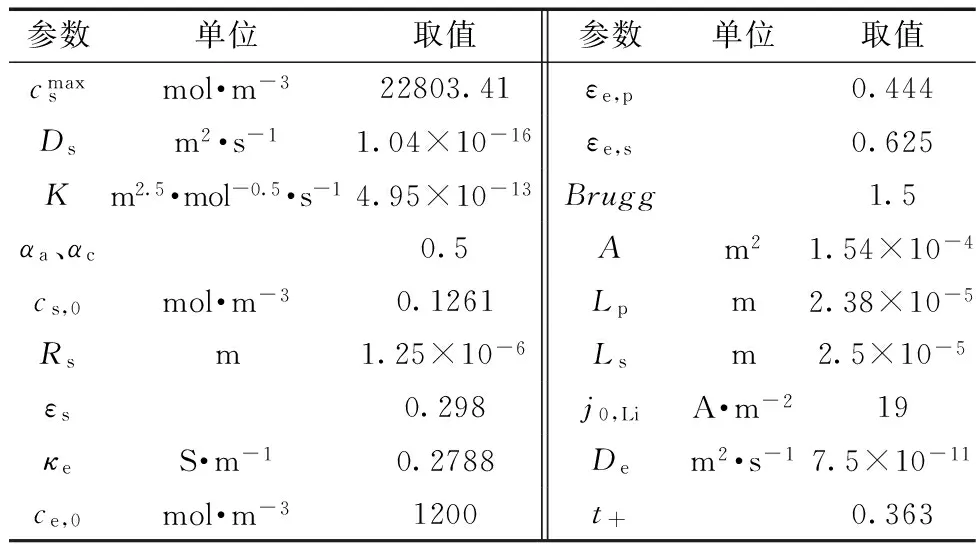
表1 模型参数Table 1 Model parameters
(0.50C)和ys,0(1.00C)的取值分别为0.1261、0.1265、0.1285、0.1314和0.1291。
3.2 实验仿真
根据所建立的VSSD模型,对电池不同倍率的放电曲线进行仿真,并与实验所得数据进行对比,如图7所示。
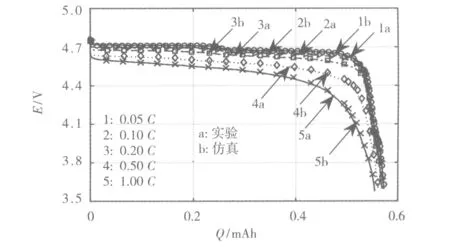
图7 实验数据与仿真数据对比Fig.7 Comparison of experiment data and simulation data
从图7可知,镍锰酸锂在放电过程中有两个明显的放电平台,且在放电末期有一个不明显的电压拐点,与该材料的平衡电位对应。随着放电倍率的增大,受极化作用的影响,平台拐点逐渐消失。VSSD模型的结果与实验数据吻合,说明所建立的VSSD模型可真实地反映镍锰酸锂的工作过程。
3.3 内部分析
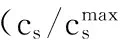
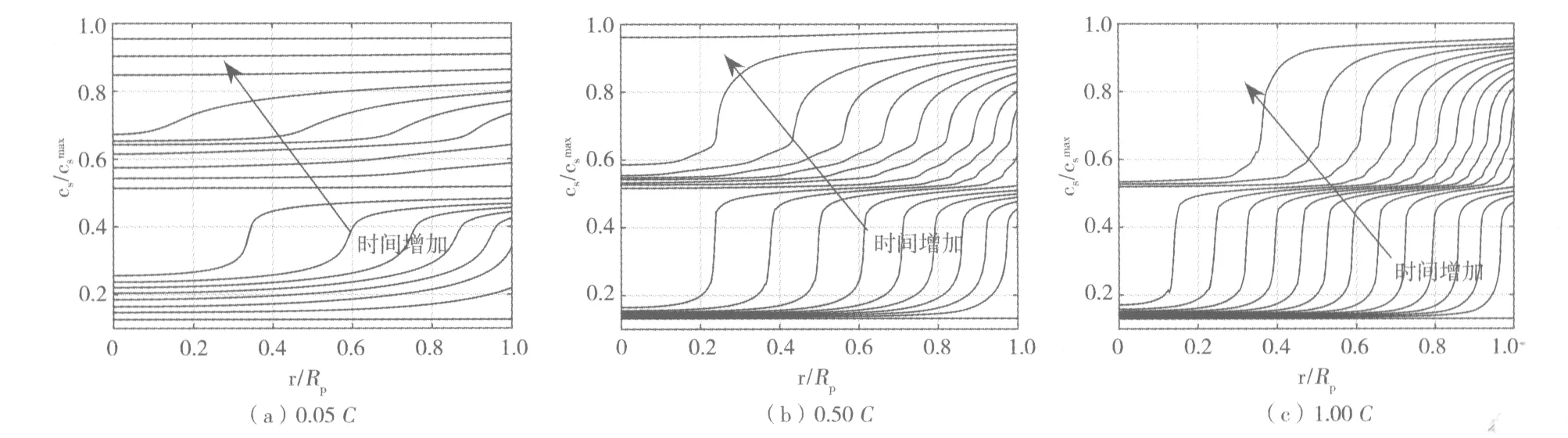
图8 不同倍率放电下固相浓度分布仿真结果Fig.8 Concentration profiles of intercalated lithium within particle simulated by the VSSD model over the course of discharge
从图8可知,在放电过程中,材料经历了两次界面浓度阶跃过程。在放电初始阶段,当材料表面嵌锂量达到0.15左右时,由于扩散系数急剧下降,使得Li+在颗粒表面累积,界面浓度迅速升高,形成与固相内部的浓差界面。在之后的放电过程中,该界面逐渐向内迁移。当表面嵌锂量达到0.5左右时,由于扩散系数增加,使得浓差界面消除。随着放电继续,当表面嵌锂量达到0.6时,由于固相扩散系数又一次减小,使得浓差界面再次形成,但第二平台上的扩散系数较第一平台上扩散系数大,使得浓差界面的迁移并不明显。当放电接近拐点,即表面嵌锂量达到0.9左右时,由于扩散系数急剧升高,使得浓差界面消失,固相内部浓度梯度减小。随着放电倍率的增大,材料表面嵌锂量累积速度增加,达到扩散系数降低阶段的时间逐渐缩短,因此形成的浓差界面的时间逐渐缩短,且浓差界面逐渐明显。同时,随着倍率的增加,两次浓差界面之间的过渡区间逐渐减小,这主要是由于随着倍率的增加,浓度变化速度变快引起的。
3.4 电位分解
利用数值模型,可进一步对电池工作过程中的电位发展进行分析。在放电过程中,电池的电位是由理想平衡电位以及各种极化电位组合而成的:
(16)
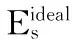
通过VSSD模型,对1.00C放电过程中的电位分解与各极化过电位分析如图9和图10所示。
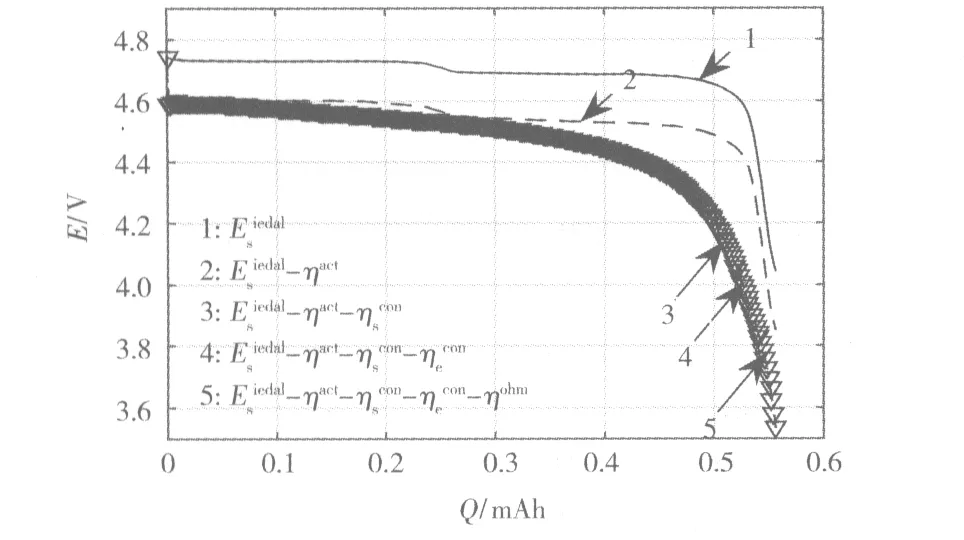
图9 电池放电电压分解Fig.9 Battery discharge potential decomposition
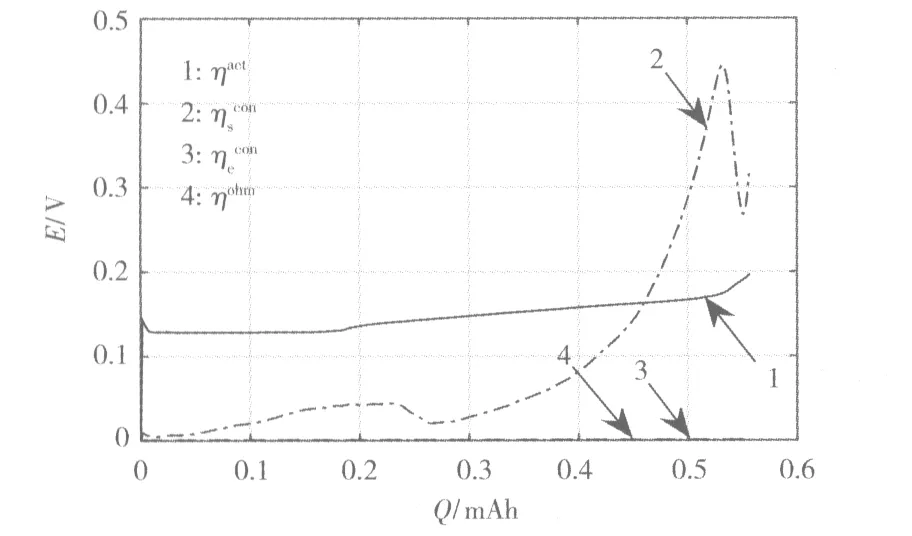
图10 电池放电过电位分析Fig.10 Battery discharge over potential analysis
从图9和图10可知,在各极化过电位中,反应极化过电位与固相浓差极化过电位为主导。反应极化过电位主要受材料反应极化系数的影响;固相浓差极化过电位在放电末期急剧增大,主要受与固相扩散有关的材料粒径及扩散系数的影响。
基于电池电位的分解,对影响电池主要性能的反应极化系数、固相扩散系数及粒径的敏感度进行分析,参数取值见表2。

表2 模型输入参数范围Table 2 The range of model parameters
1.00C放电下各参数的敏感度如图11所示。
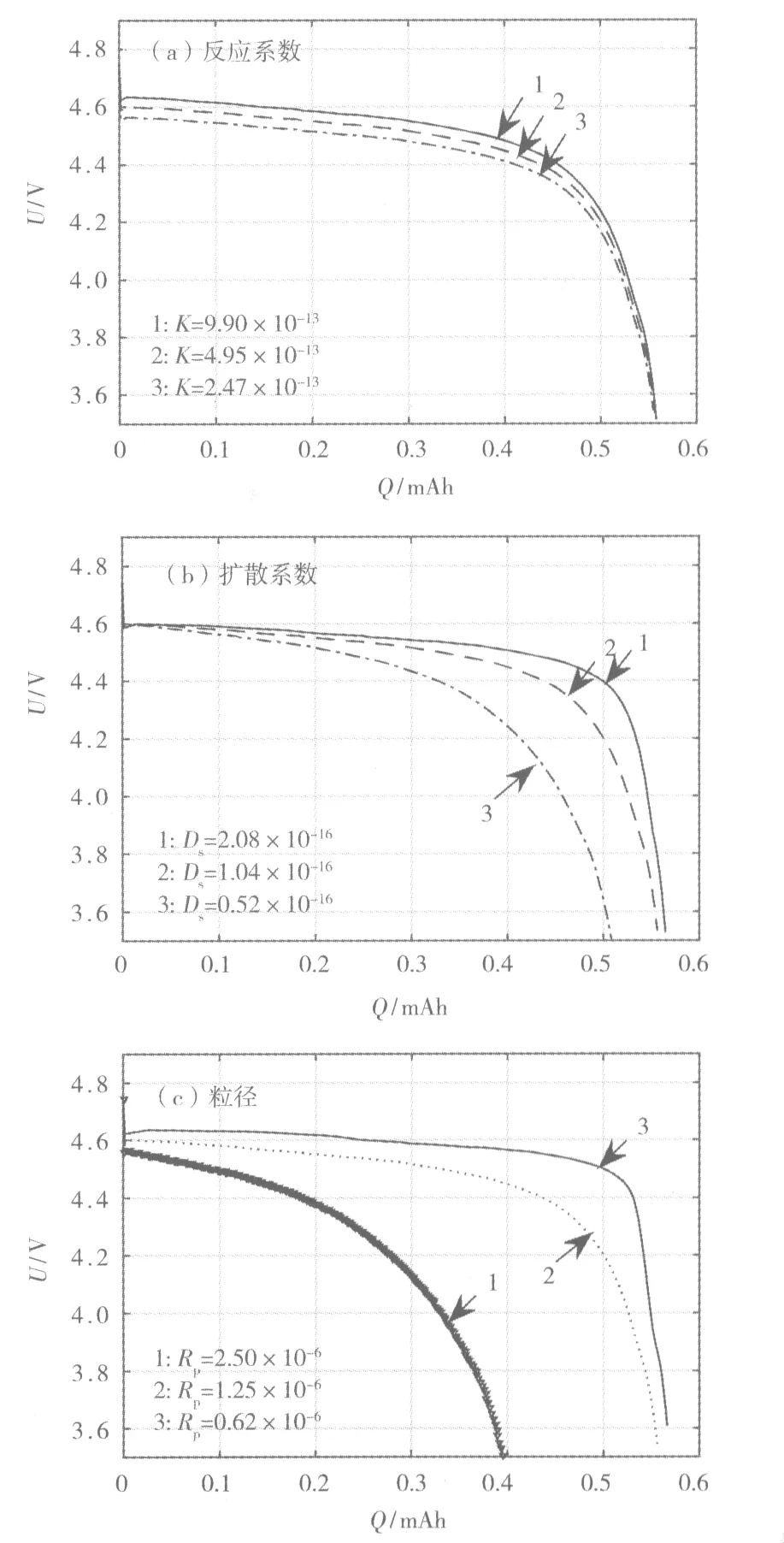
图11 1.00 C放电下不同参数的敏感度分析Fig.11 Sensitivity of different parameters at 1.00 C discharge
从图11可知,反应系数通过影响反应极化过电位主要对电池放电过程中的放电平台产生影响;固相扩散系数与材料粒径通过影响固相浓差极化过电位在放电末期急剧增大,主要对电池的放电容量产生影响。目前针对LiNi0.5Mn1.5O4的改性研究主要集中在控制形貌、掺杂离子以及包覆等。可通过仿真对材料的合成改性提供一定的帮助,如通过控制材料形貌与粒径,可改善材料的容量性能;通过掺杂提高材料的反应能力,可改善材料的功率特性,提高材料的功率密度。
4 结论
通过对LiNi0.5Mn1.5O4材料参数的测定辨识,建立了适用于该材料体系的变固相扩散系数模型,对LiNi0.5Mn1.5O4的工作过程进行了仿真。对放电过程中颗粒浓度的分布情况进行仿真,由于扩散系数的改变,在放电过程中颗粒内部发生了两次浓度阶跃。通过模拟不同参数对电池性能的影响,对材料的限制因素进行分析,为材料的改性方向提供了一定的指导。
[1] SANTHANAM R,RAMBABU B.Research progress in high voltage spinel LiNi0.5Mn1.5O4material [J].J Power Sources,2010,195(17):5 442-5 451.
[2] DUNNING J S,BENNION D N,NEWMAN J.Analysis of porous electrodes with sparingly soluble reactants [J].J Electrochem Soc,1971,118(8):1 251-1 256.
[3] 罗玲,宋文吉,林仕立,etal.锂离子电池热模型的研究现状 [J].电池,2015,45(5):280-283
[4] SRINIVASAN V,NEWANM J.Discharge model for the lithium iron-phosphate electrode [J].J Electrochem Soc,2004,151(10):1 517-1 529.
[5] FARKHONDEH M,DELACOURT C.Mathematical modeling of commercial LiFePO4electrodes based on variable solid-state diffusivity [J].J Electrochem Soc,2012,159(2):177-192.
[6] FARKHONDEH M,SAFARI M,PRITZKER M,etal.Full-range simulation of a commercial LiFePO4electrode accounting for bulk and surface effects:a comparative analysis [J].J Electrochem Soc,2014,161(3):201-212.
[7] LIU P,WU H.Diffusion of lithium in carbon [J].Solid State Ionics,1996,92(1-2):91-97.
[8] RAHIMIAN S K,RAYMAN S.WHITE R E.Extension of physics-based single particle model for higher charge-discharge rates [J].J Power Sources,2013,224(4):180-194.
收稿日期:2017-01-04
Modeling of LiNi0.5Mn1.5O4electrodes based on variable solid-state diffusivity
LV Tao-lin1,2,3,LUO Ying1,2,3,YAN Li-qin2,3,XIE Jing-ying1,2,3
(1.SchoolofChemicalEngineering&Technology,HarbinInstituteofTechnology,Harbin,Heilongjiang150001,China;2.ShanghaiPowerEnergyStorageBatterySystemEngineeringTechnologyCo.,Ltd.,Shanghai200245,China;3.ShanghaiInstituteofSpacePowerSources,Shanghai200245,China)
By adopting experiment and parameter recognition method,it was confirmed that a larger number of parameters which needed for the model of new system could setup a suitable model that involved variable solid-state diffusivity (VSSD).The model was used to simulate performance of LiNi0.5Mn1.5O4electrodes.The model was validated that it could be used to better simulate the discharging processes of LiNi0.5Mn1.5O4,by analyzing the over potential of battery and explaining its limiting factors.
LiNi0.5Mn1.5O4; variable solid-state diffusivity(VSSD) model; over potential; Li-ion battery
2016-11-08
吕桃林(1986-),男,河南人,哈尔滨工业大学化工学院博士生,研究方向:锂离子电池仿真;
10.19535/j.1001-1579.2017.02.006
TM912.9
A
1001-1579(2017)02-0084-06
罗 英(1987-),女,重庆人,哈尔滨工业大学化工学院博士生,研究方向:锂离子电池电解液;
晏莉琴(1975-),女,湖北人,上海动力储能电池系统工程技术有限公司高级工程师,研究方向:锂离子电池系统;
解晶莹(1971-),女,黑龙江人,上海空间电源研究所总研究师,研究员,研究方向:锂离子电池,本文联系人。
