基于膜计算模型的数独游戏基本解法*

江 赟

(重庆工商大学 重庆市检测控制集成系统工程实验室，重庆 400067)

基于膜计算模型的数独游戏基本解法*

江 赟

(重庆工商大学 重庆市检测控制集成系统工程实验室，重庆 400067)

为了更好地求解数独问题，提出了一种新的求解方法，利用一个具有抑制催化和膜溶解规则以及进化规则的优先级的膜系统来进行求解；结果表明，对于一个数独问题，只要其所有部分解都至少包含一个具有唯一解的单元格，方法都是有效的；如果数独问题可以利用此策略求解，则膜系统在计算的最后一步将问题的解编码并返回物质YES，否则，膜系统可以检测出数独问题不符合上述特征，返回物质NO，计算停止；方法求解策略与人类求解数独问题的思考过程非常类似，并且给出的是数独问题的统一解，即与数独问题的维度和提示数无关。

膜计算；数独游戏；细胞膜系统

数独游戏(Sudoku)是一种非常受欢迎的数学智力拼图游戏，它既不需要丰富的百科知识，也不需要掌握大量的词汇，是老少皆宜的游戏。传统的9×9格子数独游戏(九宫数独)的形式如图1所示，为了方便描述，用数字1～9来标识行(row)和列(column)，这样每个小单元格(cell)就有了坐标。这81个单元格又组成9个小九宫格(box)，分别标记为1～9。数独游戏的规则很简单，在81个单元格中填入数字1～9，要求填入的数字在每行和每列都不能有重复，同时在每个小九宫格中也不能有重复。游戏开始时会将一些位置上的数字固定下来，这称为提示数(或起始数)，根据提示数的位置和数量可以将数独游戏分为不同的难度等级。

图1 一个简单的数独例子Fig.1 A simple example of Sudoku

数独游戏不仅具有娱乐性，而且从数学的角度看具有重要的性质。标准九宫数独一共有6 670 903 752 021 072 936 960=9!×722×27×27 704 267 971种合法的数独终盘，其中最后一个因子是质数[1]。其次，求解n2×n2个单元格的数独问题已被证明是一个NP完全问题[2]。

用计算机求解数独问题最原始的方法是暴力破解法，即用穷举的办法遍历整个解空间，这种方法的遍历和回溯都是在最大深度上进行的，需要大量的时间和内存。目前有多种方法求解数独问题。文献[3]利用约束规划的方法，通过设置一个目标函数与约束函数，采用分支定界法求解。文献[4]将数独问题转化为组合优化问题，然后利用编码、初始化、交叉、变异及局部搜索具有特点的遗传算法来进行求解。文献[5]将数独问题转化为一个1范数的优化问题，然后通过引入松弛变量，转化为一个线性规划问题，再利用算法进行快速求解。文献[6]采用分布式势博弈方法进行求解，将数独问题转化为势博弈模型，然后利用学习动力进行逐步优化以达到势博弈的最优状态——纳什均衡点。

提出一种新的求解思路，使用膜计算求解数独问题。对于一个n维的数独，只要其所有部分解都至少包含一个具有唯一解的单元格，就可以构造一族膜系统来进行求解。这一族膜系统中每一个膜系统∏(n)是一个具有输入的膜系统，数独问题编码为一个多重集作为输入。求解的基本思想是利用膜计算中的抑制催化、膜溶解及规则间的优先级等操作来寻找只有一个候选数的单元格。如果数独问题可以利用此策略求解，则膜系统在计算的最后一步将问题的解编码并返回物质YES，否则，膜系统可以检测出数独问题不符合上述特征，返回物质NO，计算停止。这种求解策略非常类似人类求解数独问题的思考过程[7]。

1 模 型

膜计算是自然计算的一个分支，由欧洲科学院院士、罗马尼亚科学院院士Gheorghe Paun于1998年在芬兰图尔库计算机科学中心提出[8]。膜计算是当前计算机科学、数学、生物学等多学科交叉的研究热点，旨在从活细胞的结构和功能中以及从组织和器官等细胞群的协作中抽象出计算模型，即膜计算模型(或称为膜系统)。膜计算模型具有良好的分布式结构和并行处理信息能力。截至目前，主要有3种类型的膜计算模型：细胞膜系统[8]、组织膜系统[9]和神经膜系统[10]。关于膜计算的详细内容，可以参考膜计算网站及相关专著[11-12]。所采用的是细胞膜系统，计算模型是模仿细胞的结构和功能，其基本组成要素包括膜结构、对象和规则。

所采用的膜系统使用了以下类型的规则：

(2) 膜溶解规则：[u]e→o，多重集u导致膜e溶解，并且生成物质o。

(3) 物质输出规则：[a]e→[]ea，物质a被送出标记为e的膜。

此外，在使用规则时系统还用到了规则间的优先级。

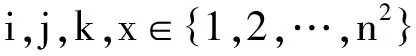
具体来说，求解数独问题的一族膜系统的结构如下：

膜系统的字母表为

膜的标记集合为H={0,1}

膜结构为μ=[[]1]0

系统处于初始组态时膜1和膜0中对象多重集分别为

当膜系统求解一个具体的数独问题时，膜1中还应包含编码为zijm的问题的输入。

i0=1，即输入膜为膜1。

系统的规则如下所示:

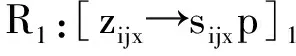
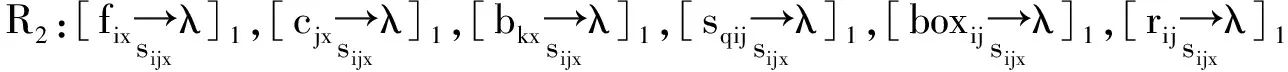
R3:[,[其中i,j,x∈{1，2,…，n2}

R4:[d,其中i,j∈{1，2,…，n2}

R6:[，其中i,j,x∈{1，2,…，n2}

R7:[，其中i,j,x,q∈{1，2,…，n2}

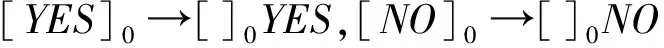
利用上述膜系统求解数独问题的总体思想是将求解过程分为两个阶段：检查阶段和重启阶段。在检查阶段，膜系统查找只有一个候选数的单元格。一旦找到了这样的单元格，则候选数填入其中。在检查阶段后，系统进入重启阶段，所有的辅助对象在此阶段重新计算，然后系统又开始进入检查阶段。当所有的单元格都填入了数字，求解完毕，或者在某个检查阶段没有找到只有一个候选解的单元格时，这个检查-重启循环结束。

2 求 解

用一个如图2所示的九宫数独的求解过程来解释上述膜系统。

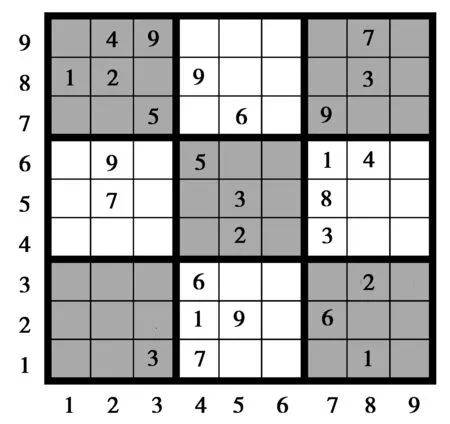
图2 一个3维的数独问题Fig.2 A Sudoku problem of order 3

如图2所示，数独问题有27个提示数，相应地，系统的输入即数独问题编码为z133z147z181z241z259z276z346z382z452z473z527z553z578z629z645z671z684z735z756z779z811z822z849z883z924z939z987。

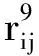
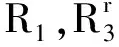
由于系统中不再有物质zijx，因此集合R1中的规则不再适用。此时，系统处于组态C1，集合R2中的规则适用，表1的对象从膜1中移除，系统进化到组态C2。

表1 系统处于组态C1时从膜1中移除的对象Table 1 Objects removed from membrane 1 at configuration C1

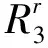
各单元格中的候选解由R6中的规则来检测。当系统处于组态C5时，如果膜1中同时存在对象fix，cjx，bkx和boxijk，这意味着数字x没有填入第i行，第j列和第k宫，因此数字x是单元格(i,j)的一个候选解。目前系统中不存在对象mijx，因此相应的三元组(i,j,x)都会触发R6中的一条规则，系统从而达到组态C6。使用集合R6中的一条规则将移除相应的对象rij，并产生对应的对象aij。由于使用R6中的规则会产生对象mijx，因此每条规则只能使用一次。

集合R6中的规则使用完毕之后，对象aij的数目意味着单元格(i,j)中候选解的个数。此时由集合R7中的规则来检测数字x是单元格(i,j)的唯一候选解：如果在使用R6中的规则后，系统中有唯一一个aij和n2-1个rij，并且单元格(i,j)为空，则单元格(i,j)有唯一候选解。除了检测唯一候选解的作用之外，集合R7中的规则将移除对象fixcjxbkx并引进对象sijx，p和w。其中对象sijx对应数独问题的解中的一个数字和一个单元格，p意味着一个新的数字填入了数独中(当p的个数达到n4个时，重启-检测循环结束)，w表示集合R7中的规则使用过一次。

在图2所示的数独中，首次使用R6中的规则后，单元格(3,7)，(5,4)，(6,1)和(7,8)对应的对象aij刚好都只有一个，这意味着这些单元格中的候选解是唯一解。因此集合R7中有4条规则被触发，物质s377、s544、s613、s788被引入到系统中，系统从而到达组态C7。

此时数独的部分解如图3所示。

图3 系统处于组态C7时对应的数独问题部分解Fig.3 Partial solution at configuration C7

使用集合R7中的规则导致组态C8中有4个对象w。其中一个w和k0一起生成对象k2(组态C8)，而其余的w将在下一步被移除(组态C9)。此时膜1中物质p的个数尚未达到n4，因此不能使用集合R10中的规则，接下来使用集合R11中的规则，物质d被移除，同时k2进化为k1，系统达到组态C10，检查阶段结束。

物质d是一个强抑制剂，没有它的存在，集合R3中的规则适用，重启阶段再次开始。系统接下来进入新的检测阶段，通过使用集合R7中的4条规则，系统中出现了s723、s448、s285、s717。这意味着4个新的数被填入数独中(系统处于组态C15时对应的数独部分解如图4所示)。

图4 系统处于组态C15时对应的数独问题部分解Fig.4 Partial solution at configuration C15

这个检测—重启循环不断进行下去，在组态C23时系统中引入了对象s174、s228、s638、s657、s742、s943、s951、s972；

组态C31时引入s237、s293、s497、s666、s692、s764、s791、s836、s867、s875、s894、s918；

组态C39时引入s262、s354、s595、s858、s965、s996；

组态C47时引入s112、s155、s168、s214、s319、s363；

组态C55时引入s126、s199、s325、s331、s398、s415、s434、s532；

组态C63时引入s421、s486、s516；

组态C71时引入s469、s561、s589。

此时膜1中的对象sijx即为数独问题的解的编码，于是数独问题的解如图5所示。

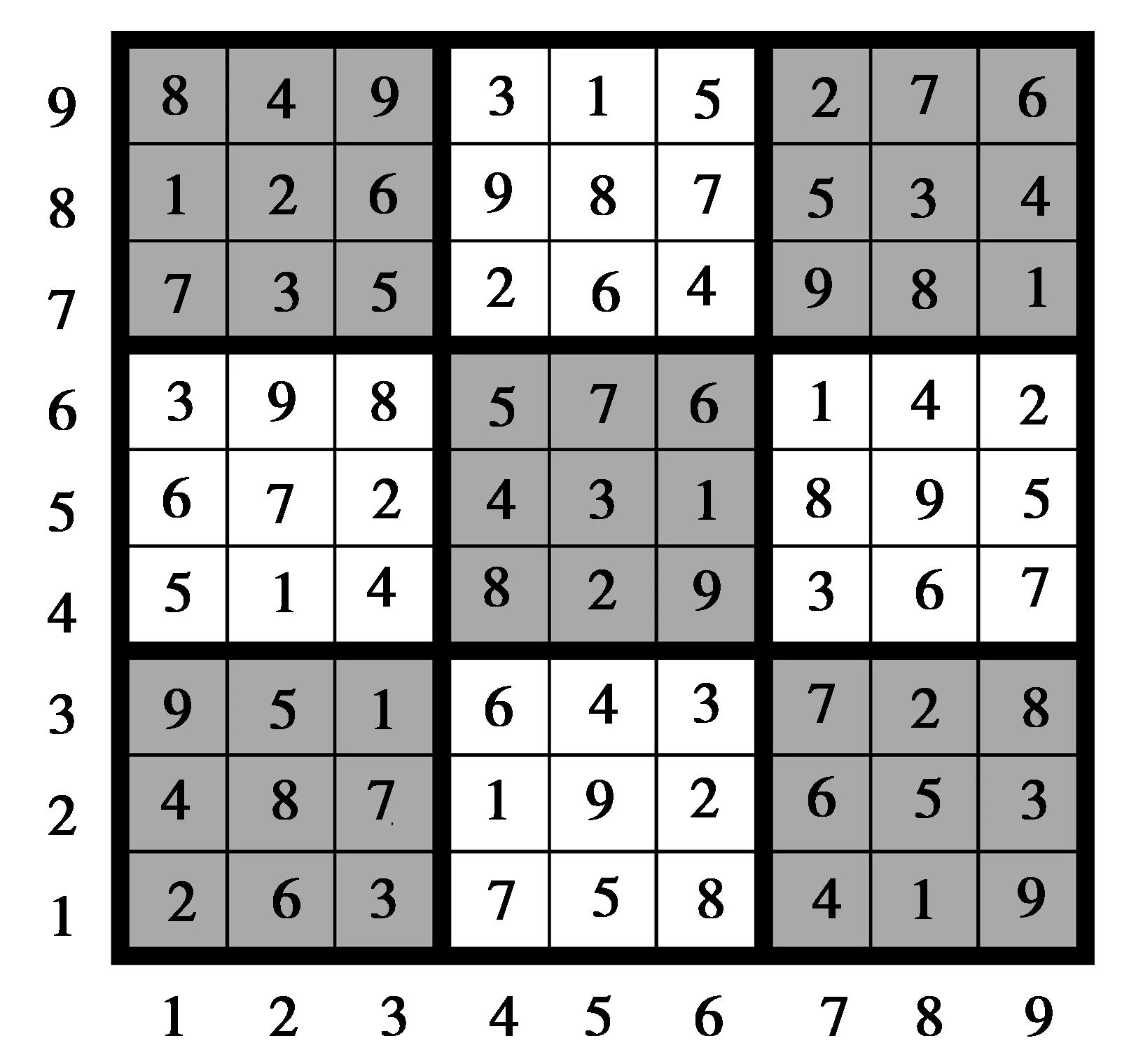
图5 数独问题的解Fig.5 Solution at configuration C71

膜系统继续计算，系统处于组态C73时膜1中有81个物质p，因此规则R10被触发，膜1溶解并且其中的所有物质进入膜0。在下一步，物质YES被送出系统，而其余对象(除sijx外)都被移除，因此当系统处于最终组态时环境中有一个物质YES以及包含解的编码的膜。

如前所述，并不是所有数独问题的所有部分解都至少包含一个具有唯一解的单元格。在这种情况下，当系统计算到达检查阶段时集合R7中没有规则可使用，于是没有物质w产生。由于系统中没有物质w，集合R8中的规则不能使用，根据规则的优先级，接下来使用集合R9中的溶解规则。随着物质NO被送入膜0，重启-检查循环结束，下一步一个物质NO被送出膜系统进入到环境中，从而计算停止。

3 结论与展望

研究了具有抑制催化、膜溶解以及规则优先级的膜系统的计算能力。对于一个数独问题，只要其所有部分解都至少包含一个具有唯一解的单元格，就可以设计出一个膜系统来进行求解，并且求解策略与人类求解数独问题的思考过程非常类似。设计的求解策略可以找到很多数独问题的解，但是并不能解决所有的数独问题。接下来可以考虑研究利用膜计算模型求解更困难的数独问题，比如因卡拉数独。

[1] FELHENHAUER B,JAVIS F.Enumerating Possible Sudoku Grids[EB/OL].http://www.shef.ac.uk/pmlafj/sudoku/sudoku.pdf

[2] YATO T,SETA T.Complexity and Completeness of Finding Another Solution and Its Application to Puzzles[J].IEICE Transactions on Fundamentals of Electronics Commu-nications and Computer Sciences,2003,E86-A(5):1052-1060

[3] CRAWFORD B,ARANDA M,CASTRO C,et al.Using Constraint Programming to Solve Sudoku Puzzles[C]∥Proceedings of the Third International Conference on Convergence and Hybrid Information Technology,2008:926-931

[4] 刘延风,刘三阳.基于遗传算法求解数独难题[J].计算机科学,2010,37(3):225-226

LIU Y F,LIU S Y.Algorithm Based on Genetic Algorithm for Sudoku Puzzles[J].Computer Science,2010,37(3):225-226

[5] 张煜东,王水花,霍元恺,等.一种基于稀疏优化的数独求解新方法[J].南京信息工程大学学报(自然科学版),2011,3(1):23-27

ZHANG Y D,WANG S H,HUO Y K,et al.A Novel Sudoku Solving Method Based on Sparse Optimization[J].Journal of Nanjing University of Information Science and Technology (Natural Science Edition),2011,3(1):23-27

[6] 商文喜,蔚承建,王开,等.数独问题的一个分布式物理博弈求解[J].计算机应用与软件,2014(12):113-115.

SHANG W X,WEI C J,WANG K,et al.A Distributed Solution of Physical Game to Sudoku Problem[J].Computer Application and Software,2014(12):113-115

[7] 陈俊.智能算法在足球机器人定向运动中的应用[J].重庆工商大学学报(自然科学版),2013,30(3):46-49

CHEN J.Application of Intelligence Algorithm to Oriented Movement of Soccer Robot[J].Journal of Chongqing Technology and Business University (Natural Science Edition),2013,30(3):46-49

[8] PAUN G.Computing with Membrane[J].Journal of Computer and System Science,2000,61(1):108-143

[9] MARTIN-VIDE C,PAUN G,PAZOS J,et al.Tissue P System[J].Theoretical Computer Science,2003,296(2):295-326

[10] IONESCU M,PAUN G,YOKOMARI T.Spiking Neural P Systems[J].Fundamenta Informaticae,2006,71(2-3):279-308

[11] PAUN G.Membrane Computing—An Introduction[M].Berlin Heidelberg:Springer-Verlag,2002

[12] CIOBANU G,PAUN G,PEREZ-JIMENEZ M J.Appli-cation of Membrane Computing[M].Berlin Heidelberg:Springer-Verlag,2006

责任编辑：田 静

Basic Solution to Sudoku Based on Membrane Computing Model

JIANG Yun

(Chongqing Engineering Laboratory for Detection, Control and Integrated System;Chongqing Technology and Business University, Chongqing 400067, China)

Sudoku problem has been proved to be an NP complete problem. In order to solve the Sudoku more efficiently, a novel approach was proposed.We designed a family of P systems using enzymatic rules, dissolution rules and priorities among sets of rules to solve a large amount of Sudokus. Results show that the strategy is effective as long as Sudokus satisfy the property that in its all partial solutions there exists at least one square with a unique candidate. If the solution can be solved by using this strategy, the P system encodes the solution and returns Yes in the last step of computation. Otherwise, the P system detects that the property is not satisfied and the computation halts by returning No. The solution is searched by using a human-style method based on looking for squares where only one candidate can be placed.Meanwhile, the solution is a uniform solution to Sudoku problem, in other words, it is irrelevant to the order of the problem and the hint numbers.

membrane computing; Sudoku; cell-like P system

2017-02-24；

2017-03-20.

国家自然科学基金项目资助(61502063).

江赟(1983-)，女，湖北红安人，讲师，博士，从事生物计算研究.

10.16055/j.issn.1672-058X.2017.0004.013

TP38

A

1672-058X(2017)04-0070-06