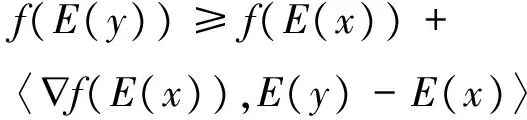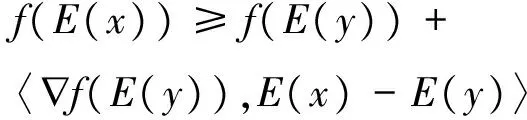广义E-凸函数的几点新发现*

李 均, 刘晓静

(1.重庆师范大学 数学科学学院,重庆 401331;2.重庆师范大学 图书馆,重庆 401331)

广义E-凸函数的几点新发现*

李 均1, 刘晓静2**

(1.重庆师范大学 数学科学学院,重庆 401331;2.重庆师范大学 图书馆,重庆 401331)

广义E-凸函数在优化理论中有着重要的作用.通过对比凸函数的相关性质，得到了广义E-凸函数与凸函数的关系，对文献[5]中引理的证明举出了反例，并对E-凸函数与E-单调的等价性给出了重新证明，进一步论证了在有限维空间中，f在特定的开集E(M)上任意一点都有上界；最后，针对广义E-凸函数已有的性质和结论进行了相应的推广.

E-凸集;E-凸函数;拟-E-凸函数;拟-半-E-凸函数;E-单调

广义凸性的研究在优化理论研究中占有十分重要的地位，E-凸函数是凸函数的推广，具有更广意义下的凸性.1999年YOUNESS[1]首先提出E-凸集和E-凸函数的概念，CHEN[2],YOUNESS[3]，郝英[4]、王蕾[5]、黄科登[6]、宁刚[7]、王建勇[8]、ZHOU等人[9]对E-凸函数的性质进行了大量的研究，并将E-凸函数推广到了半-E-凸函数、拟-半-E-凸函数.彭再云[10]、景书杰[11-12]、王世磊[13]、Beheaded[14]对广义E-凸函数的重要性质进行了研究，得到了E-凸函数等价命题等一系列重要结论.罗杰[15]率先研究E-伪凸函数性质及其应用，促进了广义E-凸函数应用的发展.基于上述研究成果，针对文献[5]中的错误引理进行了纠正，探究了E-凸函数与E-单调的等价性，得到了在特殊映射下拟-E-凸函数的等价命题，推广了文献[12]中拟-半-E-凸函数的等价形式，进一步完善了E凸性理论.

1 基本定义

定义1[1]若存在E:Rn→Rn，使得∀x,y∈M⊂Rn,∀t∈[0,1]，都满足tE(x)+(1-t)E(y)∈M，则称集合M为E-凸集.

定义2[1]若M⊂Rn为E-凸集，且存在映射E：Rn→Rn，使得对∀x,y∈M,∀t∈[0,1]，都满足f(tE(x)+(1-t)E(y))≤tf(E(x))+(1-t)f(E(y))，则称f:M⊂Rn→R为E-凸函数.

定义3[2]若M⊂Rn为E-凸集，且存在映射E：Rn→Rn，使得对∀x,y∈M,∀t∈[0,1]，都满足f(tE(x)+(1-t)E(y))≤tf(x)+(1-t)f(y)，则称f:M⊂Rn→R为半-E-凸函数.

定义4[3]若M⊂Rn为E-凸集，且存在映射E：Rn→Rn，使得对∀x,y∈M,∀t∈[0,1]，都满足f(tE(x)+(1-t)E(y))≤max{f(E(x)),f(E(y))}，则称f:M⊂Rn→R为拟-E-凸函数.

定义5[2]若M⊂Rn为E-凸集，且存在映射E：Rn→Rn，使得对∀x,y∈M,∀t∈[0,1]，都满足f(tE(x)+(1-t)E(y))≤max{f(x),f(y)}，则称f:M⊂Rn→R为拟-半-E-凸函数.

定义6[4]设非空集合M⊂Rn，f:M→R，若存在映射E:Rn→Rn，对∀x,y∈M,x≠y,都满足[E(y)-E(x)]T·[f(E(y))-f(E(x))]≥0，称f在M上E-单调.

2 主要结论及证明

定理1 设M⊂Rn为E-凸集且E(M)为凸集，则f为M上的E-凸函数当且仅当f为E(M)上的凸函数.

证明 (必要性)因为M为E-凸集，对∀x,y∈M，∀t∈[0,1]有tE(x)+(1-t)E(y)∈M且E(M)⊂M，又因为E(M)为凸集，有tE(x)+(1-t)E(y)∈E(M)⊂M，由f为M上的E-凸函数，所以有f(tE(x)+(1-t)E(y))≤tf(E(x))+(1-t)f(E(y)).因此，f为E(M)上的凸函数.

(充分性)对∀x,y∈M，有E(x),E(y)∈E(M)⊂M，由E(M)为凸集，对∀t∈[0,1]，又有tE(x)+(1-t)E(y)∈E(M)，f在E(M)上为凸函数，故f(tE(x)+(1-t)E(y))≤tf(E(x))+(1-t)f(E(y)).根据定义2，故f为M上的E-凸函数.

文献[5]中的引理为“设M为n维欧式空间Rn上的开E-凸集，f在M上具有一阶连续偏函数，则f为M上的E-凸函数的充要条件是：对任意两个不同点x,y∈M,有f(E(y))≥f(E(x))+f(E(x))T(E(y)-E(x))”.该引理存在错误，在引理的条件中并未保证E(M)为凸集，故在其充分性的证明之中，对0

例1 给定M=(0,5π)，f=sinx，f在M上显然是连续可导的，对于

下面是对文献[5]中唯一一个定理的完善，并给出了不同的证明方法.

定理2f为E-凸集M⊂Rn上可微函数且E(M)为凸集，则f为M上E-凸函数当且仅当f在M上是E-单调.

证明 (必要性)由f为M上E-凸函数，对∀x,y∈M,x≠y,∀t∈[0,1],有f(tE(x)+(1-t)E(y))≤tf(E(x))+(1-t)f(E(y)).

由E(M)为凸集，则f为E(M)上的凸函数，因为f在M上可微，则有

(1)

(2)

(充分性)f在M上可微，对∀x,y∈M且x≠y，由M是E-凸集，则E(x),E(y)∈E(M)⊂M，由均值定理可以得到f(E(y))-f(E(x))=〈f(E(ξ)),E(y)-E(x)〉.其中∃λ∈(0,1)，使得E(ξ)=E(x)+λ(E(y)-E(x)).

f(E(y))-f(E(x))=〈f(E(ξ))-f(E(x)),E(y)-E(x)〉+〈f(E(x)),E(y)-E(x)〉≥

所以f为E(M)上的凸函数，由定理1可得f为M上E-凸函数.

定理4 f:Rn→R，f为Rn上的E-凸函数，E(Rn)为开集，则∀x∈Rn，f在E(x)的邻域内有上界.

定理5 M⊂Rn为E-凸集，h:Rn→R为M拟-E-凸函数，g:R→R为非减函数，则g∘h为M上的拟-E-凸函数.

证明M为E-凸集，对∀x,y∈M,∀t∈[0,1],有tE(x)+(1-t)E(y)∈M，h为拟-E-凸函数，根据定义4,有h(tE(x)+(1-t)E(y))≤max{h(E(x)),h(E(y))}，g为非减函数，则有g∘h(tE(x)+(1-t)E(y))≤g{max{h(E(x)),h(E(y))}}=max{g∘h(E(x)),g∘h(E(y))}.

由定义4，g°h为M上的拟-E-凸函数.

推论1 若M⊂Rn为E-凸集且E(M)=M，f为拟-E-凸函数当且仅当f为M上的拟凸函数.

下面在特殊的映射E下得到了拟-E-凸函数的等价命题.

定理6 设E:Rn→Rn为线性幂等映射，则f:Rn→R为拟-E-凸函数当且仅当E-e(f)= {(x,α)∈Rn×R:f(E(x))≤α}为E×I凸集.

证明 (必要性)对∀(x1,α),(x2,α)∈E-e(f),要证E-e(f)是E×I凸集，需证∀t∈[0,1]，有t(E×I)(x1,α)+(1-t)(E×I)(x2,α)∈E-e(f),即证f(E(tE(x1)+(1-t)E(x2)))≤α，因为f为拟-E-凸函数，E为线性幂等映射，所以f(E(tE(x1)+(1-t)E(x2)))=f(tE(x1)+(1-t)E(x2))≤max{f(E(x1)),f(E(x2))}≤α,故E-e(f)为E×I凸集.

(充分性)E-e(f)为E×I凸集，设(x1,f(E(x1))),(x2,f(E(x2)))∈E-e(f)， 令α=max{f(E(x1)),f(E(x2))}.对∀t∈[0,1],有t(E×I)(x1,f(E(x1)))+(1-t)(E×I)(x2,f(E(x2)))∈E-e(f)，所以有f(tE(x1)+(1-t)E(x2))=f(E(tE(x1)+(1-t)E(x2)))≤α=max{f(E(x1)),f(E(x2))},故f为拟-E-凸函数.

定理7 若M⊂Rn为非空E-凸集，f:M→R为M上的拟凸函数，则f为M上的拟-半-E-凸函数的充要条件是对∀x∈M,都有f(E(x))≤f(x).

此定理是文献[12]中定理4的适当推广，证明类似.

[1] YOUNESS E A.E-convex Sets, E-Convex Functions, and E-Convex Programming[J].Journal of Optimization Theory and Application,1999,102(2):440-446

[2] CHEN X S.Some Properties of Semi-E-Convex Functions[J].Journal of Mathematics Analysis and Applications,2002,275:251-262

[3] YOUNESS E A.Quasi and Strictly Quasi-E-Convex Functions[J].Journal of Statistics and Management System,2001(4):201-210

[4] 郝英.一类E-凸函数及在最优化中的应用[D].天津：河北工业大学,2007

HAO Y.A Class of E-convex Function and Application in Optimization[D].Tianjin:Hebei University of Techn-ology,2007

[5] 王蕾.E-凸函数和它梯度的E-单调性的等价性证明[J].西华大学学报,2007,26(1):86-87

WANG L.The Proof on Equivalent of E-Convex Function and E-Monotonicity of Its Gradient[J]. Journal of Xihua University,2007,26(1):86-87

[6] 黄科登,马国栋.E-凸函数的拓展研究[J]. 玉林师范学院学报,2007,28(5):1-4

HUANG K D,MA G D.Extension Research of E-Convx Function[J].Journal of Yulin Normal University,2007,28(5):1-4

[7] 宁刚.E-凸函数的若干特征[J]. 运筹学学报,2007,11(1):121-126

NING G.Some Characterizations of E-convex Functions[J].Or Transactions,2007,11(1):121-126

[8] 王建勇,宋颖,白咸伦.E-拟凸函数[J].聊城大学学报,2003,16(3):16-19

WANG J Y,SONG Y,BAI X L.E-Quasiconvex Function[J].Journal of Liaocheng University,2003,16(3):16-19

[9] ZHOU M.Some New Properties of an E-Convex Function[J].Journal of Hainan Normal University,2012,25(1):5-8

[10] 彭再云.关于拟-半-E-凸函数的一个新的判别准则[J].长春师范学院学报,2006,25(1):4-5

PENG Z Y.A New Criteria of Quisi-Semi-E-convex Functions[J]. Journal of Changchun Normal University,2006,25(1):4-5

[11] 景书杰,宋虹颖.几类广义凸函数的一些新性质[J]. 聊城大学学报,2008,21(4):25-27

JING S J,SONG H Y.New Propertise of Some Kinds of Generalized Convex Functions[J]. Journal of Liaocheng University,2008,21(4):25-27

[12] 景书杰,王世磊.关于拟-半-E-凸函数的几个新结论[J].河南教育学院学报,2015,24(2):9-12

JING S J,WANG S L.Some New Conclusions of Quasi-Semi-E-Convex Function[J].Journal of Henan Institute of Education,2015,24(2):9-12

[13] 王世磊,景书杰,刘争杰.E-凸函数的一个等价定理[J].海南师范大学学报,2015,28(2):127-130

WANG S L,JING S J,LIU Z J.One Equivalent Theorem of E-Convex Functions[J]. Journal of Hainan Normal University,2015,28(2):127-130

[14] AYACHE B,KHALED S.On E-Convex and Semi-E-Convex Functions for a Linear Map E[J].Applied Mathematical Sciences,2015,9(21):1043-1049

[15] 罗杰.E-伪凸函数性质及在数学规划中的应用[J].重庆工商大学学报(自然科学版),2008,25(5):449-453

LUO J.Some Properties of E-Pseudo-Convex Functions and the Applications in Mathematical Programming[J]. Journal of Chongqing Technology and Business University (Naturnal Science Edition),2008,25(5):449-453

责任编辑：李翠薇

Some New Findings of Generalized E-Convex Function

LI Jun1, LIU Xiao-jing2

(1. School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, China;2. Library, Chongqing Normal University, Chongqing 401331, China)

The generalizedE-convex function plays an important role in the optimization theory. The relationship between generalizedE-convex function and convex function is obtained by comparing the correlation properties of convex functions. Then a counterexample is given for the proof of the lemma in the literature [5], and the equivalence between theE-convex function and theE-monotone is proved newly. It is further proved thatfhas an upper bound on a specific open setE(M) in a finite dimensional space. Finally, the properties and conclusions of the generalized E-convex function are generalized.

E-convex sets;E-convex function; quasi-E-convex function; quasi-semi-E-convex function;E-monotonicity

2016-12-22；

2017-03-15.

基础科学与前沿技术研究(重点) (cstc2015jcyjBX0029).

李均(1992-)，男，重庆人，硕士研究生，从事最优化理论研究.

**通讯作者：刘晓静(1970-)，女，四川南溪人，馆员，从事最优化理论及其在经济管理中的应用研究.

10.16055/j.issn.1672-058X.2017.0004.004

O174.13

A

1672-058X(2017)04-0020-04