带积分边值条件下分数阶脉冲微分方程解的存在性*
2017-07-18周宗福
蒋 伟, 周宗福
(安徽大学 数学科学学院,合肥 230601)
带积分边值条件下分数阶脉冲微分方程解的存在性*
蒋 伟, 周宗福**
(安徽大学 数学科学学院,合肥 230601)
针对分数阶脉冲微分方程解的存在性研究, 提出一类带积分边值条件的分数阶脉冲微分方程边值问题; 通过上下解方法, 利用Schauder 不动点定理得到此边值问题解的存在性结果; 最后给出了一个例子来说明所得结果的应用性.
积分边值条件;分数阶脉冲微分方程;Schauder不动点定理
0 引 言
近年来, 分数阶微分方程应用面十分广泛, 除了在数学各方面的应用外, 还广泛应用于生物系统的电传导、流体力学、粘弹性力学、电化学分析、分数控制系统与分数控制器等.分数阶微分方程理论吸引了很多学者研究[1-15].本文研究分数阶脉冲微分方程边值问题解的存在性. 近几年, 关于这类问题的研究可以参考文献[15-18].
在本文中,研究一类积分边值条件下的分数阶脉冲微分方程:
(1)
积分边值条件:
(2)
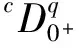
1 0=t0 J′=J{t1,t2,…tm},J0=[0,t1] Jk=(tk,tk+1],k=1,2,…,m w(t)∈C(J,J+),t-r≤w(t)≤t(t∈J),r>0 文献[19]研究了无穷区间上的分数阶微分方程积分边值问题: 文献[20]研究了如下的分数阶脉冲微分方程边值问题: 非线性边值条件: g0(u(0),u(T))=0,g1(u′(0),u′(T))=0 在以上文献的基础上,利用Schauder不动点定理讨论边值问题(1)(2)解的存在性. 定义1 函数f的q>0阶Riemann-Liouville积分定义为 定义2 函数f的q>0阶Caputo积分定义为 n-1 ② 常值函数的Caputo分数阶导数为0. 根据引理1,可以得到如下的引理. 引理3 令f(t)=L[J,R], 边值问题 (3) 的解: t∈Jk,k=0,1,2,…,m 其中, 证明 令u是式(3)的解, 由引理2,有 其中C1,C2∈R, 因此可得 如果t∈J1, 则 其中d1,d2∈R.因此有 因此 依次类推可得 t∈Jk,k=0,1,2,…,m 于是得到 证毕. 定义算子T:PC(J+)→PC(J+), 其中, 显然,T的不动点就是边值问题(1)(2)的解. 引理4 算子T是全连续的. 因此有 因此 也就意味着 所以TD一致有界. 另一方面, 对任意的u∈D,t∈Jk,0≤k≤m,有 因此, 对任意t1,t2∈Jk且t1 所以TD是全连续的,因此TD在PC(J+)上是相对紧的,所以T是全连续的.证毕. 下控制函数: 易知Ga(u),gb(u),Ya(u),yb(u),Ha(t,u,w),hb(t,u,w)关于u,w是单调不减的, 且 gb(u)≤Ik(u)≤Ga(u) hb(t,u,w)≤f(t,u,w)≤Ha(t,u,w) (t,u,w)∈[0,1]×[a,b]×[a,b] 其中, Ha(s,u(s),u(w(s)))dsdμ(τ)+ Ha(s,u(s),u(w(s)))dsdμ(τ)+ Ha(s,u(s),u(w(s)))dsdμ(τ)+ hb(s,u(s),u(w(s)))dsdμ(τ)+ hb(s,u(s),u(w(s)))dsdμ(τ)+ 下证T(S)⊂S:∀v(t)∈S, 有 下面给出一个例子说明主要结果的应用. 例1 考虑下面的边值问题: 边值条件为 由方程(5)可知其中 f(t,u,v)=2t2+cost+sinu+arctanv (6) Ha(t,u,v)=4+t+u+v hb(t,u,v)=t2+sinu+arctanv 近年来,分数阶微分方程成为研究的热点,由于其初值条件的复杂性,以及它们某些物理意义还没有得到普遍认可,所以还有大量的工作要做. 本文是研究带积分边值条件的分数阶脉冲微分方程边值问题解的存在性. 首先介绍一些定义、引理,然后定义了一个全连续算子,于是由Schauder不动点定理可知,此算子存在一个不动点,且这个不动点是边值问题的一个解. [1] AEI-SAYED A M.On the Fractional Differential Equation[J].Appl Math Comput,1992(49):205-213 [2] IBRAHIM R W,MOMANI S.On the Existence and Uniqueness of Solutions of a Class of Fractional Differential Equations[J].Math Anal Appl,2007(334):1-10 [3] TIAN Y.Differential Equations,Compute[J].Math Appl,2010(59):2601-2609 [4] PODLUBNY I.Fractional Differential Equations[M].San Diego:Academic press,1999 [5] AHMAD B,NIETO J J.Existence Results for Nonlinear Boundary Value Problems of Fractional Integro Differential Equations with Integral Boundary Conditions[J].Boundary Value Problems,2009(2009):11-19 [6] CABALLERO MENA J,HARJANI J,SADARANGANI K.Existence and Uniqueness of Positive and Nondecreasing Solutions for a Class of Singular Fractional Boundary Value Problems[J].Boundary Value Problems,2009(2009):10-20 [7] AHMAD B,NIETO J J.Existence Results for a Coupled System of Nonlinear Fractional Differential Equations with Three-Point Boundary Conditions[J].Computer and Mathematics with Applications,2009(9):1838-1843 [8] GOODRICH C S.Existence of Positive Solution to a Class of Fractional Differential Equations[J].Applied Mathematics Letters,2010(23):1050-1055 [9] ZHANG S Q.Positive Solutions to Singular Boundary Value Problem for Nonlinear Fractional Differential Equation[J].Computer and Mathematics with Applications,2010(3):1300-1309 [10] AHMAD B.Existence of Solutions for Irregular Boundary Value Problems of Nonlinear Fractional Differential Equations[J].Applied Mathematics Letters,2010(4):390-394 [11] MOMANI S,QARALLEH R.An Efficient Method for Solving Systems of Fractional Integro-Differential Equations[J].Computer and Mathematics with Applic-ations,2006(3-4):459-470 [12] HOSSEINNIA S H,RANJBAR A,MOMANI S.Using an Enhanced Homotopy Perturbation Method in Fractional Differential Equations Via Deforming the Linear Part[J].Computational and Mathematics with Applications,2008(12):3138-3149 [13] ABDULAZIZ O,HASHIM I,HOMANI S.Application of Homotopy-Perturbation Method to Fractional IVPs[J].Journal of Computational and Applied Mathematics,2008(2):574-584 [14] WANG C Y,WANG R F,WANG S,et al.Positive Solution of Singular Boundary Value Problem for a Nonlinear Fractional Differential Equation[J].Boundary Value Problems,2011(2011):12-20 [15] BAINOV D D,SIMEONOV P S.Impulsive Differential Equations,Periodic Solutions and Applications[M].New York:Longman Scientific and Technical Group Limited,1993 [16] LAKSHMIKANTHAM V,BAINOV D D,SIMEONOV P S.Theory of Impulsive Differential Equations[M].London:World Scientific and Singapore-London,1989 [17] BENCHOHRA M,HENDERVON J,NTOUYAS S K.Impulsive Differential Equations and Inclusions[M].New York:Hindawi Publishing Corporation,2006 [18] WANG J R,ZHOU Y,FECKAN M.On Recent Developments in the Theory of Boundary Value Problems for Impulsive Fractional Differential Equations[J].Computers and Mathematics with Applications,2012(64):3008-3020 [19] GUO L,ZHANG X.Existence of Positive Solutions for a Class of Fractional Differential Equations with Integral Boundary Value Condition on Infinite Interval[J].J Sys Sci Math Scis,2014(34):752-762 [20] KILBAS A A,HARIM SRIVASTAVA J,TRUJLLO J.Theory and Applications of Fractional Differential Equations[M].North-hdland Mathematics Shudies,Amsterdam:Elsevier Science B V,2006 责任编辑:李翠薇 The Existence of Solution for Impulsive Fractional Differential Equations with Integral Boundary Value Condition JIANG Wei, ZHOU Zong-fu (School of Mathematical Science, Anhui University, Hefei 230601, China) For the existence of solution to impulsive fractional differential equations, this paper proposes boundary value problems of impulsive fractional differential equations with integral boundary value condition, and the existence of solution for boundary value problems is obtained by upper and lower solutions together with Schauder fixed point theorem. Finally, an example is given to illustrate the application of the obtained results. integral boundary value condition; impulsive fractional differential equation; Schauder fixed point theorem 2016-11-23; 2017-01-17. 国家自然科学基金(11371027);安徽省自然科学基金(1608085MA12). 蒋伟(1992-),女,安徽滁州人,从事泛函微分方程的研究. **通讯作者:周宗福(1964-),男,安徽合肥人,教授,从事泛函微分方程的研究.E-mail:zhouzf12@126.com. 10.16055/j.issn.1672-058X.2017.0004.005 O175 A 1672-058X(2017)04-0024-08
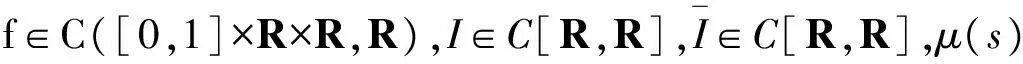
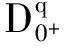
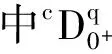
1 预备知识
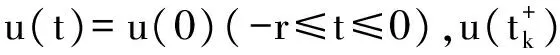
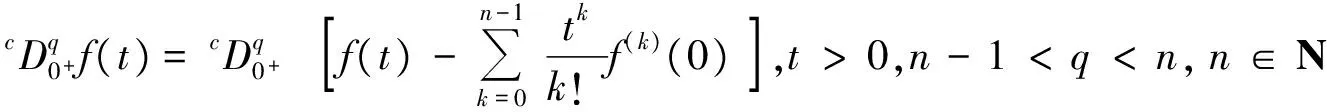
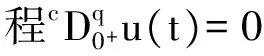
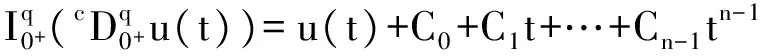

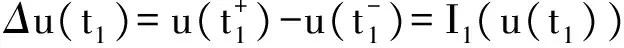
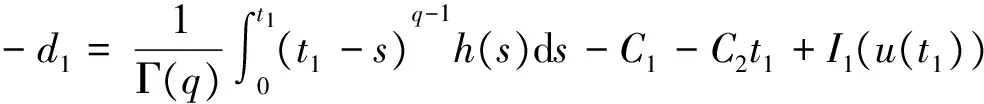
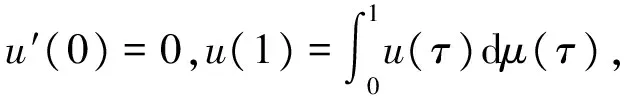
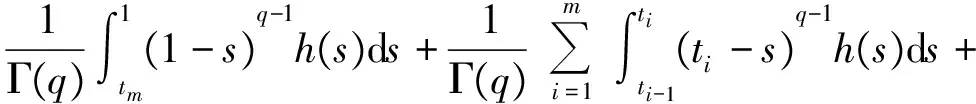


2 主要结果
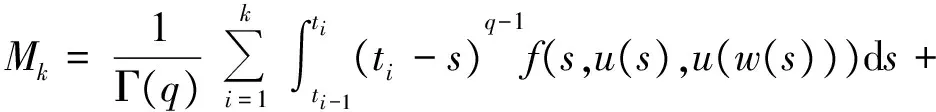
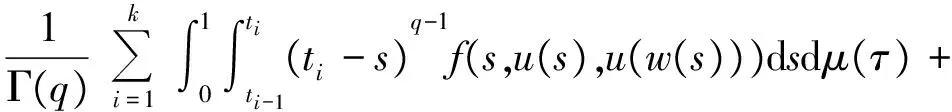
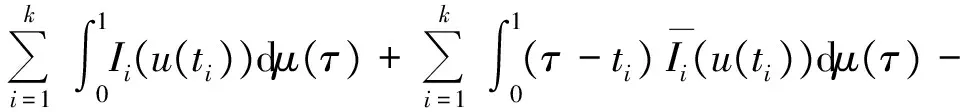
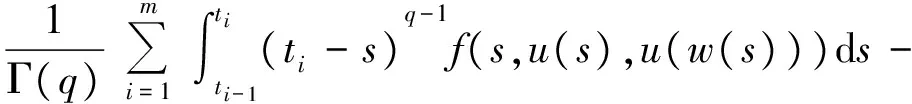
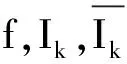
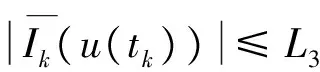
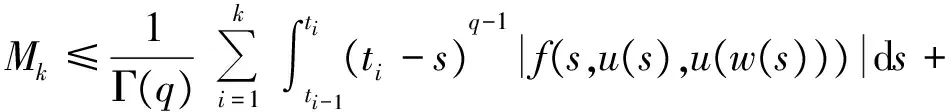
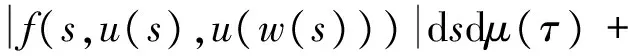
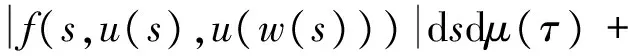
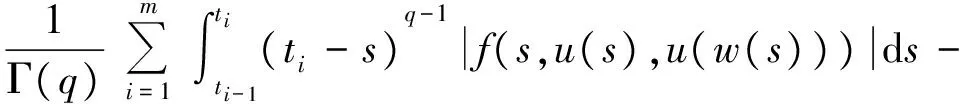
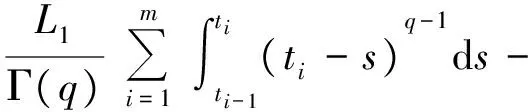
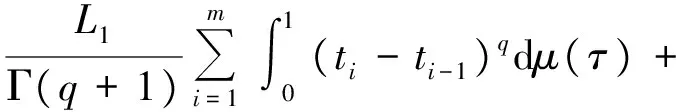
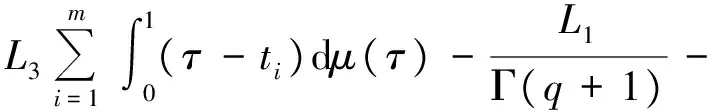

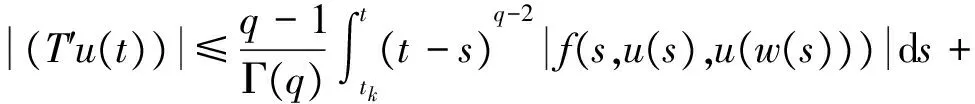
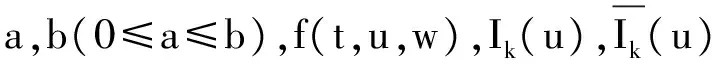
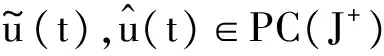

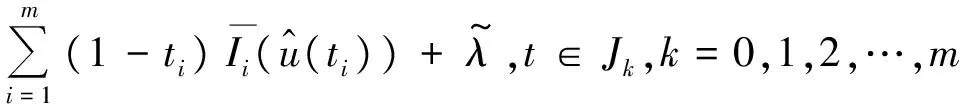
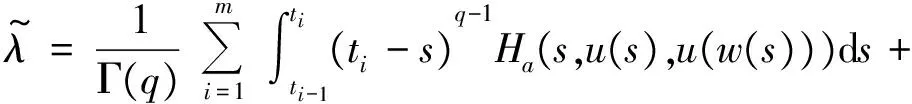
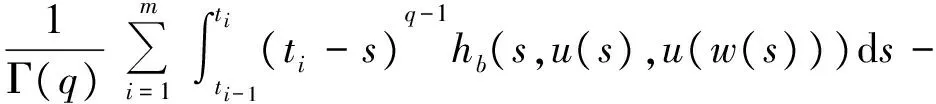
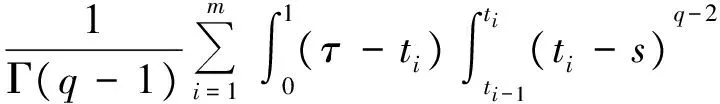

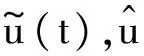
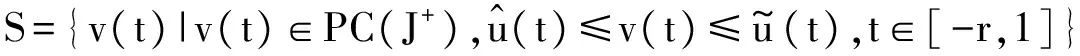

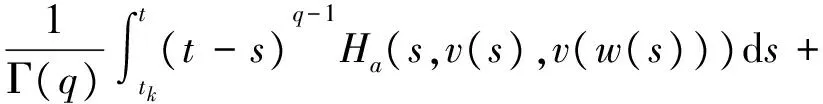
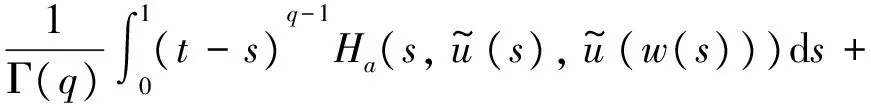
3 实例分析
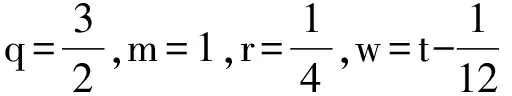
4 结 论
