关于不定方程x2+64=4yn(n=7,11)的解

尚 旭

(浙江师范大学 数理与信息工程学院，浙江 金华 321004)

关于不定方程x2+64=4yn(n=7,11)的解

尚 旭

(浙江师范大学 数理与信息工程学院，浙江 金华 321004)

不定方程整数解的问题是数论方面的一个重要分支,利用代数数论和同余的方法讨论不定方程x2+64=4yn(x,y∈Z),当n=7,11时整数解的问题,并证明了不定方程x2+64=4yn(n=7,11)无整数解.

不定方程；代数数论；整数解

设A,B∈N,A无平方因子,关于不定方程Ax2+B=Cyn,(x,y,n∈N,n≥2)解的问题是数论中的一个重要问题,用初等方法解决此类问题比较复杂和困难,近些年许多研究者用代数数论的方法研究了许多形式的不定方程.当A=1,B=1,C=1时,Ledesgue[1]证明了无整数解;Nagell[2]证明了当A=2,B=1,C=1,n=5时,仅有整数解(x,y)=(±11,3);张杰[3]证明了A=1,B=64,C=1,n=7时仅有整数解(±8，2);安晓峰[4]证明了A=1,B=64,C=1,n=11时无整数解;张四保,吕明富[5]证明了A=1,B=64,C=4,n=13时无整数解.对于A=1,B=64,C=4,n=7,11的情况未进行讨论,基于此，就此类情况进行讨论并给出了不定方程x2+64=4yn(n=7,11)无整数解的证明.

1 引理及定理证明

1.1 引理1[6-7]

设M是惟一分解整数环,正整数k≥2,以及α,β∈Z,(α,β)=1,那么若αβ=τk,τ∈M,则有α=ε1μk,β=ε2νk,μ,ν∈M,其中ε1,ε2是M中的单位元素,并且ε1ε2=εk,ε为单位元素.

1.2 定理及其证明

定理1

不定方程

x2+64=4y7,x,y∈Z

(1)

无整数解.

证明 分两种情况讨论：

(1)x≡1(mod 2),在Z[i]中,式(1)可化为(x+8i)(x-8i)=4y7(x,y∈Z).

由此和引理1，有

x+8i=4(a+bi)7,x,a,b∈Z

因此得

x=4(a7-21a5b2+35a3b4-7ab6)

(2)

8=4b(7a6-35a4b2+21a2b4-b6)

(3)

因此b=±1,±2.

当b=1时,由式(3)得

3=7(a6-5a4+3a2)

(4)

当b=-1时,由式(3)得

(5)

当b=2时,由式(3)得26+1=(7a6-140a4+336a2),即

65=7(a6-20a4+48a2)

(6)

当b=-2时,由式(3)得26-1=7(a6-20a4+48a2),整理得

9=a2(a4-20a2+48)

(7)

式(7)要成立,可知a2=1或a2=9.当a2=1,代入a2(a4-20a2+48)=29≠9,不满足.当a2=9,代入a2(a4-20a2+48)=-459≠9，不满足.所以x≡1(mod 2)时,不定方程(1)无整数解.

(2) 再讨论x≡0(mod 2)的情况,也就是x是偶数,令x=2x1,x1∈Z,此时式(1)可变为(2x1)2+64=4y7,即

(8)

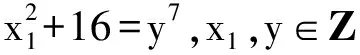
综上所述,不定方程x2+64=4y7x,y∈Z无整数解.

定理2

不定方程

(9)

无整数解.

证明 两种情况讨论：

(1) 当x≡1(mod 2)，在Z[i]中式(9)可化为(x+8i)(x-8i)=4y11(x,y∈Z).

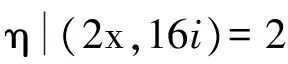
由此和引理1，有

因此有

x=4(a11-55a9b2+330a7b4-462a5b6+

165a3b8-11ab10)

(10)

8=4b(11a10-165a8b2+462a6b4-330a4b6+

55a2b8-b10)

(11)

因此b=±1,±2.

当b=1时, 由式(11)得

3=11(a10-15a8+42a6-30a4+5a2)

(12)

当b=-1时,由式(11)得

-1=11(a10-15a8+42a6-30a4+5a2)

(13)

当b=2时,由式(11)得

210+1=11(a10-60a8+672a6-

1 920a4+1 280a2)

(14)

当b=-2时,由式(11)得210-1=11(a10-60a8+672a6-1 920a4+1 280a2),即

3×31=

a2(a8-60a6+672a4-1 920a2+1 280)

(15)

显然a2=1,代入a2(a8-60a6+672a4-1 920a2+1 280)=-27≠93,所以b≠-2,所以x≡1(mod 2)时,方程(9)无整数解.

(2) 当x≡0(mod 2)时,则有x为偶数,可设x=2x1,x1∈Z，代入式(9)得:

(16)

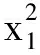
综上,不定方程x2+64=4y11x,y∈Z无整数解.

2 结 论

不定方程是数论方面的一个重要问题,在这方面的研究已经很多,本文就两个不定方程的整数解问题进行讨论,并给出这两个不定方程无整数解的结论和证明,今后希望进一步研究其他形式的不定方程的整数解问题.

[1] LEBESGUE V A.Sur Limpossibilite en Nombre Entiers de Equationxm=y2+1[J].Nouvelle Annals of Mathematics,1850,9(1):178-181

[2] NAGELL T.Sur Limpossibilite de Quelques Equations Deux Indeterminees[J].Norsk Marem Fornmings Skrefter Senel,1921,13(1):65-82

[3] 张杰.关于不定方程x2+64=y7的解的讨论[J].重庆工商大学学报(自然科学版),2012,29(3):27-28

ZHANG J.Discussion on the Solution of Diophantine Equationx2+64=y7[J].Journal of Chongqing Technology and Business University (Natural Science Edition),2012,29(3): 27-28

[4] 安晓峰.关于不定方程x2+64=y11的解的讨论[J].重庆工商大学学报(自然科学版),2014,31(10):16-17

AN X F.Discussion on the solution of Diophantine Equationx2+64=y11[J].Journal of Chongqing Technology and Business University (Natural Science Edition),2014,31 (10): 16-17

[5] 张四保,吕明富.关于不定方程x2+64=4y13的解[J].喀什师范学院学报,2010,31(3):22-23

ZHANG S,LYU M F.The Solution on Diophantine Equationx2+64=4y13[J].Journal of Kashgar Teachers College,2010,31(3):22-23

[6] 潘承洞,潘承彪.代数数论[M].2版.哈尔滨:哈尔滨工业大学出版社,2014

PAN C D,PAN C B.The Algebraic Number Theory[M].2nd edn.Harbin:Harbin Institute of Technology Press,2014

[7] 柯召,孙琦.谈谈不定方程[M].哈尔滨:哈尔滨工业大学出版社,2011

KE Z,SUN Q.About Indeterminate Equation[M].Harbin:Harbin Institute of Technology Press,2011

[8] 高丽,马永刚.关于不定方程x2+16=y7的解的讨论[J].西南民族大学学报(自然科学版),2008,34(1):27-29

GAO L,MA Y G.On Diophantine Equationx2+16=y7[J].Journal of Southwest University for Nationalities (Natural Science Edition),2008,34(1):27-29

[9] 李中恢,张四保.关于不定方程x2+16=y11的解[J].海南大学学报(自然科学版),2009,27(3):216-218

LI Z H,Z S B.Solution of the Diophantine Equationx2+16=y11[J].Journal of Hainan University (Natural Science Edition),2009,27(3):216-218

责任编辑：李翠薇

The Solution on Diophantine Equationx2+64=4yn(n=7,11)

SHANG Xu

(College of Mathematics and Information Engineering, Zhejiang Normal University, Zhejiang Jinhua 321004, China)

The integer solution to Diophantine equation is an important branch of the number theory, the problem of integer solution to the Diophantine equationx2+64=4yn(x,y∈Z) is discussed by using the methods of algebraic number theory and congruence whenn=7,11. and that the Diophantine equationx2+64=4yn(n=7,11) has no integer solution is proved.

Diophantine equation; algebraic number theory; integer solution

2016-11-10；

2016-12-12.

尚旭(1989-),男,陕西西安人,硕士研究生,从事初等数论研究.

10.16055/j.issn.1672-058X.2017.0004.006

O156.2

A

1672-058X(2017)04-0032-03