一个解可分凸优化问题的部分预校正分裂法

曾 红 秀

(重庆师范大学 数学科学学院，重庆 401331)

一个解可分凸优化问题的部分预校正分裂法

曾 红 秀

(重庆师范大学 数学科学学院，重庆 401331)

考虑线性约束的可分离凸优化问题，其目标函数可分为没有耦合变量的3个独立的凸函数.基于扩展的轮换方向乘子法，提出了一个新的解可分离凸优化问题的部分预校正分裂法，此算法在校正步中考虑对第1个变量不进行校正，对第2个和第3个变量进行校正；并且在较弱的条件下，证明了此算法的收敛性.

凸优化问题；轮换方向乘子法；部分预校正分裂法；罚参数

1 预备知识

在本文中，主要考虑如下结构型凸优化问题：

(1)

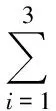
令θ:Rn→(-∞,+∞)，如果θ的域记为domθ:={x∈Rn,θ(x)<+∞}是非空的，则称θ是恰当的.如果对于任意的x∈Rn和y∈Rn，总有

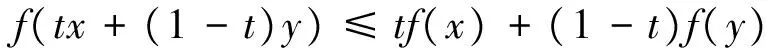
则称f是凸函数.一个集值算子T在Rn中被称为是单调的，如果满足

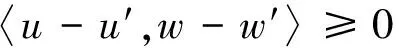
记Γ0(Rn)为下半连续恰当的凸函数从Rn到(-∞,+∞)的集合，则对于任意的θ∈Γ0(Rn)，θ是集值算子的次微分被定义为

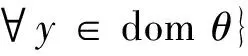
为了方便进一步的分析，令

(2)

通过引用凸优化问题的一阶最优性条件，式(1)可以很容易地被定性为下面的变分不等式问题[1]:找到一个向量u*∈U，使得

(3)

其中U:=X1×X2×X3×Rl,

因为θi(i=1,2,3)是闭凸函数，Ai(i=1,2,3)是列满秩矩阵，则式(3)是有解的[2],记式(3)为MVI(F,U),也就是说，点u*的集合满足式(3)，被记为U*,而且是非空的.

目前解决可分凸优化问题有许多有效的方法，如轮换方向法、增广拉格朗日法和预矫正邻近点法等[3-5].为了充分利用目标函数可分的特点，Gabay等[6-7]提出轮换方向乘子法,并且它在文献中已经被很广泛地的研究.轮换方向乘子法起初用于求解两个可分离变量的凸优化问题而被发展，结构如下：

x1∈X1,x2∈X2

迭代方案如下：

(4)

其中λ∈Rl是拉格朗日乘子，β>0是一个罚参数.近年来，为了进一步提高迭代步(4)的计算效率[8],研究者们将轮换方向乘子法运用到带有3个可分离变量的凸优化问题中，得到扩展的轮换方向乘子法，其迭代格式如下:

(5)

其中Lβ(x1,x2,x3,λ)是增广拉格朗日函数:

扩展的轮换方向乘子法迭代方案式(5)的数值很有前途，因此一直在图像处理和统计学习的混合正规化模型中处于中心地位[2-9].但是近几年发现在较弱的条件下，此方法的收敛性仍然是一个开放性问题，因此本文将朝着这个目标进一步发展.

2 算 法

在这一部分中，提出一个新的求解问题(1)的可分凸优化问题的部分预校正分裂法.

算法1：解可分凸优化问题的部分预校正分裂法.

(6)

步2(收敛性分析) 如果

则算法终止；否则，转步3.

(7)

令k:=k+1，返回步1.

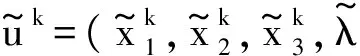
3 收敛性分析

(8)

通过在式(6)中引用凸优化问题的一阶最优性条件，可得

(9)

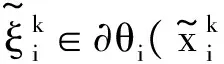
进而可以得出结论:

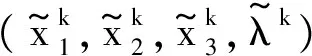
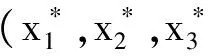
(10)

(11)

(12)

式(11)与(12)相加，得

通过F的单调性并重新排列，得

(13)

同理，可得

(14)

(15)

故结论成立.

下面3个等式明显成立：

(16)

(17)

(18)

上面3个等式(16)—(18)与式(10)相加，得

(19)

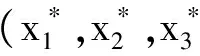
(20)

证明 由式(7)，得

(21)

以及

(22)

下面等式(23)与上述两个等式(21)(22)相加，得

(23)

可得

(24)

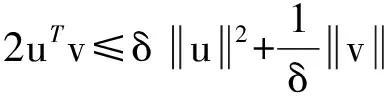
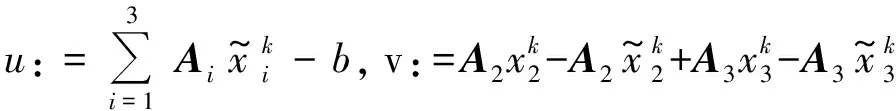
(25)

将式(25)代入式(24)中，即结论成立.

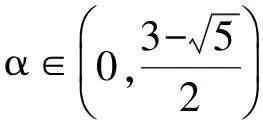
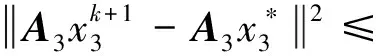
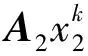
令k=0,1,…,∞相加，得

即可得

(27)

(28)

(29)

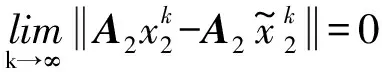
由式(3)可得

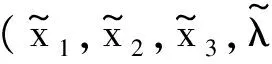
4 结 论

主要提出了一种用新的部分预校正分裂法求解3个可分离变量的凸优化问题.首先将此问题转化为求解可分离结构型变分不等式问题，基于扩展的轮换方向乘子法，进而提出了解可分离凸优化问题的部分预校正分裂法.并且在较弱的条件下，证明了新算法的全局收敛性.

[1] FACCHINEI F,PANG J.Finite-Dimensional Variational Inequalities and Complementarity Problems[M].Springer,2003

[2]TAO M,YUAN X.Recovering Low-Rank and Sparse Components of Matrices From Incomplete and Noisy Observations[J].SIAM J: Optim,2011,21:57-81

[3]AUSLENDER A,HADDOU M.An Interior Proximal Point Method for Convex Linearly Constrained Problems and Its Extention to Variational Inequalities[J].Mathematical Programming,1995,71 : 77-100

[4]YUAN X M.An Improved Proximal Alternating Direction Method for Monotone Variational Inequalities with Separable Structure[J].Computational Optimization and Applications,2011,49: 17-29

[5] 罗立.推广的预矫正邻近点法求解可分凸优化问题,重庆工商大学学报(自然科学版),2016,33(1):19-22

LUO L.Separable Convex Optimization Problem is Solved by Promoted Pre-correction Neighboring Point Method[J].Journal of Chongqing Technology and Business University (Naturnal Science Edition),2016，33(1)：19-22

[6] GABAY D,MERCIER B.A Dual Algorithm for the Solution of Nonlinear Variational Problems via Finite Element Approximations[J].Comput Math Appl,1976(2):17-40

[7] FORTIN M,GLOWINSKI R.Augmented Lagrangian Methods: Applications to the Numerical Solution of Boundary-Value Problems[J].North-Holland,1983(1):299-331

[8] BOYD S,PARIKH N,CHU E,et al.Distributed Optimi-zation and Statistical Learning via the Alternating Direction Method of Multipliers[J].Found Trends Mach Learn,2010(3):120-122

[9] NG M,YUAN X,ZHANG W.A Coupled Variational Image Decomposition and Restoration Model for Blurred Cartoon-Plus-Texture Images with Missing Pixels[J].Image Process,2013,22:2233-2246

[10] CHEN G,TEBOULLE M.A Proximal-based Decomposition Method for Convex Minimization Problems[J].Math Program,1994, 64:81-101

责任编辑：李翠薇

A Partial Prediction-correction Splitting Method for Solving Separable Convex Optimization Problems

ZENG Hong-xiu

(School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, China)

By considering the separable convex optimization problems with linear constraints, their objective function can be divided into three independent convex functions without coupling variables. Based on the extension of alternating direction of multipliers, this paper presents a new partial prediction-correction splitting method for solving separable convex optimization problems, this algorithm considers that the first variable is not corrected in correction step but the second variable and third variable are corrected. In addition, the convergence of this algorithm is proved under weaker condition.

convex optimization problem; alternating direction method of multipliers; partial prediction-correction splitting method; penalty parameter

2016-12-06；

2017-01-15.

曾红秀(1992-)，女，重庆忠县人，硕士研究生，从事最优化理论与算法研究.

10.16055/j.issn.1672-058X.2017.0004.002

O221.1

A

1672-058X(2017)04-0010-06