平面3-RRR并联机构的自激振动实验研究*

刘胜 邱志成 张宪民

(华南理工大学 广东省精密装备与制造技术重点实验室∥机械与汽车工程学院, 广东 广州 510640)

平面3-RRR并联机构的自激振动实验研究*

刘胜 邱志成 张宪民†

(华南理工大学 广东省精密装备与制造技术重点实验室∥机械与汽车工程学院, 广东 广州 510640)

从平面3-RRR并联机构的位形和关节驱动两方面,研究了位形的奇异性和驱动电机的伺服增益对机器人自激振动现象的影响.首先建立了平面3-RRR并联机构的运动约束方程,求导得到速度约束方程和加速度约束方程,给出位置、速度、加速度的正、逆解,利用速度雅可比矩阵分析奇异特性;然后搭建了实验系统,分析驱动电机的控制原理,分别测试在奇异位形和非奇异位形的自激振动,通过传感器测试驱动关节的位移、速度和加速度,并进行正解得到动平台的位置和加速度,正解得到的加速度与动平台实测加速度吻合较好;最后通过调整驱动电机的伺服增益避免了非奇异位形处的自激振动.

机器人；平面3-RRR并联机构;自激振动;奇异性;伺服系统

已有大量关于并联机器人的优化设计、运动学、标定、奇异、动力学和控制方面的研究.Tsai等[1]通过数值迭代方法求取3- PRS并联机器人的正解;Sadjadian等[2]通过人工神经网络求解冗余并联机器人的正解;Bonev等[3]利用冗余传感器的信息消除运动学正解的多解问题,得到解析解;高名旺等[4]采用运动学参数图谱的方法优化设计了一种平面3- RRR并联机器人;Liu等[5]提出了一种考虑运动和力传递特性的方法,分析了平面3- RRR并联机器人的奇异性;Huang等[6]考虑工作空间和奇异特性优化设计了平面并联3- RRR和3- RPR机器人;Agarwal等[7]提出了一种控制策略,使并联机器人在运动过程中能够避免动力学奇异位形;Pagis等[8]通过使平面并联机器人穿过第二类奇异来扩大工作空间;王锋等[9]对机械臂进行在线校准;房立金等[10]提出了一种基于量子离子群优化算法的机器人标定方法;Asier等[11]利用驱动关节的传感器信息建立了平面并联机器人的动力学模型,可实现高速、高加速度、高精度控制;Shang等[12]考虑主动关节的摩擦力影响设计了非线性控制器,用于控制平面并联机器人.

柔性机器人也是当前的研究重点之一,Wang等[13]利用拉格朗日原理和有限元法建立了柔性平面3- PRR机器人的弹性动力学模型;李渊等[14]分析了含有柔顺关节的平面并联机器人的应力;Zhang等[15]将压电陶瓷作为传感器和制动器对柔性平面3- PRR机器人的残余振动进行主动控制.

文中研究平面3- RRR并联机器人在奇异位形定位时因动平台平衡点不稳定的自激振动现象,以及在非奇异位形定位时因驱动电机的伺服增益设置不合理的自激振动现象,分析两种情况下自激振动产生的条件和原因,通过调整驱动电机的伺服增益以避免非奇异位形处的自激振动.

1 平面3- RRR并联机构的运动学分析

图1为平面3-RRR并联机构示意图,运动学参数如下:固定平台AiO(i=1,2,3)尺寸为0.4 m,主动杆AiBi长为0.245 m,被动杆BiCi长为0.242 m,动平台CiP尺寸为0.112 m.主动关节A1、A2和A3呈等边三角形分布,3条支链对称分布.以固定平台A1A2A3的中心为原点建立坐标系,X轴与A1A2平行,Y轴与A1A2垂直,动平台中心点P的位置(x,y)和姿态转角qc为机构的输出,主动关节的角度(qa1,qa2,qa3)为机构的输入.

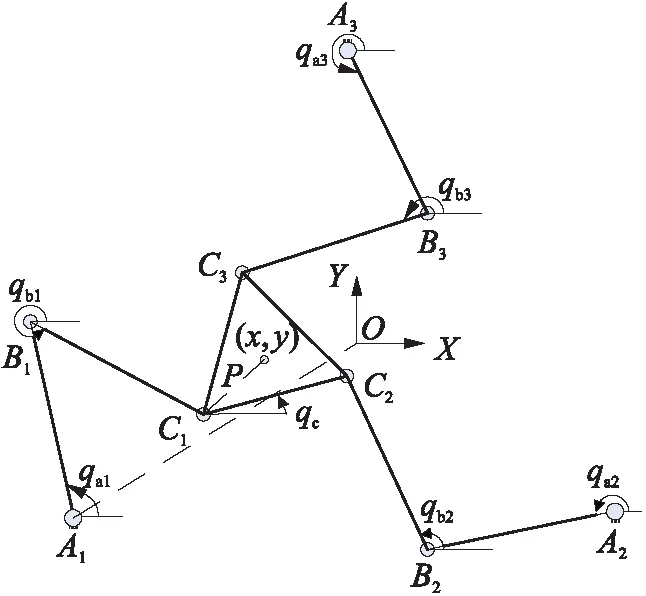
图1 平面3-RRR并联机构示意图

用带有封闭链向量的几何方法来描述平面3-RRR并联机构的运动学,满足运动约束关系:

(1)

将矢量方程(1)投影到X轴和Y轴方向,对时间求导得到速度约束方程:

diag{l1sin(qb1-qa1),l1sin(qb2-qa2),

(2)

式中,l1为主动杆长，l3为动平台中心到顶点的距离.

将方程组表示为向量矩阵形式:

(3)

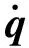
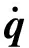
(4)

加速度逆解的求取方法为:先通过位置逆解得到输入位置,再通过速度逆解得到输入速度,最后通过加速度逆解得到输入加速度,即

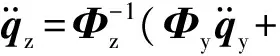
(5)

加速度正解的求取方法为:先通过位置正解得到输出位置,再通过速度正解得到输出速度,最后通过加速度正解得到输出加速度,即

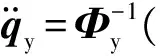
(6)

2 平面3- RRR并联机器人实验系统

本实验系统实物图如图2所示,大理石基座、钢架结构和钢板组成固定平台,3台三相交流伺服电机安装在固定平台上,经过减速器驱动主动关节.使用型号为SGMAV- 10ADA61的伺服电机和型号为SGDV- 120A的伺服驱动器(安川电机有限公司),20位的增量式编码器测试主动关节的位置和速度,采用型号为VRS- 075B- 5-K3- 19DC19的减速器(广东新宝电器股份有限公司,减速比为1∶5)和德国Dspace公司的DS1103半物理仿真控制卡.在位置控制模式下,控制卡发送数字脉冲信号给伺服驱动器,伺服驱动器完成电流闭环、速度闭环和位置闭环的控制算法.在力矩控制模式下,控制卡发送模拟电压信号给伺服驱动器,控制卡完成速度闭环和位置闭环的控制算法.文中实验是在位置控制模式下进行的.如图3所示,在距离驱动关节0.18m的中心安装单自由度加速度传感器,选用型号为222A50的加速度传感器(扬州英迈克测控技术有限公司)检测主动杆转动方向加速度.2个三自由度加速度传感器安装在动平台的中心和Y轴正方向距离动平台中心0.052 m的位置,选用型号为243A10的加速度传感器检测动平台3个方向的加速度.加速度传感器信号经过电荷放大器YE5850转换为电压信号.

图2 实验系统实物图

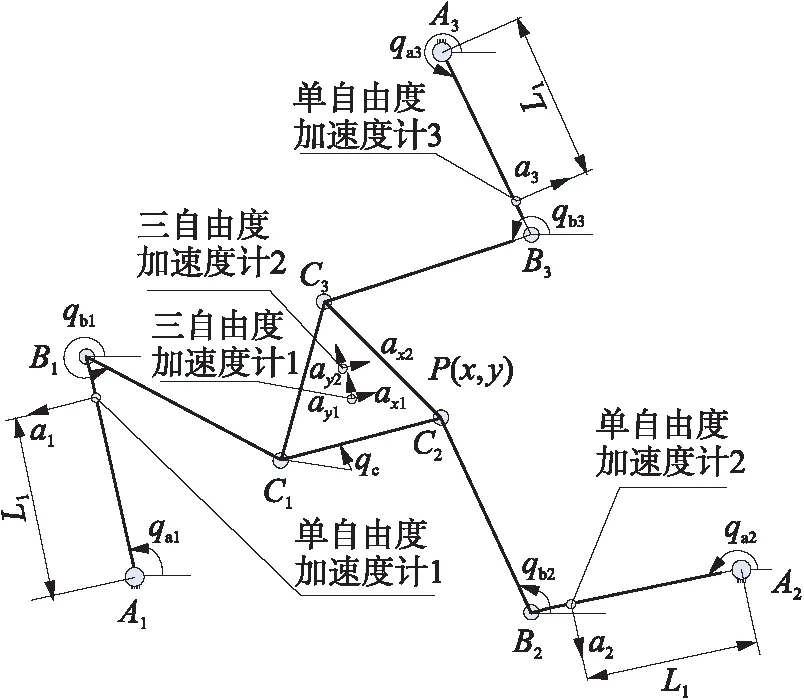
图3 加速度传感器的安装示意图

Fig.3 Schematic diagram of installation of acceleration sensors

3 自激振动的实验研究

3.1 奇异位形定位时的自激振动

位形(0 mm,0 mm,-38°)如图4(a)所示,3条被动杆的延长线交于一点;图4(b)给出了-38°定姿态工作空间内正向雅可比矩阵行列式det(Φy)的分布,其中虚线为工作空间边界,实线为det(Φy)的等高线,中间区域为奇异位形,det(Φy)为0.

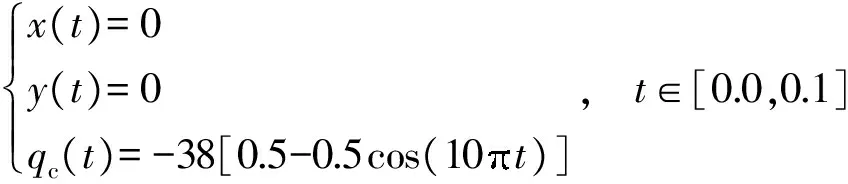
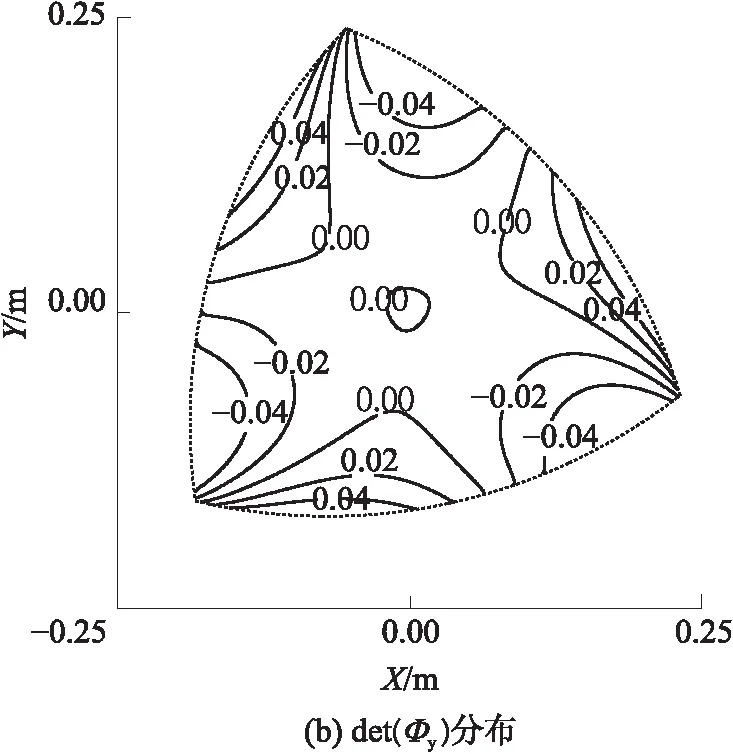
图4 奇异位形示意图与det(Φy)

Fig.4 Schematic diagram of singular configuration and distribution of det(Φy)

(7)

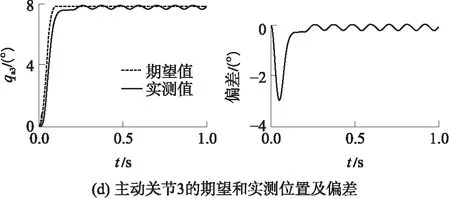
图5 奇异位形的自激振动

动平台在正向奇异位形附近摆动,det(Φy)在0附近上下摆动.在奇异位形附近,平面3- RRR并联机构的驱动关节位置有2个动平台位置与之对应,机构输入有2个运动学正解,驱动关节的位置无法唯一确定动平台的位形,使得动平台的位形不稳定,会左右摆动,动平台摆动带动驱动关节自激振动.这种自激振动是由奇异位形定位不稳定引起的.

3.2 非奇异位形定位时的自激振动

(8)

主动关节的期望轨迹和实测轨迹如图6(b)所示,在期望轨迹完成后,驱动电机进入自激振动状态.图6(c)为主动关节的轨迹跟踪误差,完成期望轨迹后出现稳定的正弦规律误差,主动关节表现为自激振动.

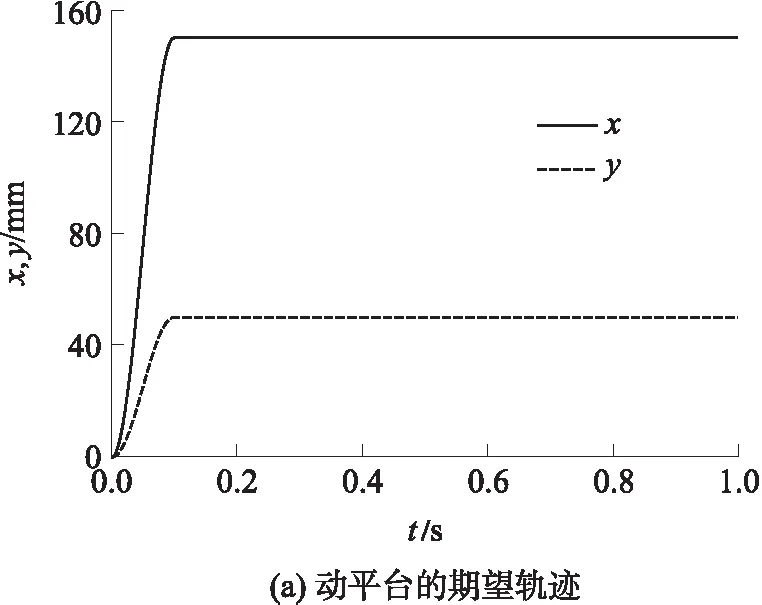
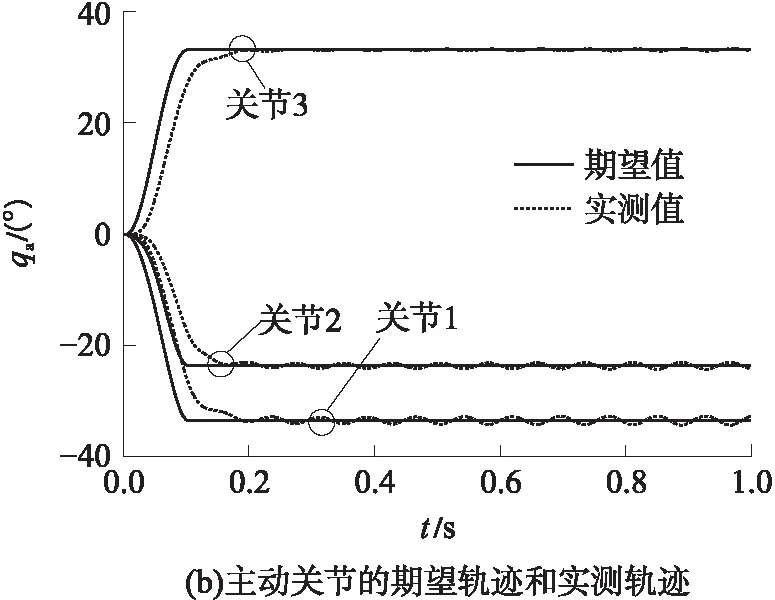
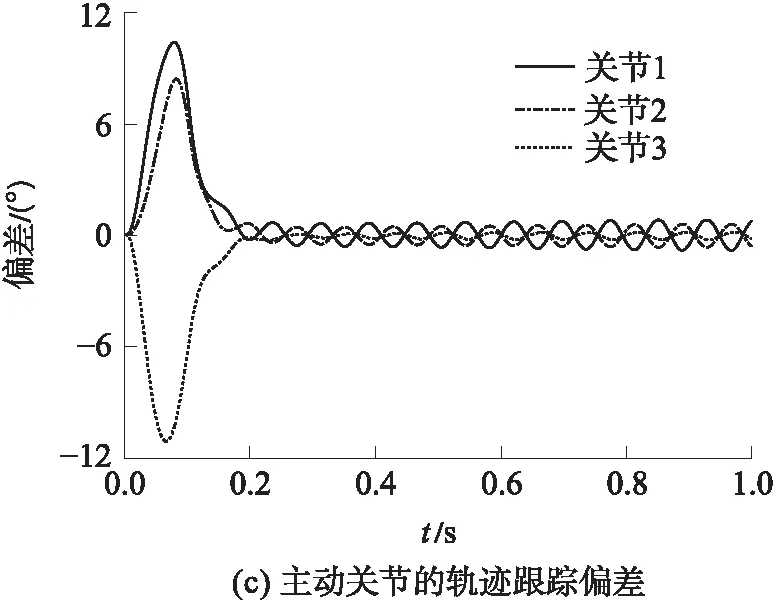
图6 非奇异位形的自激振动

图7为自激振动时(0.6～0.8 s时间段)3条主动杆的加速度信号，其中a为加速度，f为频率.3个加速度主要为12.70 Hz信号,主动关节3的加速度有较强的26.37 Hz信号.

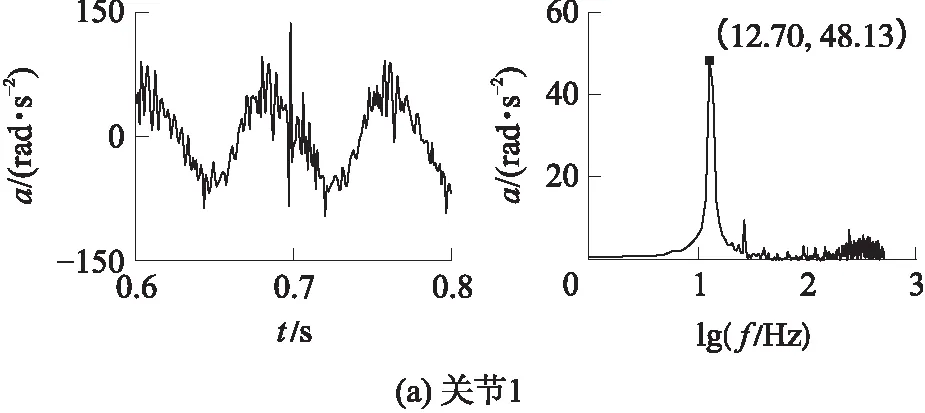
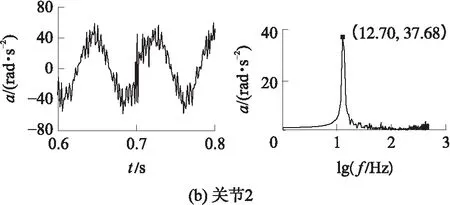
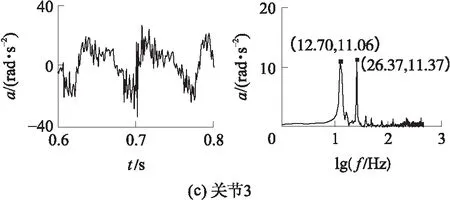
图7 主动关节在时域和频域的实测加速度

Fig.7 Experimental acceleration of active joints in time domain and frequency domain

由实测的主动关节位置,通过正解得到动平台位置,如图8所示,动平台表现为自激振动.

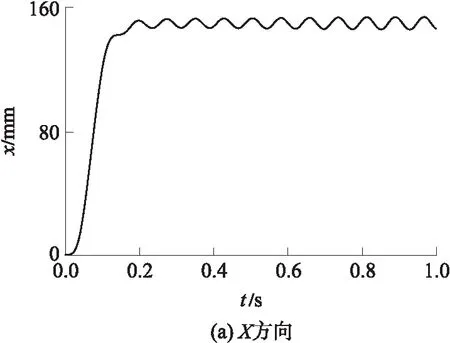
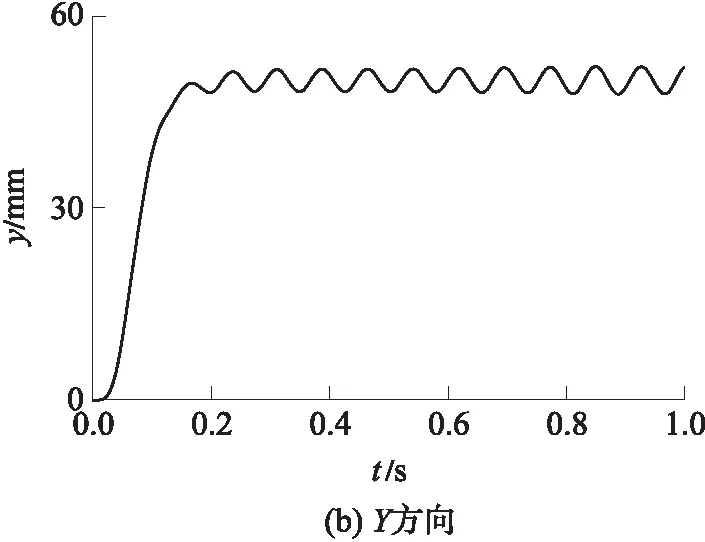
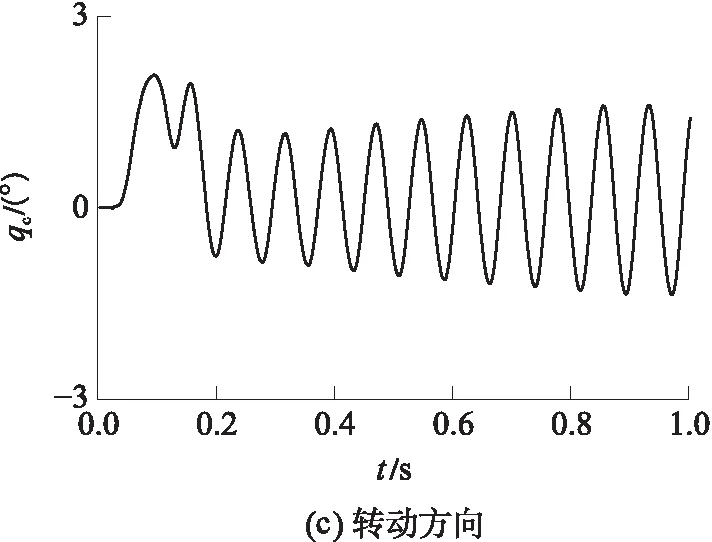
图8 运动学正解得到的动平台位置

Fig.8 Position of the moving platform through forward kinematic

由主动关节的实测位置、速度和加速度,通过正解得到动平台加速度如图9所示,主要为12.70 Hz信号.图10为实测的动平台加速度,主要为12.70 Hz信号,Y方向加速度有49.80 Hz信号.

图11为由实测的主动关节位置、速度、加速度通过正解得到的动平台加速度和动平台实测加速度.

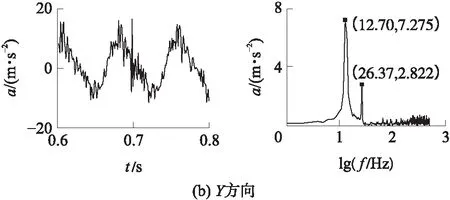
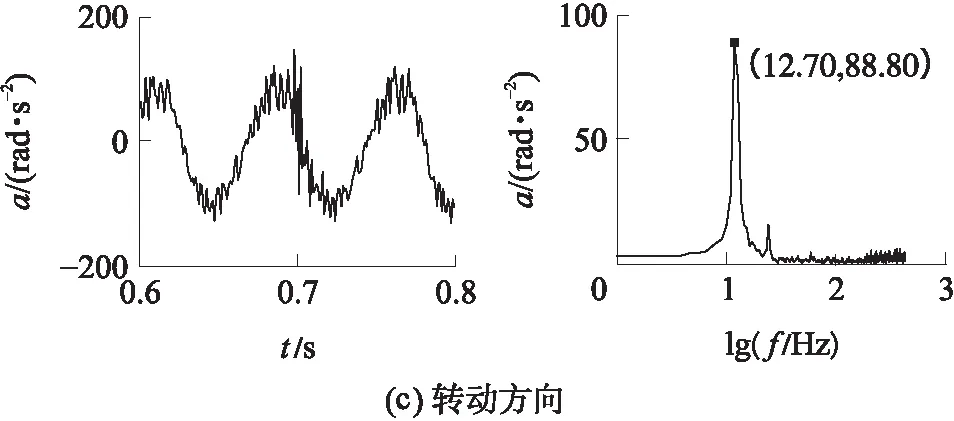
图9 运动学正解得到的动平台加速度

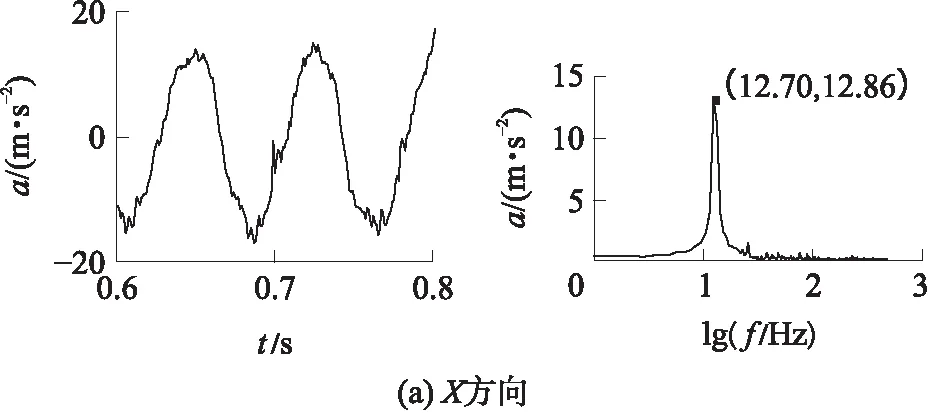
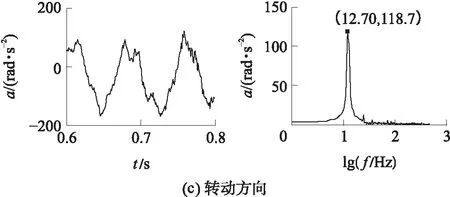
图10 加速度传感器实测的动平台加速度

Fig.10 Acceleration of the moving platform through accelero-meters sensors

从图9-11可以看出:除了高频干扰外,两种动平台的加速度在时域和频域内吻合较好;在自激振

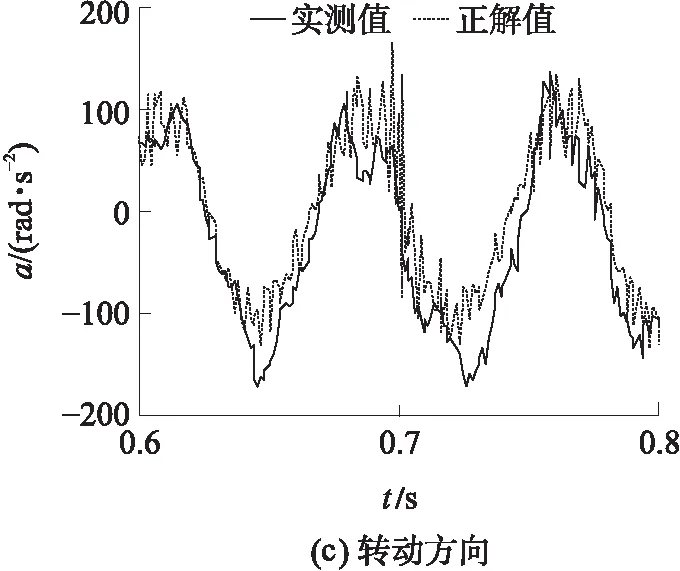
图11 两种动平台加速度

动状态下,主动关节实测位置、速度、加速度和动平台实测加速度符合运动学约束方程,说明非奇异位形下的自激振动是单纯的驱动电机振动.因为伺服电机的伺服增益设置偏大,伺服电机在期望位置上下波动,故可通过减小伺服增益来避免这种自激振动.

3.3 非奇异位形定位时自激振动的避免

图12为驱动电机的伺服控制系统结构框图,伺服电机的伺服增益包括多个参数,如：速度控制环增益、位置控制环增益、滤波器参数、摩擦补偿参数、转动惯量参数等.

选择机器人初始位形(0 mm,0 mm,0°)和非奇异位形(150 mm,50 mm,0°)为起点和终点,实验条件与前面一致,降低伺服控制系统的伺服增益,实验结果如图13所示,在运动过程中虽然主动关节的轨迹跟踪偏差较大,但无自激振动.伺服电机在伺服增益较大时容易引起自激振动现象,而在伺服增益较小时不容易引起自激振动现象,因此在非奇异位形定位时适当减小伺服增益，可以避免伺服电机产生自激振动.

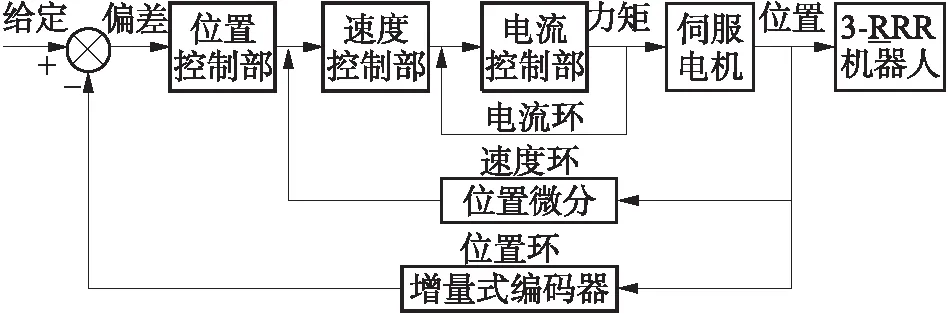
图12 驱动电机的伺服控制系统结构

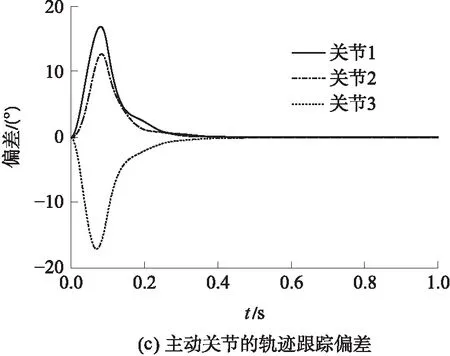
图13 避免自激振动实验结果

4 结论

文中建立了平面3- RRR并联机构的运动学方程,搭建了其实验系统,通过3组定位实验对平面3- RRR并联机构的自激振动现象进行研究,得到以下结论:

(1)平面3- RRR并联机构存在两种情况下的自激振动现象,第一种是在正向雅可比矩阵奇异位形定位时因动平台平衡点不稳定的自激振动现象,此时驱动关节无法控制动平台;第二种是在非奇异位形定位时因驱动电机的伺服增益设置过大的自激振动现象.

(2)在非奇异位形且驱动电机的伺服增益设置较大时,驱动电机会出现稳态误差而自激振动,从而引起动平台自激振动.驱动电机的位置、速度、加速度和动平台的加速度符合刚体运动学约束方程.调整伺服电机控制系统的伺服增益,可以避免定位时的自激振动.

[1] TSAI M S,SHIAU T N,TSAI Y J,et al.Direct kinematic analysis of a 3-PRS parallel mechanism [J].Mechanism and Machine Theory,2003,38(1):71- 83.

[2] SADJADIAN H,TAGHIRAD H D.Comparison of different methods for computing the forward kinematics of a redundant parallel manipulator [J].Journal of Intelligent and Robotic Systems,2005,44(3):225- 246.

[3] BONEV I A,RYU J,KIM S G,et al.A closed-form solution to the direct kinematics of nearly general parallel manipulators with optimally located three linear extra sensors [J].IEEE Transactions on Robotics and Automation,2001,17(2):148- 156.

[4] 高名旺,张宪民,刘晗.3- RRR高速并联机器人运动学设计与实验 [J].机器人,2013,35(6):716- 722. GAO Ming-wang,ZHANG Xian-min,LIU Han.Experiment and kinematic design of 3- RRR parallel robot with high speed [J].Robot,2013,35(6):716- 722.

[5] LIU Xin-jun,WU Chao,Wang Jin-song.A new approach for singularity analysis and closeness measurement to singularities of parallel manipulators [J].Journal of Mechanisms and Robotics,2012,4(4):1- 10.

[6] HUANG M Z,THEBERT J.A study of workspace and sin-

gularity characteristics for design of 3- DOF planar parallel robots [J].The International Journal of Advanced Manufacturing Technology,2010,51(5/6/7/8):789- 797.

[7] AGARWAL A,NASA C,BANDYOPADHYAY S.Dyna-mic singularity avoidance for parallel manipulators using a task-priority based control scheme [J].Mechanism and Machine Theory,2016,96:107- 126.

[8] PAGIS G,BOUTON N,BRIOT S,et al.Enlarging parallel robot workspace through type- 2 singularity crossing [J].Control Engineering Practice,2015,39:1- 11.

[9] 王锋,陈凯,陈小平.一种含间隙机械臂的在线校准方法 [J].机器人,2013,35(5):522- 526. WANG Feng,CHEN Kai,CHEN Xiao-ping.An online calibration method for manipulator with joint clearance [J].Robot,2013,13(5):521- 526.

[10] 房立金,党鹏飞.基于量子离子群优化算法的机器人运动学标定方法 [J].机械工程学报,2016,52(7):23- 29. FANG Li-jin,DANG Peng-fei.Kinematic calibration me-thod of robots based on quantum-behaved particle swarm optimization [J].Journal of Mechanical Engineering,2016,52(7):23- 29.

[11] ASIER Z,ITZIAR C,MARGA M.Dynamic modeling of planar parallel robots considering passive joint sensor data [J].Robotic,2010,28:649- 661.

[12] SHANG Wei-wei,CONG Shuang,JIANG Shi-long.Dynamic model based nonlinear tracking control of a planar parallel manipulator [J].Nonlinear Dynamics,2010,6(4):597- 606.

[13] WANG Xiao-yun,MILLS J K.Dynamic modeling of a flexible-link planar parallel platform using a substructuring approach [J].Mechanism and Machine Theory,2006,41(6):671- 687.

[14] 李渊,余跃庆.含有柔顺关节的并联机器人应力分析 [J].北京工业大学学报,2016,42(6):832- 836. LI Yuan,YU Yue-qing.Stress analysis of parallel robots with compliant joints [J].Journal of Beijing University of Technology,2016,42(6):832- 836.

[15] ZHANG Xu-ping,MILLS J K,CLEGHORN W L.Experimental implementation on vibration mode control of a moving 3-PRR flexible parallel manipulator with multiple PZT transducers [J].Journal of Vibration and Control,2010,16(13):2035- 2054.

Experimental Investigation into Self-Excited Vibration of a Planar 3-RRR Parallel Manipulator

LIUShengQIUZhi-chengZHANGXian-min

(Guangdong Province Key Laboratory of Precision Equipment and Manufacturing Technology∥School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China)

Dealt with in this paper are the effects of singularity configuration and servo gain of drive motors on the self-excited vibration of planar 3-RRR parallel manipulator. Firstly, the kinematics constraint equation of the planar 3-RRR parallel manipulator was established, and the velocity constraint equation as well as the acceleration constraint equation was obtained via derivation. Meanwhile, the forward and inverse solutions of position, velocity and acceleration are analyzed. Secondly, the singularity was measured by using the velocity Jacobin matrix. Then, an experimental system was established to test the self-excited vibration respectively in singular and non-singular configurations after analyzing the control principle of drive motors. Moreover, the input position, velocity and acceleration of active joints were tested by sensors, the position and acceleration of the moving platform were obtained via forward kinematics, and the obtained acceleration of the moving platform accord with the test one well. Finally, the self-excited vibration in non-singular configurations was successfully avoided by adjusting the servo gain of drive motors.

robot;planar 3-RRR parallel manipulator; self-excited vibration; singularity; servo systems

2016- 07- 15

NSFC-广东省自然科学联合基金资助项目(U1501247);东莞市重大科技项目(2015215119) Foundation item: Supported by the Joint Fund of the National Natural Science Foundation and the Guandong Provincial Natural Science Foundation(U1501247)

刘胜(1986-),男,博士生,主要从事并联机器人控制研究.E-mail:liusheng20080818@163.com

†通信作者: 张宪民(1964-),男,教授,博士生导师,主要从事机构学、精密制造装备与现代化控制技术研究.E-mail:zhangxm@scut.edu.cn

1000- 565X(2017)05- 0024- 07

TP 271+.4

10.3969/j.issn.1000-565X.2017.05.004