“高等数学”课程的多重教学方法效果比较分析

边家文,杨迪威,付丽华,李宏伟

(中国地质大学 数理学院，湖北 武汉 430074)

“高等数学”课程的多重教学方法效果比较分析

边家文,杨迪威,付丽华,李宏伟

(中国地质大学 数理学院，湖北 武汉 430074)

以“高等数学”课程为例，对课程中引入研究性学习、翻转课堂和MOOCs 3种单一以及3重教学方法的可行性方案进行了探讨和比较分析，并对实施效果从兴趣、成绩、知识面、独立思考能力以及学习习惯5个方面进行了比较分析.

高等数学课程； 多重教学方法； 研究性学习； 翻转课堂； MOOCs

随着计算机以及信息技术的不断发展以及教学手段的日益多样化，出现了研究性学习[1]、翻转课堂[2]和MOOCs[3]等多种新教学方法，这些新教学方法均从某个方面克服了传统教学方法在某些方面的不足之处.研究性教学方式是指在教育教学中，支持学生主动思考、主动探究和主动实践，以培养学生自主创新能力为目的一种教学理念和教学模式，着眼于学习方式的转变，强调以学生为中心，自由选题、自主探究和自由创造为宗旨，推动学生不断迈向创造性.翻转课堂是一种混合使用技术和亲自动手活动的教学环境.在翻转课堂中，典型的课堂讲解时间由实验和课内讨论等活动代替，而课堂讲解则以视频等其他媒介形式由学生在课外活动时间完成[4].MOOCs(Massive Open Online Courses)中文直译为大规模开放在线课程，最早由2008 年由加拿大的Cormier D和美国的Alexander B 2位学者首次提出，之后MOOCs迅速成为网络课程学习的新潮流，影响几乎遍及了大学的所有学科[5].以上3种方法尽管在实施方式上存在较大差别，但具有一定的相似之处，3种方法均强调学生的主动学习.MOOCs和翻转课堂均需要学生对进行网络课程的学习，研究性学习和翻转课堂则强调在实践和讨论中进行学习.

以“高等数学”课程为例，对3种教学方法进行单一实践以及3重教学方法实践，从兴趣、成绩、知识面、独立思考能力以及学习习惯5个方面对4种情形下的实施效果进行统计评价与分析，利用聚类分析对4种情形下各个评价指标之间的相关关系进行分类和相关分析，最后利用总体假设检验，方差齐性检验以及总体均值的逐对总体假设检验分析了4种情形下教学效果差异.

1 “高等数学”课程的多重教学方法改革尝试

近年来，研究性学习、翻转课堂以及MOOCs 3种教学方法在多个学科领域的教学中取得了一定的成功.相对一般课程，“高等数学”课程具备理论性强、连贯性强以及系统性强的特点，如何在合适的教学环节中引入3种教学方法，克服“高等数学”课程教学的难点以及弥补传统教学方法的被动式教学的不足值得进行深入研究.

1.1 基于研究性学习的实践与探索 基于研究性学习的教学模式是指在教育教学中，支持学生主动思考、主动探究、主动实践，以培养学生自主创新能力为目的的一种教学理念和教学模式，着眼于学习方式的转变，强调以学生为中心，以自由选题、自主探究和自由创造为宗旨，推动学生不断迈向创造性.研究性学习强调以问题为导向，在真实的情境中使学生的好奇心驱动其自主探究，在解决问题的过程中积累经验、学会思考[6].另外，研究性学习强调在教师指导下学生以个人或小组协作的方式进行自主学习，使学生成为自己学习的真正主人.研究性学习有助于学生主动学习，牢固掌握知识，有助于学生从练习中获取知识的真谛.目前，国内外对于本科工程教育研究性教学进行了一系列的探索与实践，包括美国的发现法、讨论法和程序教学法，前苏联的分步探索法和问题讨论法以及西德的范例教学法等；我国一批研究型大学纷纷开始进行本科工程教育研究性教学的实践探索，并取得了初步成功，包括清华大学的大学生研究训练计划(SRT)和浙江大学的大学生科研训练计划(SRTP)等.随后，其他各高校也纷纷在《国家中长期教育改革和发展规划纲要》[7]、《教育部关于实施“卓越工程师教育培养计划”的若干意见》[8]和《教育部等部门关于进一步加强高校实践育人工作的若干意见》[9]等一系列文件的倡导下，展开了形式各异的本科工程教育研究性教学探索与实践.

通过研究性学习的特点和发展过程可见，工程教育由于具备大量的实践教学素材，十分便于研究性学习的开展，能否将研究性学习方法运用于“高等数学”等理科课程的教学值得进行探索与研究.事实上，研究性学习的最大的特点是基于问题的探究式学习方式，对于“高等数学”课程而言，可以借鉴研究性学习的学习方式从以下几个方面开展研究性学习的教学：1)基于课程相关或相似概念的分组讨论以及实例说明，加深对于数学抽象概念的理解和掌握.对于“高等数学”课程，可以开展概念的分组讨论以及实例说明的内容包括：一元和多元函数的连续、可导与可微、极限与级数收敛、积分与可导、定积分与不定积分以及无穷积分与瑕积分之间的相关关系等.对于小组讨论结果，教师进行适度评价与修正.2)基于一题多解的课外练习.一题多解与研究性学习的本质具有一定的相似之处，即可以让学生在已掌握的理论框架下展开自由思考和探索的空间，帮助学生养成主动思考问题、解决问题的习惯，培养学习兴趣.“高等数学”课程包含十分丰富的一题多解的知识点，比如对于极限的计算、不定积分和定积分的计算可以利用不同的换元技巧进行计算；二重积分和三重积分的计算可以在不同的坐标系下进行求解；无穷级数部分的正项级数往往存在多个收敛判别方法等.教师在平时习题的讲解中也要引导学生进行多个方法的思考与求解.3)进行理论与实验结合、图形结合的课外练习活动，增强对数学课程的直观认识.“高等数学”课程中很多内容均可以进行数学实验得到和书本相同的理论结果或图像描绘，开展数学实验的课外练习活动有利于增强学生对数学的直观认识、提升对数学课程的学习兴趣以及对数学知识的应用能力.比如对于极限的计算，学生可以通过Matlab编程观察自变量变化过程中函数值的变化趋势；对于空间曲线和曲面，学生可以利用Matlab画图软件得到曲线和曲面方程对应的图像并通过手动模仿增强对于这些空间几何图像的认知，有利于重积分部分积分区域图像的绘制；对于多元函数的最值问题，学生可以借助二分法、梯度下降法或遗传算法等优化方法实现对于多元函数最值的数值求解.4)利用和借鉴数学建模中半开放性问题让学生进行大胆思维和探索.比如对于2016年的全国大学生数学建模竞赛A题中的钢桶状态问题，可以仅仅让学生考虑水流静止，风力水平情形下的钢桶姿态问题，通过该问题的求解使得学生熟悉和掌握优化算法、多方案的评价方法，提高学生应用数学解决实际问题的能力.

1.2 基于翻转课堂的学习与实践 翻转课堂是一种混合使用技术和亲自动手活动的教学环境，典型的课堂讲解时间由实验和课内讨论等活动代替，课堂讲解则以视频等其他媒介形式由学生在课外活动时间完成[9].翻转课堂由孟加拉裔美国人萨尔曼·汗提出.2006年11月萨尔曼·汗在YouTube网站发布了自己制作的第一个教学视频，并很快引起了关注，目前YouTube网站上放置了3 000多段的免费视频课程，有超过6 000万人次通过网络参与其课程学习.

传统的课堂教学，学习过程主要以教师为中心，使用传授课程内容的讲授模式，学生是一种被动学习的角色.在翻转课堂中，学生在课堂上以课内作业、实验和讨论的形式参与学习活动，利用相互解释概念的优点达到强化、巩固其对这些概念的理解.从积极学习对比消极学习的角度来看，翻转课堂模式起到了将消极学习从课堂中抽离，将其推向家庭、图书馆或其他时间，把积极学习推向课堂，值得传统讲授式课堂进行借鉴和改进.

对于“高等数学“课程，由于其理论的深度和学生知识面的局限性，不适合将整个课程实行翻转课堂的实践，一些较难的知识点仅仅通过视频学习或学生之间的讨论仍然难以理解，需要师生之间的多次互动以及教师实时的观察调整和多次的强调加以理解和消化.难度较小的部分，学生在掌握基本概念和定理后通过视频学习再辅以课堂讨论，学生是完全可以理解、掌握且学习效果相对于传统的课堂数学更加容易被学生内化吸收.为了提高学生学习效率，可以按照以下步骤开展翻转课堂的教学实践：1)以课下网络学习或自学为辅，课堂讨论为主；2)课上讨论之前对小组成员集体指导，指导学生查找相关的学习资料以及需要讨论的重难点；3)课上讨论阶段对讨论小组得到的片面或错误的结论加以引导和修正；4)课后对未讨论清楚的问题进行答疑.对于翻转课堂的内容选取应遵循2个原则：1)理论性不宜太强，不宜包含过多定义以及过多定理的证明，学生通过自学和讨论可以理解；2)内容不宜过多，通过教师引导能在一次课的时间之内讨论完成.对于”高等数学“课程内容中2个重要极限、函数形态的研究、Hospital 法则、基于有理函数的积分、正项级数、一元以及多元函数的极值等内容均适合进行翻转课堂的教学.翻转课堂对于“高等数学”教学的意义在于：1)能调动和激发学生主动学习的兴趣与热情；2)能拉近师生之间的距离，改善传统课堂中师生之间互动不足的局面，让学生不仅仅是旁听者，也是参与者；3)让教师以学生角度和学生一起思考问题，有利于了解学生学习的程度和思考问题的角度，并适时调整教学计划.此外，对于传统课堂也要进行不断地改进，增加师生互动，让传统课堂和翻转课堂师生角色差别平稳过渡并逐渐缩小，最终让学生成为学习的主体，学生和老师均是学习的参与者而没有旁观者.

1.3 基于MOOCs的教学实践 自2011 年 12 月以来，美国陆续成立了由斯坦福大学、麻省理工学院等知名大学构建的 MOOCs 平台，如课程时代Coursera、在线大学 Udacity 和 EdX 等.2013 年北京大学、清华大学等高校率先宣布加入美国 MOOCs 三大主流机构之一的EdX，上海更是在全国率先成立了高校课程共享中心，且提供来自市内的 30 多所高校的学生进行选修平台上所提供的通识类课程并计入学分.

MOOCs创造了史无前例的网络大学课堂，大量的来自世界知名大学教授的视频课程被放到网上， MOOCs同时也关注学习者的需求与学习行为，应用各种日新月异的信息技术组织各种形式的互动、交流、评价和服务，由此推动着以教师讲授为中心的传统课堂向信息时代以学习者需求为导向的历史性转变，将以往封闭的传统大学课堂向全社会开放，开创了信息时代普及高等教育的新形式和新路径.但也有一些学者提出质疑，MOOCs 虽然提供免费的课程资源，但学生真正需要的却是教师提供的服务.学习者自主学习、信息搜索等能力的养成与批判性思维、探究精神等品质的形成都必须在传统课堂上通过与教师的互动达成并逐渐发展，而这些都是MOOCs 所不具备的[10].另外，目前对于MOOCs课程极高的弃课率和极低的保持率也反应了MOOCs课程在应用和普及方面有待完善，同时表明MOOCs课程的学习对学生的自觉性以及学习毅力具有很高的要求.

尽管MOOCs课程带来了一种全新的教学方式和理念，但是也存在着一些相比于传统课堂教学的不足，考虑到“高等数学”课程理论和系统性强的特点以及MOOCs课程较高的弃课率，对于“高等数学”课程大面积的使用MOOCs可能不太现实.另外，目前高校的教学改革对于基础课程的学习学时数进行了一定的压缩，开设的数学课程学时相对于学生要掌握的数学知识严重偏少，如何在课堂学时减少以及不降低教学效果情形下让学生有效的学到更多数学知识将是大学数学课程改革值得思考的一个问题.综上分析，可以进行MOOCs教学的探索和尝试：1)将每门课程的非核心部分的教学内容采用MOOCs教学.比如课程中带星号的章节，这部分内容在学时压缩情形下一般不会纳入教学学时，但这些内容为部分专业学生专业课学习的数学基础，比如“高等数学”课程中的多元函数的Taylor公式、向量值函数的导数、Fourier级数的复数形式、通量与散度以及环流量与旋度等.2)将课程内容的延伸内容作为MOOCs教学内容，拓宽学生知识的宽度和广度.比如对于“高等数学”的多元函数极值求解，可以让学生在学习完理论后通过MOOCs学习多元函数极值的数值求解方法并利用梯度下降法、遗传算法、蚁群算法等优化算法编程加以实现；对于微分方程的求解，在学习完微分方程求解理论后让学生进一步通过MOOCs课程学习微分方程的常见数值解法并利用编程加以实现.最后，教师应该为学生提供MOOCs课程的选择和参考，监督和评价学生的学习效果并对学生在MOOCs学习完成后仍然无法解决的问题进行答疑.

1.4 3种教学方法的综合运用以及融合 通过分析，3种教学方法适合针对不同学习内容来进行教学，在实际教学中可以根据教学内容不同特征采取研究性学习、翻转课堂、MOOCs以及传统教学方法中的一种或多种方法进行教学，学习内容的特征主要包括学习内容的理论深度和难易程度、知识点集中程度、知识点基础性程度，具体选择方案见图1所示.

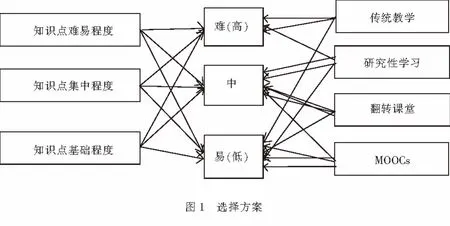
由图1可知，不同的学习方法可能适合2种程度的选择特征.对于知识点的难易程度，越高越适合采用排序偏上的方法；对于知识点的集中程度，越高越适合采用研究性学习方法；对于知识点的基础程度，基础程度高往往蕴含知识的必要性和重要性，适合采用传统教学方法，基础程度越低往往蕴含了知识的应用性、综合性，越适合采用翻转课堂以及MOOCs学习方法.因此，在实际教学中可以根据教学内容特征选择合适的教学方法，对于同一章或同一节中不同特征的知识点可以融合多种教学方法，达到取长补短，调动和激发大部分学生的积极性，引导学生积极有效的学习.

2 教学方法效果评价与分析

为了解多重教学方法与单一教学方法之间的差异，选取中国地质大学4个相近本科专业对“高等数学”课程实施3种教学方法，各抽取120份有效问卷进行分析，其中对4个相近本科专业中之一实施3重教学方法.问卷内容设置如表1所示，调查问卷满分100分，3种方法各对应表1中第一列的5个指标，合计15个指标，每一个指标通过其具体表现打分得到.得分分为4个档次，对每一项具体指标，完全实现为满分，大部分实现为满分的3/4，实现一部分为满分的1/2，实现很少为满分的1/4，完全没有实现为0分.对于3重教学方法，3种方法的得分权重按照学习内容多少的相对比例进行设置，研究性学习、翻转课堂以及MOOCs 3种教学方法权重分别取为0.4、0.4以及0.2.为方便显示调查指标分数，将120份问卷5个调查指标分数均接近的分为同一组，分为20组，平均每类问卷数为6份，图2为采用3种学习方法对应的20组问卷均值关于调查指标的分数均值分布图.由图2可知大部分问卷的指标的分数均值大于等于15分，说明3种方法实施效果均能取得比较满意的效果.

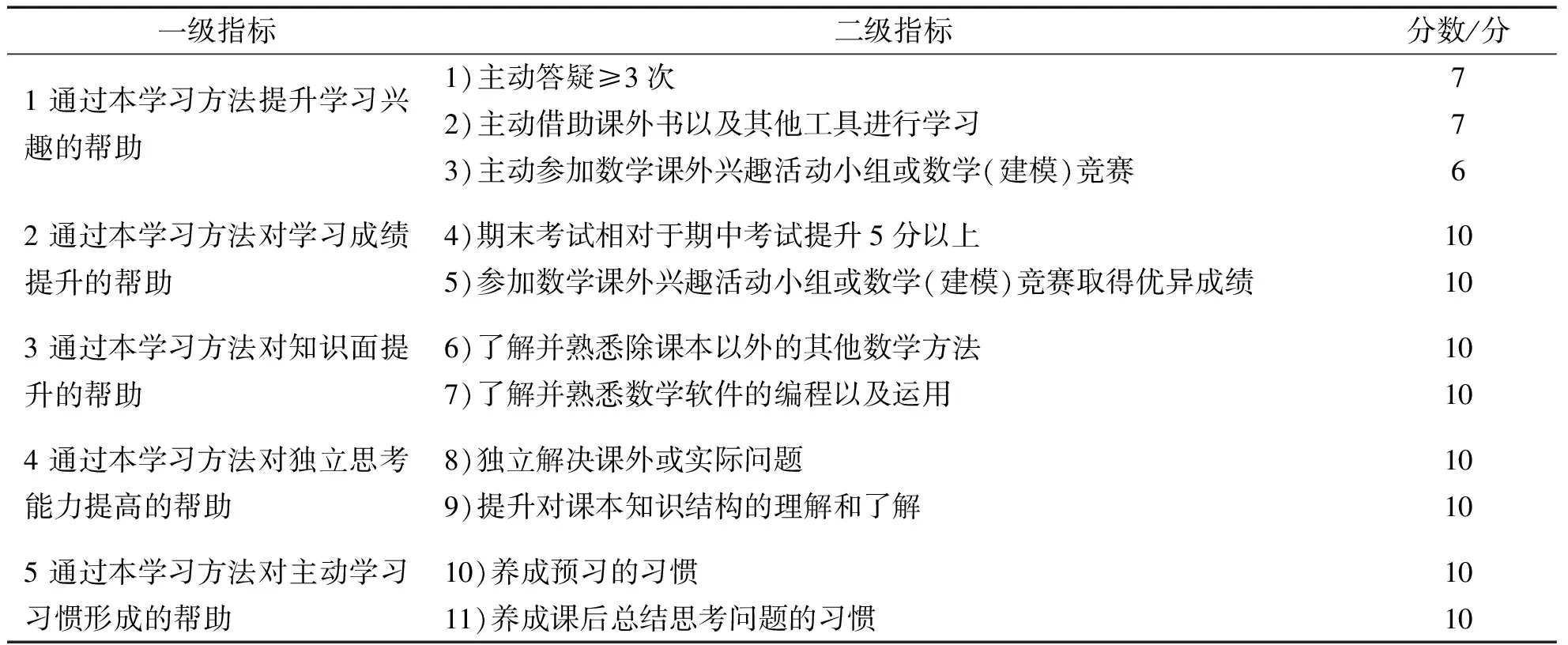
表1 3种教学方法学习效果调查问卷设置

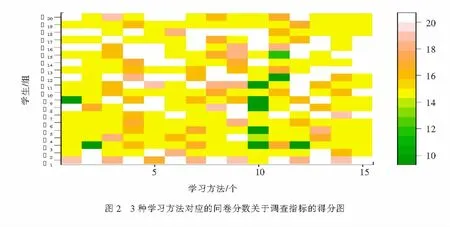
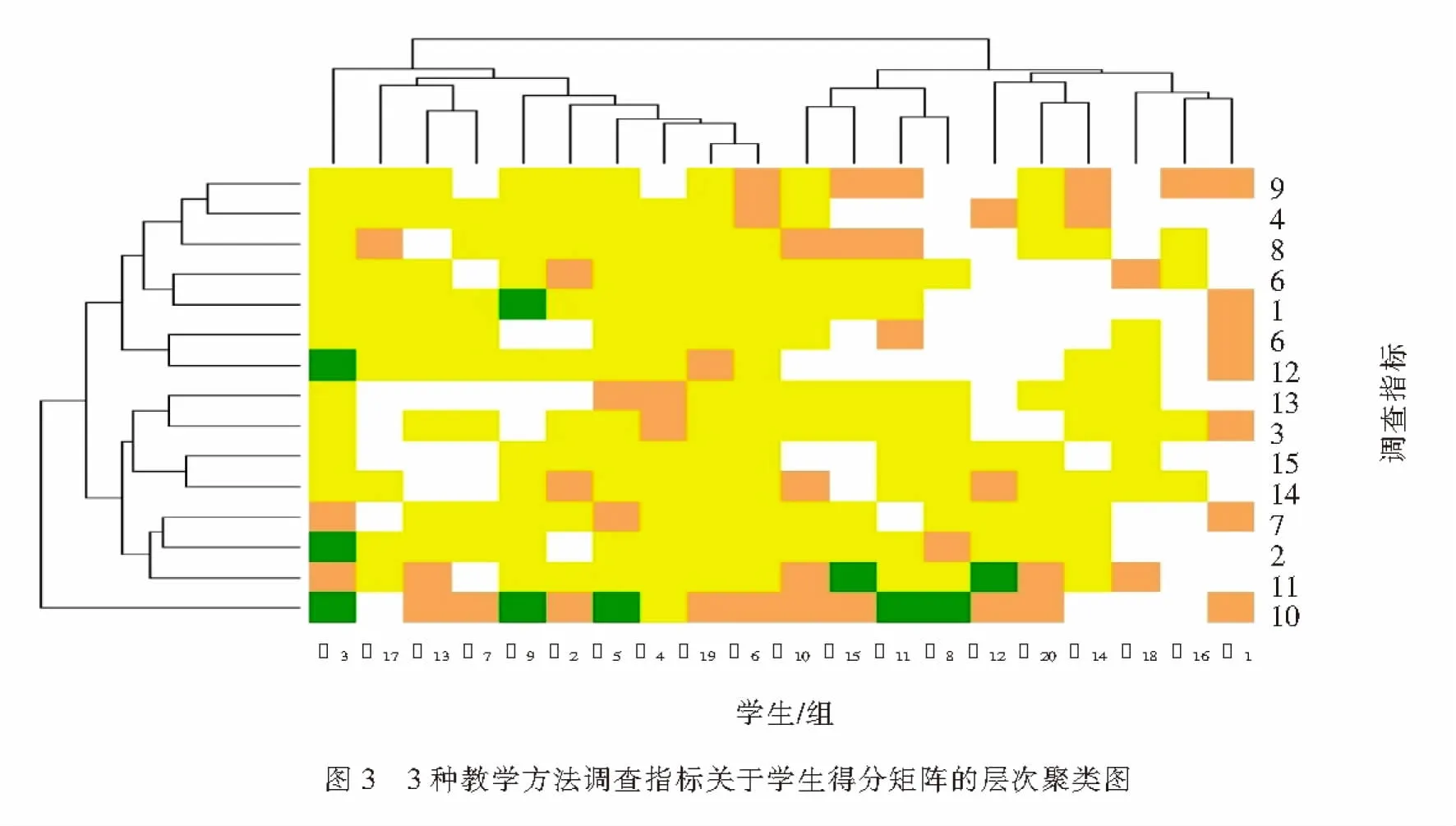
为了解3种教学方法以及各个指标之间的相关关系，对各个调查指标以及学生分组进行聚类，聚类距离计算选择欧几里得距离进行计算，方法选择基于完全链接的层次聚类方法.图3为3重教学方法调查指标关于学生得分矩阵的层次聚类图，为了了解指标之间的相关度，选取2～3个调查指标作为聚类小类，图3聚类结果显示共有如下小类：{4,8,9}, {1,6},{5,12}, {2,7,11},{14,15}, {3,13}.从聚类结果可见{4,9}，{1,6}，{2,7}，{3,13}对应不同学习方法的相同指标，将其归为一类说明各个学习方法在相同指标集中具备较高的相似认知.另外不同学习方法不同指标集也在同一类：{5,12}, {7,11}说明不同学习方法之间存在相互促进的关系和相似的影响.事实上，3种方法之间存在一定的相关关系，翻转课堂和MOOCs都需要学生利用课外网络或课本学习相应的知识点，研究性学习和翻转课堂均需要就某些问题展开师生讨论，3种方法均需要学生具备较好的主动学习状态.同一学习方法的不同指标也在同一类：{8,9}, {14,15}说明同一学习方法之间的不同指标存在相互影响和协同作用关系，{8,9}, {14,15}均说明独立思考能力和主动学习之间存在十分紧密的联系和相关关系.图4给出了调查的15个指标之间的相关性关系图，同类指标之间也存在较大的相关关系.最后，通过对学生的聚类分析也便于根据学生聚类特征将学生分成不同的类别进行教学以及管理.

图5为3重教学方法以及3种单一方法得到的问卷得分图，其中V1～V4分别对应3重教学方法、研究性学习、翻转课堂以及MOOC教学方法.从图5可知，对于大部分的调查问卷，3重教学方法的综合得分要高于其它单一的教学方法对应的问卷得分.

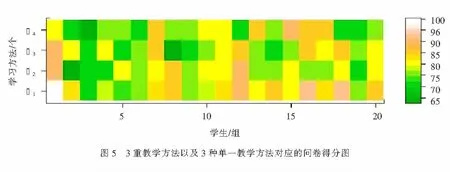
3 教学方法效果比较分析

为了了解图5中4种情形下的教学方法是否存在显著差异，利用W检验法、Bartlett检验、总体均值是否相等以及Scheffe检验法分别对4种情形下的总体分布、方差、总体均值以及两两均值进行假设检验.在总体均值存在显著差异基础上，进一步对两两总体均值差异利用样本方差分布进行了检验[11].

首先对4种情形下的均值是否相等进行显著性假设检验

H0:x1=x2=x3=x4，H1:x1，x2，x3，x4

至少有2个不等.检验步骤：

1)由于影响学习效果因素往往是多方面的，首先对4种情形下的总体分布是否为正态分布进行假设检验，采用W检验法进行检验，检验结果如表2所示.

表2 4种教学方法结果的W正态检验

由表2可知，4种情形下的W值均十分接近1，且所有P值均大于0.05，因此可以认为4种情形下的调查结果均服从正态分布.

2)对4种情形下的总体方差齐性进行假设检验

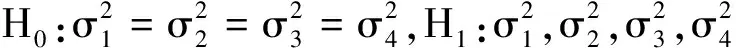
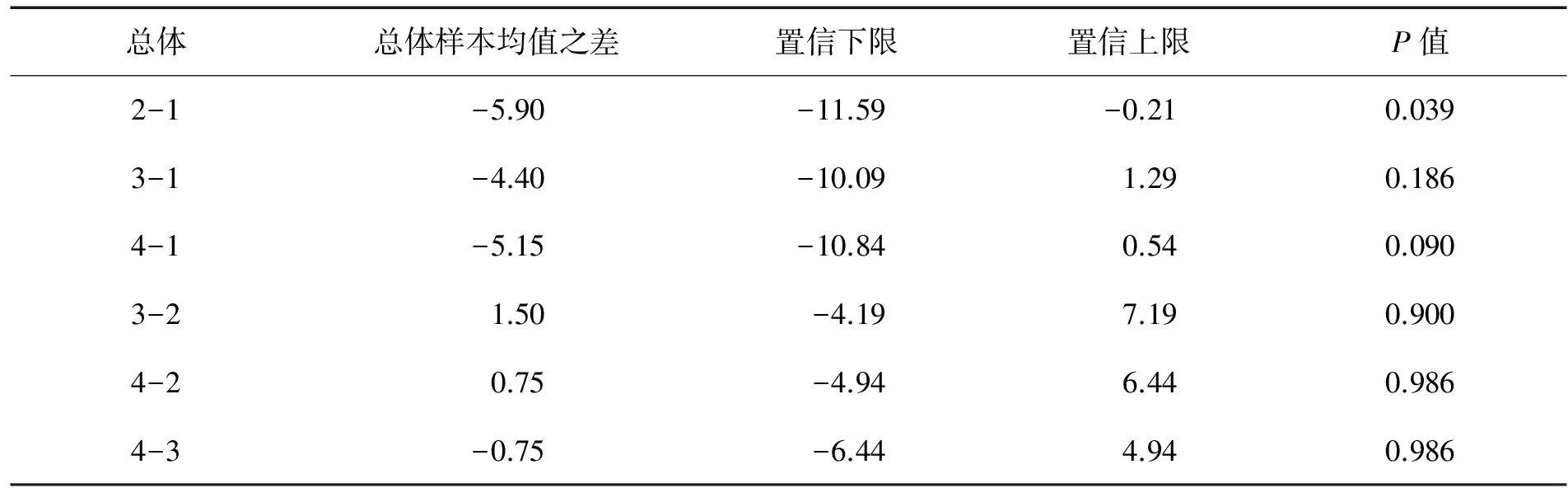
且Se与SA独立，因此

对于4个总体计算得到ST=3 982.9，Se=3 562.6，SA=420.3，F=2.989，取α=0.05，Fα(3,76)=2.725

其次，为了进一步了解3重教学方法以及单一教学方法教学之间差异，对4个总体均值进行两两比较

H0：xk=xl(k,l=1，2，…,r,k≠r)，H1：xk≠xl(k,l=1，2，…,r,k≠r).

根据Scheffe检验法，对于方差相同的正态总体有

根据以上分布以及4个总体样本均值之差得到4个总体两两之差的样本均值，95%置信区间如图6所示，置信区间上下限以及样本均值差及其P值见表3，其中1代表3重学习方法，2～4分别代表研究性学习，翻转课堂以及MOOCs.

表3 4个总体对应学习方法样本均值差异以及95%置信上下限和P值

总体总体样本均值之差置信下限置信上限P值2-1-5．90-11．59-0．210．0393-1-4．40-10．091．290．1864-1-5．15-10．840．540．0903-21．50-4．197．190．9004-20．75-4．946．440．9864-3-0．75-6．444．940．986

由图6可知，3重教学方法与3种单一方法总体均值相对于3种单一方法之间存在较为明显的差别.通过表3计算结果可得，4个总体对应学习方法中多重教学方法相对于其他3种单一教学方法，存在较大的样本均值差且其P值相对较小，而3种单一学习方法之间均值差异并不明显且均值差异P值较大.因此可以认为3重学习方法相对单一学习方法在总体均值上存在较大的提高.

4 小 结

首先从兴趣、成绩、知识面、独立思考能力以及学习习惯5个方面对研究性学习、翻转课堂以及MOOCs 单一以及综合教学方法实施效果进行了比较分析，3种单一以及综合教学方法在5个方面均有较高的得分；其次通过聚类分析分析了3种教学方法5个指标之间的相关关系，3种教学方法的不同以及相同指标之间均存在同类的情形，表明3种教学方法存在一定的相关关系以及协同关系，3种方法对学生学习的改善和促进方面存在一定的相似性，同一种方法对学生存在多方面的促进和影响；最后对3种方法综合运用的效果运用总体均值的统一比较以及两两比较的假设检验方法证实了3重教学方法的教学效果好于单一方法的教学效果，说明在实际教学中将3种教学方法加以灵活运用可以避免单一方法的不足，能够取得更好的教学效果.

[1] 郭戈. “研究性学习法”述评——苏霍姆林斯基的教学思想[J].教育理论与实践,1986,6(6):43-44.

[2] 何朝阳，欧玉芳，曹祁. 美国大学翻转课堂教学模式的启示[J]. 高等工程教育研究，2014(2):148-151，161．

[3] 宣葵葵. 美国大规模在线开放课程(MOOCs):特征、影响及争论[J]. 高教探索，2014(6):71-74．

[4]GannodGC,BurgeJE,HelmickMT.Usingtheinvertedclassroomtoteachsoftwareengineering:proceedingsofthe30thinternationalconferenceonsoftwareengineering,Leipzig,May10-18, 2008[C].[S.l.]:[s.n.],2008.

[5] 瞿振元．以MOOCs发展为契机促进信息技术与高等教育深度融合[J]．中国高等研究，2014(6):1-4．

[6] 陈国松. 我国重点大学本科工程教育实践教学改革研究[D]. 武汉：华中科技大学，2012．

[7] 中华人民共和国教育部.《国家中长期教育改革和发展规划纲要》(2010-2020年)[R].北京：中华人民共和国教育部,2010．

[8] 中华人民共和国教育部.《教育部关于实施“卓越工程师教育培养计划”的若干意见(征求意见稿)》[R].北京：中华人民共和国教育部,2010．

[9] 中华人民共和国教育部.《教育部等部门关于进一步加强高校实践育人工作的若干意见》[R].北京：中华人民共和国教育部,2012．

[10] 桑新民.MOOCs热潮中的冷思考[J]. 中国高教研究，2014(6):5-10．

[11]BickelPJ,DoksumKA.MathematicalStatistics,BasicIdeasandSelectedTopics[M].Portland:Taylor&Francis,2016.

Comparison and Analysis of Multiple Teaching Methods of Advanced Mathematics Course

Bian Jiawen, Yang Diwei, Fu Lihua, Li Hongwei

(School of Mathematics and Physics, China University of Geosciences, Wuhan 430074, China)

In the report, the course of advanced mathematics was used as an example, the comparison and analysis of the feasibilities of multiple teaching methods were performed, including inquiry learning, flipped class, and MOOCs. Based on interest, score, knowledge, independent thinking ability, and study habit, the implement effects were compared and analyzed.

math courses of universities; multiple teaching methods; research learning; inverted classroom; MOOCs

2017-01-04

中国地质大学(武汉)本科教学质量工程项目(ZL201634，ZL201739)，湖北省教学项目(2012142, 2012139)

边家文(1979-)，男，副教授，博士，博士后，研究方向：统计信号处理，E-mail:jwbian@cug.edu.cn

1004-1729(2017)02-0186-09

G 642

A DOl：10.15886/j.cnki.hdxbzkb.2017.0031