随机振动下产品包装件动态响应的实验研究和有限元分析

2017-07-18王志伟林深伟

振动与冲击 2017年13期

王志伟, 林深伟

(1. 暨南大学包装工程研究所，广东珠海 519070；2. 暨南大学产品包装与物流广东普通高校重点实验室，广东珠海 519070；3. 暨南大学珠海市产品包装与物流重点实验室，广东珠海 519070)

王志伟1,2,3, 林深伟1,2,3

实验研究了产品包装件在四种振动等级、三种约束方式下的随机振动特性，采用有限元法进一步分析固定约束方式下产品包装件的响应特性以及纸箱和衬垫的应力和变形情况。研究结果表明，产品的加速度响应功率谱主要取决于共振区域的激励加速度功率谱，包装起到了在共振区域的带通和放大作用。随着约束方式的加强，产品包装件共振频率增大，固定约束方式下的共振加速度功率谱峰值明显大于无约束和弹性约束方式下的共振加速度功率谱峰值。有限元计算得到的共振频率和产品加速度功率谱与实验结果较好吻合，产品加速度功率谱峰值对系统阻尼系数十分敏感。有限元法为物流随机振动环境作用下产品包装件的分析与设计提供了有效手段。

随机振动；产品包装；功率谱密度；约束方式；有限元分析

实际物流中，因路面不平而产生随机信号，来自运输工具的随机振动与冲击激励会对包装产品造成破损。所以，产品的包装防护设计应考虑随机振动与冲击的作用[1]。国内外学者对产品运输包装进行了广泛的研究，但大多集中在产品关键部件的冲击破损[2-5]和复杂运输包装系统振动的分析方法方面[6-7]。在包装产品随机振动的研究方面，运输过程振动信号调研及模拟方法的研究较多[8-10]，包装产品随机振动响应分析较少。秦璐等[11]采用ANSYS Workbench软件建立了路由器风扇组的有限元模型，进行了随机振动分析，验证了其包装设计的可行性。李晓刚[12]对车辆和包装产品构成的运输包装系统随机振动进行了频域分析，得到了产品及易损零件加速度响应的幅值频谱和功率谱密度。江春冬等[13]研究了随机振动下产品的破损机理，采用线性累积损伤理论对产品进行了振动疲劳计算。Wang等[14]采用压力感测片研究了三层堆码单元在不同随机振动路谱下纸箱接触面的动压、力穿越分布和产品的响应功率谱密度，为堆码包装设计提供了依据。

为防止包装产品在物流中的移动和相互碰撞，产品常常会通过约束固定其位置。随着物流快递行业的快速发展，对包装产品的约束捆绑形式变得多样化。不同的约束方式，对包装件振动特性会产生重要影响，而在这方面至今几乎没有研究。本文以水泥块(模拟产品)、乙烯-醋酸乙烯共聚物(Ethylene-Vinyl Acetate Copolymer, EVA)衬垫和4号邮政纸箱组成的产品包装件为研究对象，实验研究产品包装件在四种振动等级、三种约束方式下(无约束、弹性约束和固定约束)的随机振动特性。采用有限元法进一步分析固定约束方式下产品包装件的响应特性以及纸箱和衬垫的应力和变形情况，为缓冲包装设计提供依据。

1 材料和系统参数测定

实验和有限元分析用包装产品如图1所示，它由水泥块、EVA衬垫和瓦楞纸箱组成模拟产品包装件。瓦楞纸箱外尺寸为350 mm×190 mm×230 mm，水泥块质量17.5 kg，产品包装件质量18.0 kg。材料和系统参数测定如下。

(a)(b)

图1 产品包装件及加速度传感器固定位置

Fig.1 Package and position of acceleration sensor

(1) 纸箱瓦楞纸板弹性模量的测定。在纸箱瓦楞纸板上，沿垂直瓦楞方向切取10个160 mm×25 mm的矩形试样，沿瓦楞方向切取10个长为160 mm×40 mm并含五个完整瓦楞的矩形试样。将瓦楞纸板试样等效成均质梁，采用CMT2203微电子压力试验机，参考GB/T 9341“塑料-弯曲性能的测定”方法[15]，设置跨距为80 mm，以3 mm/min的加载速度对矩形试样进行三点弯曲试验，得到瓦楞纸板的载荷-挠度曲线，根据式(1)可计算瓦楞纸板试样的等效弹性模量E。

(1)

式中：L为试样跨距；b为试样宽度；δ为试样厚度；ΔP为载荷增量；ΔX为与ΔP对应的试样中点处的挠度增量。通过式(1)可计算得到瓦楞纸板垂直瓦楞方向的各试样等效弹性模量平均值为Ex=118.50 MPa，平行瓦楞方向的等效弹性模量平均值为Ey=64.30 MPa。瓦楞纸板厚度方向的弹性模量以及瓦楞纸板的剪切模量，根据文献给出的经验公式进行计算[16-17]，如式(2)所示。

(2)

式中：Ez为纸板厚度方向的弹性模量；G为剪切模量。瓦楞纸板的泊松比参照文献[18]给定。

(2) EVA衬垫弹性模量的测定。对EVA衬垫裁取10个70 mm×70 mm的方块试样，采用CMT2203微电子压力试验机，参照GB/T 8168“包装用缓冲材料静态压缩试验方法”进行测试[19]，获得EVA衬垫的压缩载荷-变形曲线。根据式(3)，可计算得到EVA衬垫试样的弹性模量。

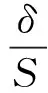
(3)

式中：δ为试样厚度；S为试样面积；ΔF为压缩试验的载荷增量；Δx为压缩试验的位移增量。通过式(3)可计算得到10组EVA衬垫弹性模量平均值为EEVA=1.20 MPa。

在有限元分析中，需用到水泥块(模拟产品)、木板(用于固定产品包装件)和振动台的材料参数。相对于包装材料而言，这些参数都很大，在有限元计算中取大值进行计算。相关参数见表1。

表1 材料的相关参数

(3) 系统阻尼比的测定。将图1所示产品包装件采用木板和螺栓组成的固定装置将其固定在振动台上，加速度传感器固定在水泥块顶端，如图2(c)所示。进行加速度为0.365 g和0.516 g的两组扫频试验，扫频范围3～100 Hz，扫频速度10 Hz/min，得到水泥块的传递率曲线。利用半功率带宽法式(4)，计算得到包装系统阻尼比的范围为0.06～0.07，水泥块的平均共振频率为54.49 Hz。

(4)

2 随机振动试验

2.1 试验方法

采用美国Lansmont公司振动测试系统(Model 7000-10)对产品包装件进行随机振动试验。将其置于振动台中心位置，分三种约束方式进行随机振动。一是无约束方式，二是弹性约束方式，三是固定约束方式。无约束方式是将包装件直接放置在振动台上，见图2(a)；弹性约束方式是利用弹性绳对包装件进行绑定，见图2(b)。弹性绳刚度为1.29 N/mm，对产品包装件产生的压力为41.6 N；固定约束方式则是采用固定装置将包装件固定在振动台上，限制包装件上下跳动，见图2(c)。

采用美国ASTM D-4169标准中加速度谱[20]和自行设定的非标准加速度谱Level IV进行随机振动试验，各试验的加速度功率谱(Power Spectrum Density，PSD)描述见表2。振动台的采样时间为5 min，振动台的输入信号将作为有限元分析时的输入激励，水泥块的加速度响应将与有限元计算的结果进行比较。

(a) 无约束方式

(b) 弹性约束方式

表2 随机振动加速度功率谱

2.2 结果分析

通过随机振动试验，得到不同振动等级、不同约束方式下水泥块的加速度响应功率谱，如图3所示。由于120～200 Hz，实验得到的水泥块加速度功率谱越来越接近于0，故只截取3～120 Hz的结果。试验时采用了三个平行的产品包装件试样，分别以1#、2#和3#表示。

从图3可看出，同一振动等级下，随着约束方式的加强，水泥块的共振频率增大；尽管振动激励能量主要在4～20 Hz区域，在共振区域很小，但水泥块响应振动能量却主要集中在共振区域。水泥块的加速度响应PSD主要取决于共振区域的激励加速度PSD，包装起到了在共振区域的带通和放大作用；无约束方式和弹性约束方式的共振PSD峰值比较接近，固定约束方式的共振PSD峰值明显大于前两者，约束方式对共振PSD峰值有一定影响。同一约束方式下，随着振动等级(加速度均方根值Grms)由0.731 g降到0.516 g、0.365 g和0.258 g时，水泥块PSD明显下降，其共振频率略有增大。图3也表明，三个平行产品包装件试样的数据有较大分散性，水泥块在随机振动试验中有跳动现象发生。

(a) 无约束方式

(b) 弹性约束方式

(d) 无约束方式

(e) 弹性约束方式

(f) 固定约束方式

(g) 无约束方式

(h) 弹性约束方式

(i) 固定约束方式

(j) 无约束方式

(k) 弹性约束方式

(l) 固定约束方式

3 随机振动有限元分析

3.1 有限元模型建立

为相互验证，同时也为了发展物流随机振动环境作用下产品包装件的有效分析与设计技术，本文采用有限元技术分析了上述产品包装件在固定约束方式下的随机振动响应。

根据包装件的实际和固定约束方式，在Solidworks软件中建立三维实体模型，将其导入到Ansys Workbench软件的模态分析和随机振动模块中，进行随机振动分析。

材料属性设定。根据表1中的材料参数设定材料属性。

接触类型设定。考虑包装件在振动过程中各部件的实际接触情况，定义水泥块与前后左右EVA衬垫为不分离接触，与上下EVA衬垫为无摩擦接触；前后左右EVA衬垫与纸箱为不分离接触，上下EVA衬垫与纸箱为绑定接触；纸箱与振动台和木板实体为绑定接触。

单元与网格划分。瓦楞纸板设置为壳单元(Shell 181)，螺栓等效成弹性单元，刚度取大值为1.0×1010N/mm，其它均设为实体单元(Solid 186)。产品包装件网格划分如图4所示，单元数为9 234个，节点数为44 788个。

在振动台竖直方向上输入加速度功率谱，系统阻尼系数设置为0.07。

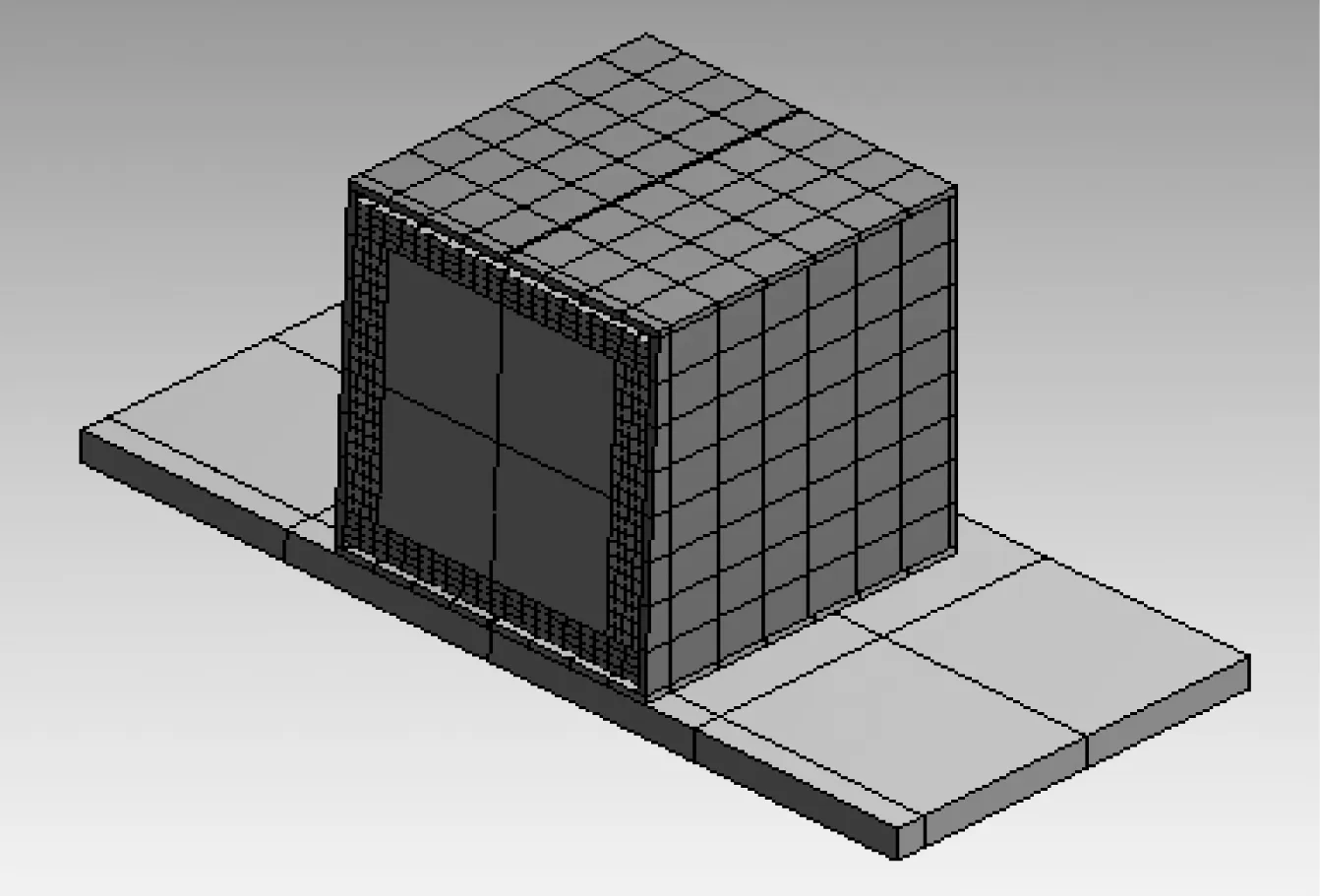
(a) 包装件剖面

(b) 固定约束方式模型

3.2 结果分析

有限元得到的水泥块竖直方向上的加速度功率谱画在图3(c)、图3(f)、图3(i)和图3(l)中。有限元计算得到的共振频率为56.405 Hz，与实验结果较好吻合。有限元得到的水泥块加速度PSD趋势与实验结果一致，能够较好地反映产品包装件的振动特性。由于实验中存在几何和接触等非线性，有限元分析还存在一定误差。需要指出的是：有限元得到的水泥块加速度PSD峰值与实验结果符合不很好，可能是由于在有限元分析中系统阻尼系数统一设置为0.07所引起。有限元分析发现水泥块加速度PSD峰值对系统阻尼系数十分敏感，而产品包装件系统阻尼系数随激励振动等级的变化而变化，且有较大的分散性。

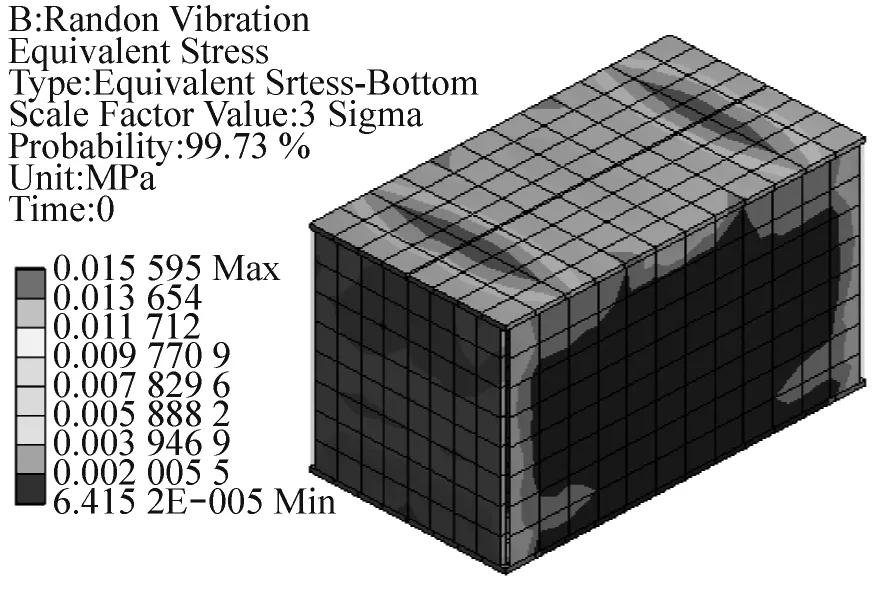
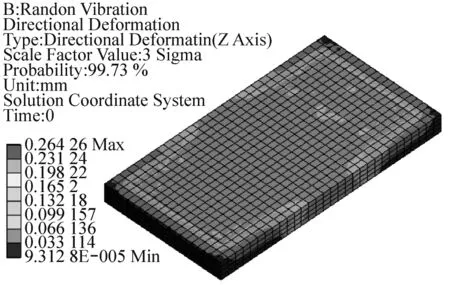
纸箱的竖直方向上的3σ变形云图和3σ等效应力云图表示在图5和图6中。振动水平从较高等级(Level I)变化到较低等级(Level IV)，相应的纸箱最大变形量不超过0.317 mm、0.224 mm、0.158 mm和0.112 mm的概率为99.73%，纸箱最大等效应力不超过0.044 MPa、0.031 MPa、0.022 MPa和0.016 MPa的概率为99.73%。对固定约束方式的纸箱，变形主要发生在长襟片与木板接触的区域。

(a) Level I

(b) Level II

(d) Level IV

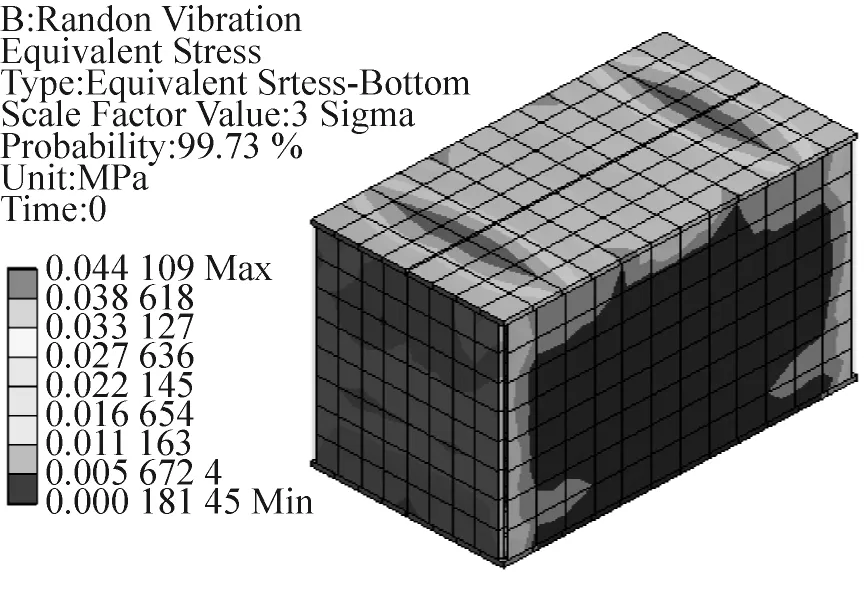
底层EVA衬垫的竖直方向上的3σ变形云图和3σ等效应力分布云图分别如图7和图8所示。振动水平从较高等级(Level I)变化到较低等级(Level IV)，相应的底层EVA衬垫发生最大变形量不超过0.374 mm、0.264 mm、0.187 mm和0.132 mm的概率为99.73%，最大等效应力不超过0.034 MPa、0.024 MPa、0.017 MPa和0.012 MPa的概率为99.73%。变形分布在衬垫与水泥块接触的区域，应力主要分布在衬垫与水泥块接触的两端区域，最大变形和最大等效应力发生在衬垫与水泥块边缘接触的位置。

(a) Level I

(b) Level II

(d) Level IV

(a) Level I

(b) Level II

(d) Level IV

(a) Level I

(b) Level II

(d) Level IV

对底层EVA衬垫的最大等效应力点进行应力响应功率谱分析，如图9所示。随着振动等级的增加，等效应力功率谱明显增大，共振区域应力功率谱变得十分陡峭。由于衬垫的应力与水泥块的加速度相关，图9中底层EVA衬垫最大等效应力功率谱与图3中水泥块的加速度功率谱形状一致。

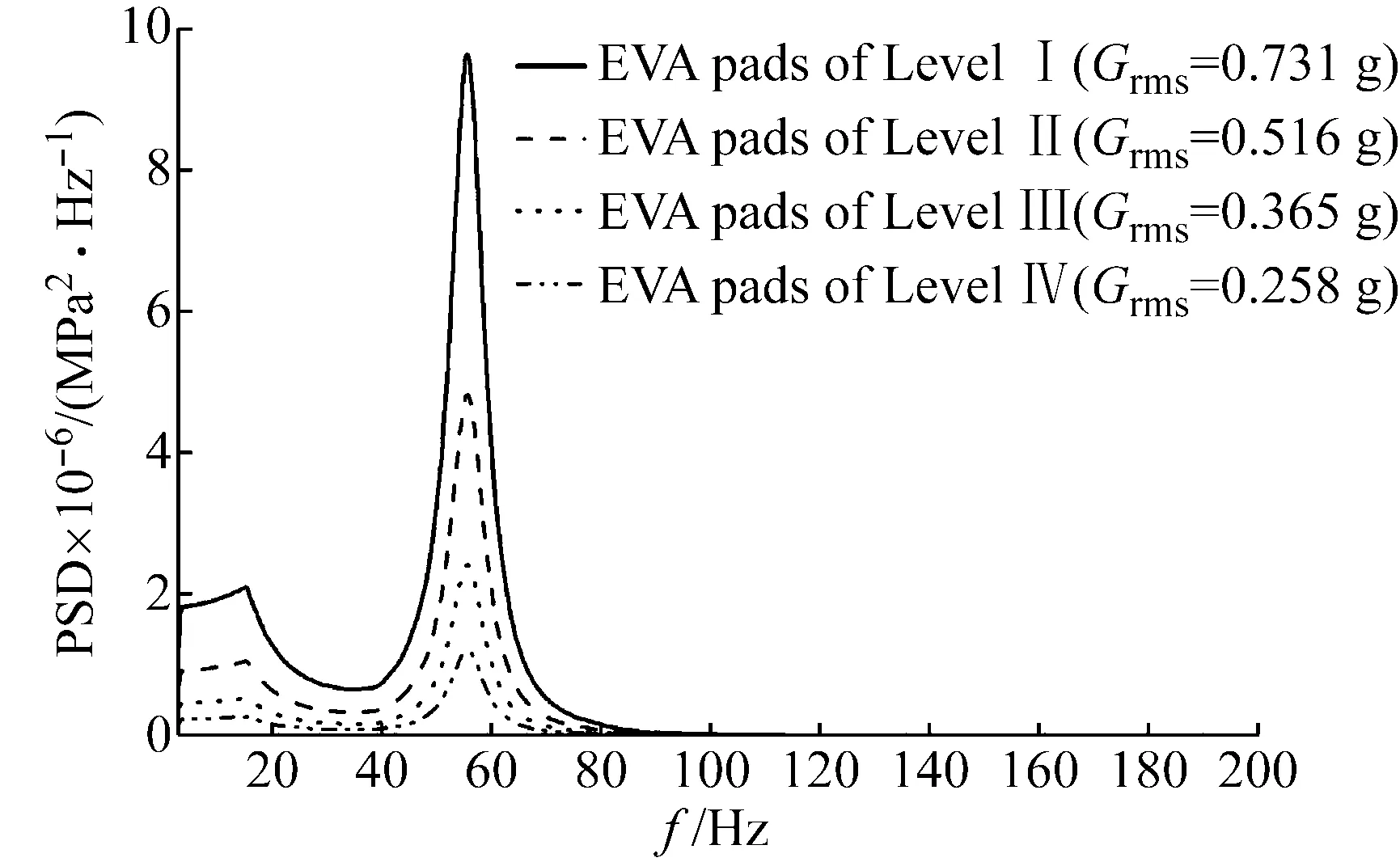
图9 底层EVA衬垫最大等效应力功率谱

4 结论

本文实验研究不同随机振动等级、不同约束方式下的产品包装件加速度振动特性，采用有限元法进一步分析固定约束方式下产品包装件的响应特性以及纸箱和衬垫的应力和变形情况。主要得出以下结论：

(1) 水泥块的加速度响应PSD主要取决于共振区域的激励加速度PSD，包装起到了在共振区域的带通和放大作用。同一振动等级下，随着约束方式的加强，水泥块的共振频率增大。固定约束方式的共振加速度PSD峰值明显大于无约束方式和弹性约束方式下的共振加速度PSD峰值，约束方式对共振PSD峰值有一定影响。同一约束方式下，随着振动等级的下降，水泥块加速度PSD明显下降，其共振频率略有增大。

(2) 产品包装件实际试样的随机振动响应数据有较大分散性，随机振动过程中产品在包装箱内会有跳动现象发生。

(3) 有限元计算得到的共振频率和产品加速度PSD曲线趋势与实验结果较好吻合，表明有限元法可为物流中产品包装件的分析与设计提供有效手段。同时，有限元分析还可得到产品包装任一点的等效应力响应PSD以及在一定概率下的变形云图和等效应力云图。有限元分析发现产品加速度PSD峰值对系统阻尼系数十分敏感。

(4) 物流中产品包装设计应重点控制系统共振区域和考虑产品包装件的约束方式。

[1] 王志伟. 现代包装力学[J]. 包装工程, 2002, 23(1): 1-5.

WANG Zhiwei. Modern packaging mechanics[J]. Packaging Engineering, 2002, 23(1): 1-5.

[2] 陈安军. 非线性包装系统跌落冲击问题变分迭代法[J]. 振动与冲击, 2013, 32(18): 105-107.

CHEN Anjun. Variational iteration method for dropping shock problem of a cubic non-linear packaging system[J]. Journal of Vibration and Shock, 2013, 32(18): 105-107.

[3] WANG Z W, JIANG J H. Evaluation of product dropping damage based on key component[J]. Packaging Technology and Science, 2010, 23(4): 227-238.

[4] 卢富德, 陶伟明, 高德. 具有简支梁式易损部件的产品包装系统跌落冲击研究[J]. 振动与冲击, 2012, 31(15): 79-81.

LU Fude, TAO Weiming, GAO De. Drop impact analysis on item packaging system with beam type elastic critical component[J]. Journal of Vibration and Shock, 2012, 31(15): 79-81.

[5] 计宏伟, 王心宇, 王佼, 等. 硒鼓缓冲气柱包装冲击响应与变形行为的图像测量分析[J]. 振动与冲击, 2012, 31(19): 151-155.

JI Hongwei, WANG Xinyu, WANG Jiao, et al. Shock response and deformation behavior analysis for a toner air-cushion package with drop impact tests and high-speed digital photography[J]. Journal of Vibration and Shock, 2012, 31(19): 151-155.

[6] WANG Z W, WANG J. Inverse substructure method of three-substructures coupled system and its application in product-transport-system[J]. Journal of Vibration and Control, 2011, 17(6): 943-951.

[7] WANG Z W, ZHANG Y B. Dynamic characteristic analysis of refrigerator-truck transport system by using inverse substructure method[J]. Packaging Technology and Science, 2014, 27(11): 883-900.

[8] LEPINE J, ROUILLARD V, SEK M. Review paper on road vehicle vibration simulation for packaging testing purposes[J]. Packaging Technology and Science, 2015, 28(8): 672-682.

[9] SINGH S P, SINGH J, SAHA K. Measurement and analysis of physical and climatic distribution environment for air package shipment[J]. Packaging Technology and Science, 2015, 28(8): 719-731.

[10] 朱大鹏, 李明月. 铁路非高斯随机振动的数字模拟与产品包装响应分析[J]. 包装工程, 2016, 37(1): 1-4.

ZHU Dapeng, LI Mingyue. Digital simulation of non-Gaussian random vibration of railway and packaging system response analysis[J]. Packaging Engineering, 2016, 37(1): 1-4.

[11] 秦璐, 丁毅, 苏杰. 基于ANSYS Workbench的路由器风扇组包装的包装动力学应用研究[J]. 包装工程, 2013, 34(13): 56-58.

QIN Lu, DING Yi, SU Jie. Applied research of packaging dynamics of router fan assembly packaging based on ANSYS Workbench[J]. Packaging Engineering, 2013, 34(13): 56-58.

[12] 李晓刚. 运输包装系统随机振动频域分析[J]. 包装工程, 2012, 33(15): 50-54.

LI Xiaogang. Random vibration frequency domain analysis of transport packaging system[J]. Packaging Engineering, 2012, 33(15): 50-54.

[13] 江春冬, 武玉维, 杜太行, 等. 包装件在随机振动下的破损机理及相关量检测[J]. 中国测试, 2015, 41(8): 27-30.

JIANG Chundong, WU Yuwei, DU Taihang, et al. Damage mechanism of the package under random vibration and the detection of relevant quantities[J]. China Mesurement & Test, 2015, 41(8): 27-30.

[14] WANG Z W, FANG K. Dynamic performance of stacked packaging units[J]. Packaging Technology and Science, 2016, 29(10): 491-511.

[15] 塑料-弯曲性能的测定：GB/T 9341—2008[S]. 北京: 中国标准出版社, 2008.

[16] MANN R W, BAUM G A, HABEGER C C. Determination of all nine orthotropic elastic constants for machine-made paper[J]. Tappi, 1980, 63(2): 163-166.

[17] BAUM G A, BRENNAN D C, HABEGER C C. Orthotropic elastic constants of paper[J]. Tappi, 1981, 64(8): 97-101.

[18] NORDSTRAND T M. Parametric study of the post-buckling strength of structural core sandwich panels[J]. Composite Structures, 1995, 30(4): 441-451.

[19] 包装用缓冲材料静态压缩试验方法：GB/T 8168—2008[S]. 北京：中国标准出版社, 2008.

[20] Practice for performance testing of shipping containers and systems: ASTM D-4169-14[S]. USA: ASTM International, 2014.

Tests and FE analysis for dynamic responses of packaged products under random vibration environment

WANG Zhiwei1,2,3， LIN Shenwei1,2,3

(1. Packaging Engineering Institute, Jinan University, Zhuhai 519070, China; 2. Key Laboratory of Product Packaging and Logistics of Guangdong Higher Education Institutes, Jinan University, Zhuhai 519070, China; 3. Zhuhai Key Laboratory of Product Packaging and Logistics, Jinan University, Zhuhai 519070, China)

The random vibration characteristics of packaged products under four vibration levels and three constraint modes were investigated. The FE method was applied to analyze response features of product packages with fixed constraint, and stresses and strains of carton box and pad. The results indicated that the response acceleration power spectral density (PSD) of products depends mainly on the excitation acceleration PSD in resonance area; the packaging has performances of bandpass and amplification; the resonance frequency of packaged products increases with enhancement of constraints; the peak of the resonance acceleration PSD of products under a fixed constraint is obviously bigger than those of products under unrestraint and an elastic constraint, respectively; resonance frequencies and acceleration PSDs of products obtained with the FE method agree well with those of tests; the peak of acceleration PSDs of products is sensitive to the damping coefficient of the system; the FE method provides an effective means for analysis and design of product packaging under random vibration environment.

random vibration; product packaging; power spectral density; constraint condition; finite element (FE) analysis

国家自然科学基金(50775100)

2016-04-06 修改稿收到日期：2016-05-23

王志伟男，博士，教授，博士生导师，1963年生 E-mail：wangzw@jnu.edu.cn

TB48；TH113.1

10.13465/j.cnki.jvs.2017.13.035