盾构隧道橡胶止水衬垫防水性能研究

□文/史 鹏 段景川

目前，盾构隧道接缝防水主要采用密封衬垫，分为弹性橡胶密封垫和遇水膨胀橡胶密封垫，遇水膨胀橡胶一般用在双道止水系统中，主要的防水能力仍然取决于弹性密封衬垫[1]。关于弹性密封衬垫力学性能和防水机制的研究主要集中在数值分析和试验研究两个方面。

试验研究方面，拓勇飞等[2]对不同断面的弹性橡胶密封垫进行高水压防水能力试验以及密封衬垫装配力试验，综合分析试验结果确定最优防水设计方案；陆明[3]以上海外滩隧道工程为例，对遇水膨胀橡胶挡水条、聚氨酯弹性体挡水条、三元乙丙弹性橡胶密封垫的短期和长期防水性能进行试验研究，得到了密封构件在正常状态和老化状态下的防水性能；钟小春等[4]针对三元乙丙橡胶防水衬垫，实施了恒定压缩永久变形和老化长期防水性能试验研究，结果表明：橡胶的老化系数在0.9 以上，恒定永久压缩应变＜15.4%，具有良好的长期防水性能。数值分析方面，雷振宇[5]通过对压缩变形情况下弹性橡胶密封衬垫的孔洞合理变形、薄弱处应力集中、完全压缩到沟槽时压力大小、最大张开量下接触应力的大小及分布等多因素的综合分析，提出以密衬垫表面接触应力和完全压缩到沟槽内的闭合压力作为盾构隧道管片接头弹性橡胶密封衬垫断面设计的指标；欧阳文彪[6]采用显式有限元法对密封衬垫压缩过程进行三维模拟并将分析结果与力学试验对比，同时对影响密封衬垫力学性能的多种因素进行分析，结果表明：有限元计算结果与试验结果具有一致性；橡胶硬度越大，开孔率越低，则橡胶密封衬垫越硬，越难压缩。

以上试验方法成本较高、费时并且难以获得密封衬垫内力和接触面接触应力的分布情况。现有数值模拟方法多集中于密封衬垫本身的压缩性能，对渗水路径接触应力没有进行区分研究，研究成果也难以推广用于衬砌结构受力分析。本文采用数值模拟的方式，对密封衬垫在不同压缩量和错开量的情况下，不同渗水路径的接触应力进行研究并获得密封衬垫压缩量与压缩合力的拟合关系式。

1 工程概况

天津地铁10 号线财经大学—微山路站盾构法隧道外径6.2 m、内径5.5 m，错缝拼装，采用C50钢筋混凝土管片，管片幅宽1.5 m，抗渗等级≥P10，区间最大水压0.2 MPa。管片接缝采用外侧双道防水，靠外侧为遇水膨胀橡胶密封垫，靠内侧为三元乙丙橡胶密封垫。考虑隧道在设计年限内，密封衬垫会出现应力松弛和老化现象并且管片的拼装误差会造成隧道接缝的张开和错缝，因此弹性橡胶密封垫防水压力设计值通常会在承受最大水压力值的基础上乘以一个安全系数。根据DBJ 08-50—1996《盾构法隧道防水技术规程》规定：设计水压应为实际承受最大水压的2～3 倍。本工程中安全系数取2，以0.40 MPa 的防水压力作为控制值。

设计弹性橡胶密封衬垫断面见图1。橡胶硬度为50 HA，将两个密封衬垫压缩至设计高度共需要压缩1.6 cm，每个密封衬垫压缩0.8 cm。

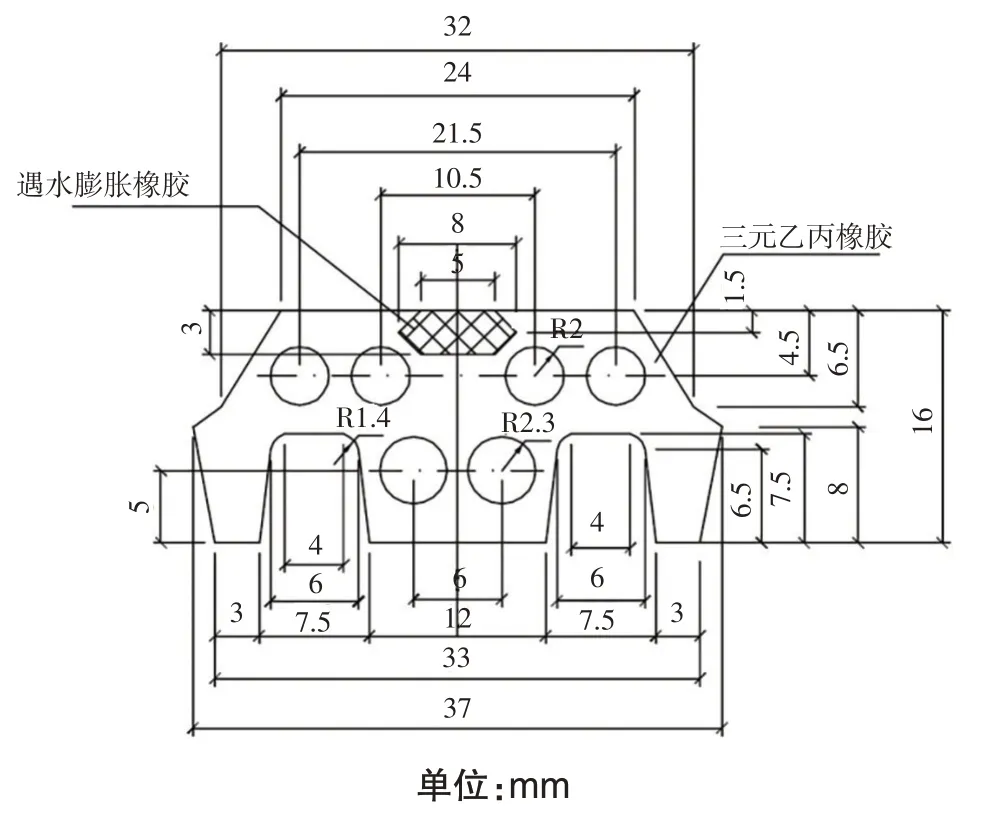
图1 密封衬垫结构断面

2 有限元数值模型

弹性橡胶密封垫断面和纵向尺寸相差悬殊，因此建立基于平面应变的混凝土-密封衬垫简化模型，见图2。

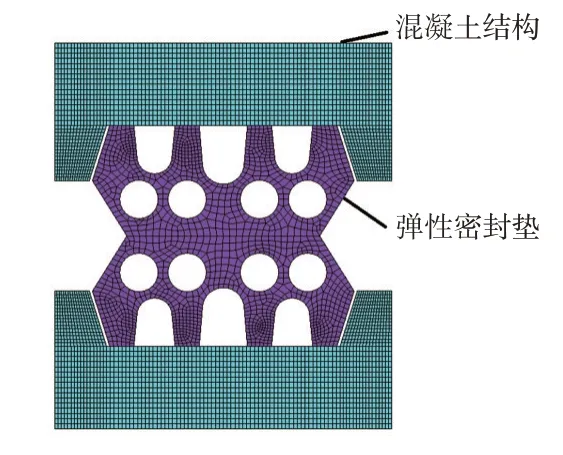
图2 衬垫与混凝土模型

C50 混凝土采用弹性本构模型，弹性模量取34.5 GPa，泊松比取0.167。橡胶材料通常被处理为各向同性不可压缩超弹性材料，应力-应变关系主要通过应变能函数来定义。在应变能密度函数模型中，Mooney-Rivlin模型是比较经典的，可以模拟橡胶材料的力学行为[7],其应变能表达式为

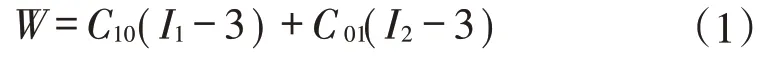
式中：W为应变势能；I1、I2为应变不变量；C10、C01为材料参数，通过试验取得，本模型C10取0.289 7，C01取0.059 9。

2.1 接触设置

在接触分析中，两物体A 和B 接触的一般情况见图3。

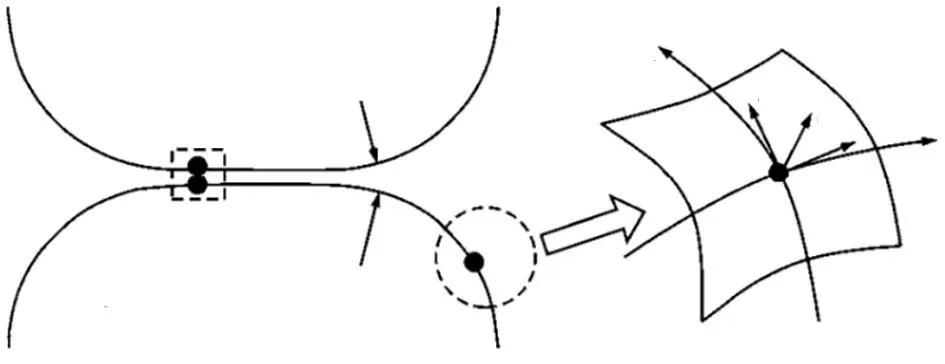
图3 物体间相互接触

图3 中，tVA和tVB表示两物体t时刻的位置，tSA和tSB表示两个物体可能发生接触的表面。

假设tSA上一点P与tSB发生接触，将点P在tSB上的投影点记为Q，则P-Q组成了接触分析的最基本单元，即接触点对。将点P和Q分别称为从接触点和主接触点，将面tSA和面tSB分别称为从接触面和主接触面。接触分析可在多套坐标系下进行，在接触面tSB上一点G附近，tSB可以解析化为参数曲面tSB(ξ,η)。

基于tSB的外法向还可以建立局部正交坐标系其中是点G在面tSB上的外法向，记为分别记为曲面参数坐标系适用于度量从点在主面上的累积滑移量，局部正交坐标系则适用于分解接触力、相对速度等物理量。

2.2 接触边界条件

1）不可贯入条件，即运动过程中独立的固体间不会发生相互贯穿，可表示为

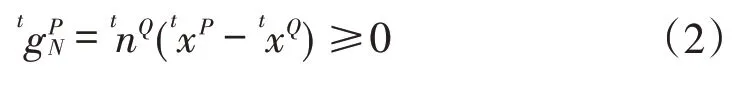
2）法向压力条件，是指在不考虑界面粘结作用的情况下，接触面之间的法向应力不能为拉应力。

3）摩擦力条件，是指接触点对间的切向相互作用力决定于法向压力和相对运动模式。基于工程上普遍采用的库伦摩擦定律来描述，式（3）对应静摩擦即粘结状态，式（4）对应滑动摩擦即滑移状态

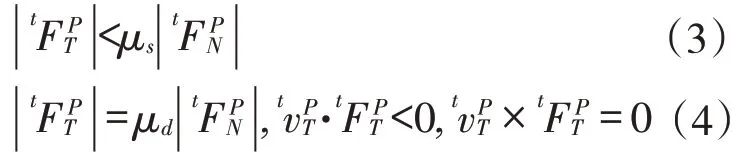
式中：μs和μd分别为静摩擦因数和动摩擦因数，工程应用中常近似认为μs=μd，以简化问题的描述和计算为从点沿切平面的相对速度。

在t+t时刻，考虑A、B 两物体发生接触的虚功原理可以表示为

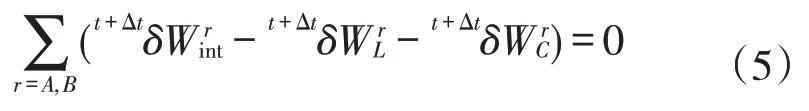
式中：δWint、δWL和δWC分别为内能、外荷载虚功和接触力虚功的变分。

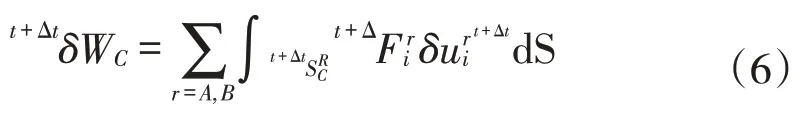
式中：tF为接触力分布；δu为质点位移的变分。

采用ANSYS 中的contac171 和target169 二维接触单元模拟密封衬垫与混凝土槽以及密封衬垫自身的接触作用，contac171为从面接触单元，target169为主面接触单元，其中，混凝土槽与密封衬垫的接触采用标准接触（standard）形式，即接触面可以闭合、张开，接触面滑移时产生摩擦力。混凝土与密封衬垫的静摩擦系数取0.5；密封衬垫的自接触同样采用标准接触形式，密封衬垫自接触静摩擦系数取0.8。下方管片下边界施加全方向约束；上方管片仅对上表面节点进行竖向的节点耦合约束，防止其产生旋转。

2.3 分析工况

由于盾构管片的拼装误差以及拼装完成后周围土体受到扰动导致的衬砌环变形，管片接头会张开或者错缝，影响密封垫的止水性能。分别对密封衬垫错开0、0.5、1、1.5、2 cm共5种工况进行压缩力学性能计算。

2.4 渗水路径

密封衬垫接触应力决定了密封衬垫的防水性能，水可以由3 个路径通过密封衬垫，即上侧密封衬垫与混凝土管片的接触面、上下密封衬垫接触面、下侧密封衬垫与混凝土管片接触面，见图4。

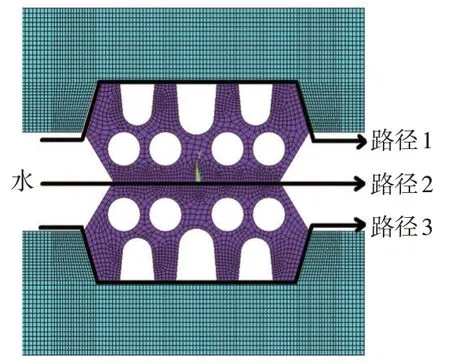
图4 渗水路径

实际情况中，水通过的路径为沿途接触应力峰值最小的路径。密封衬垫可以承受的水压力为实际路径沿途接触应力的峰值，一旦水压力大于实际路径沿途接触应力峰值，则认为橡胶密封衬垫的防水性能失效。

3 结果分析

3.1 密封衬垫变形

以工况1 计算结果为例，最终压缩量为1.6 cm，见图5。

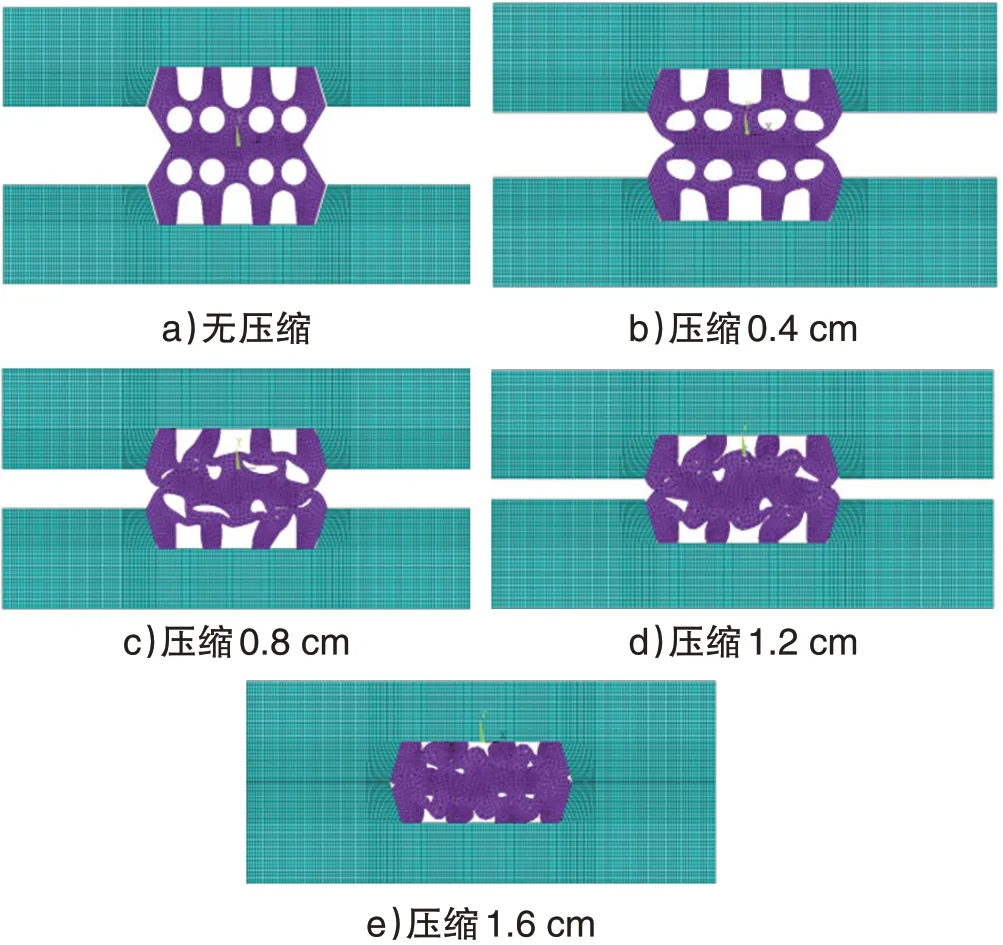
图5 工况1衬垫不同压缩量的变形

密封衬垫在压缩过程中产生了较大变形，其中心圆孔被挤压闭合，支撑脚变粗，两侧支撑脚与管片密封衬垫槽侧壁由分离变为紧密贴合，压缩完成后，密封衬垫较好的填充了管片的密封衬垫槽。图6为工况2～5完全压缩状态下的密封衬垫变形情况。

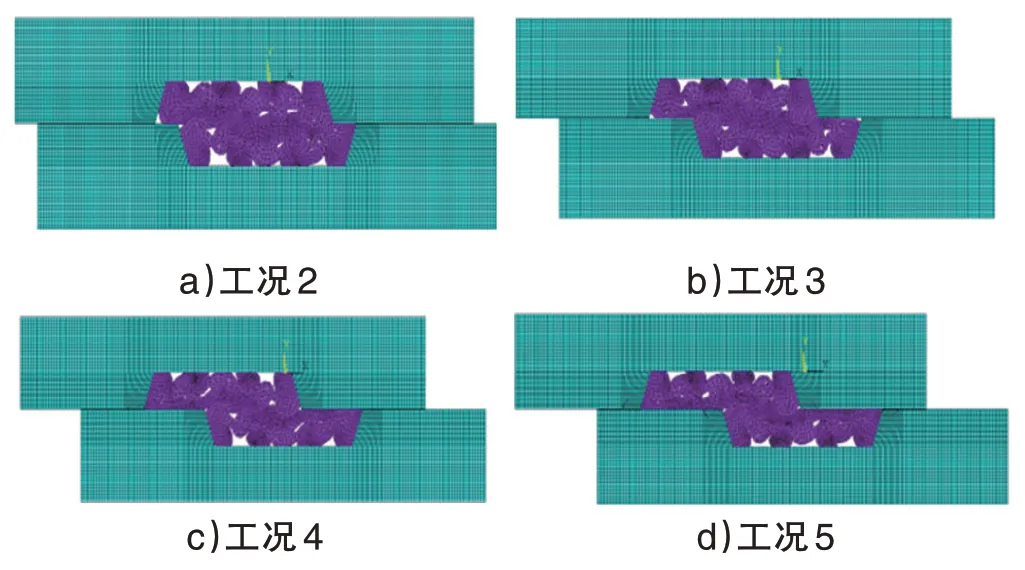
图6 工况2～5衬垫压缩1.6 cm变形

由图6 可以看出，工况2～5 中密封衬垫的变形与工况1 类似，在压缩1.6 cm 时密封垫都可以较好填充管片密封衬垫槽的空间。

3.2 密封衬垫内力

工况1 中不同压缩量下胶密封衬垫的Von-Mises应力分布见图7。

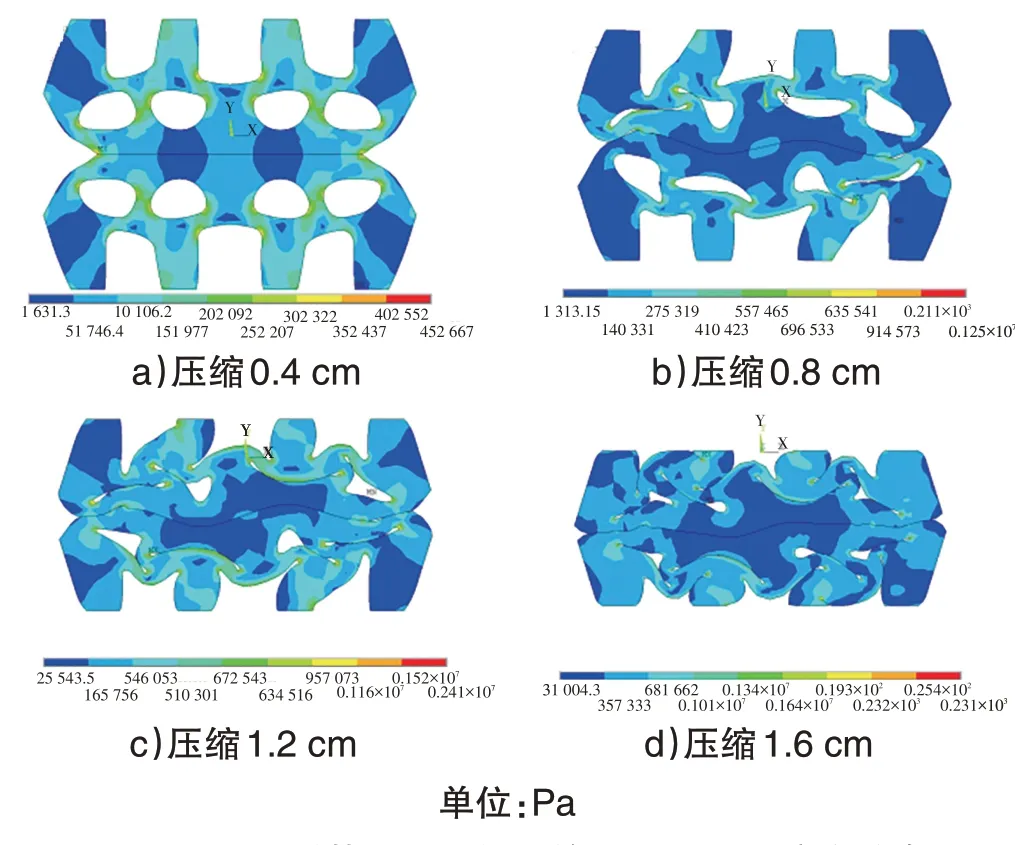
图7 工况1衬垫不同压缩量的Von-Mises应力分布

压缩量从0.4 cm 增加到1.6 cm 的过程中，橡胶密封衬垫的Von-Mises 应力最大值从0.45 MPa 增加到2.97 MPa，都出现在衬垫圆孔处，两个衬垫接触界面由于形变较小，Von-Mises应力小于圆孔处。工况2～5中密封衬垫的最大应力都出现在衬垫圆孔处，最大应力分别为2.84、2.72、3.00、3.12 MPa，两衬垫接触界面附近单元应力较小。不同错缝情况下，橡胶密封衬垫压缩量达到1.6 cm 时，衬垫最大Von-Mises 应力变化不大。

3.3 渗水路径接触应力

工况1中与路径相关的接触单元在密封衬垫压缩1.6 cm时的接触应力见图8。

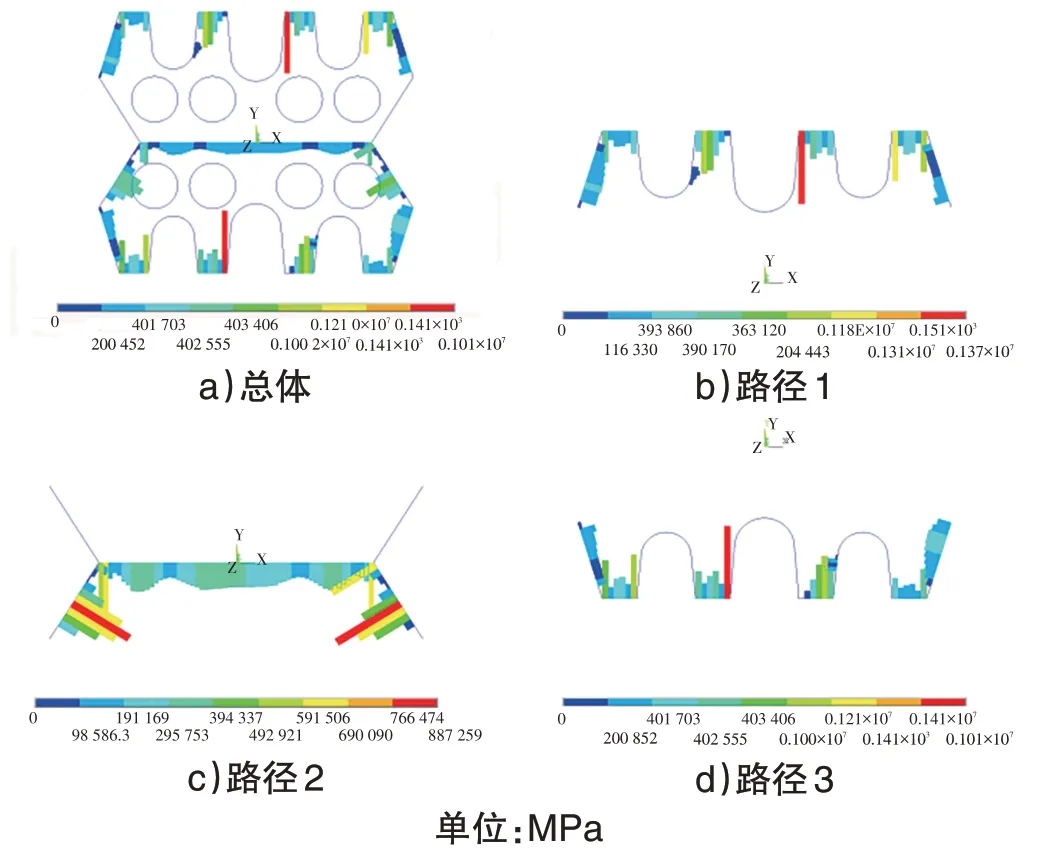
图8 工况1衬垫渗水路径接触应力

由图8可以看出，路径1和路径3沿途接触单元接触应力分布基本为中心对称方式且路径1 和路径3 接触单元接触应力峰值大于路径2沿途接触单元。路径1 接触应力峰值为1.77 MPa，路径2 接触应力峰值为0.89 MPa，路径3接触应力峰值为1.81 MPa；此时，橡胶密封衬垫的防水能力为0.89 MPa，控制路径为路径2。由路径2 的沿途接触应力可以看出，衬垫边缘处的接触应力明显大于中间接触面，在既有试验研究中，高水压情况下，当施加的静水压力处于密封衬垫防水临界压力值附近时，其水压值远大于密封衬垫中间接触面的接触压力，若在此基础上小幅度增加静水压力，则高水压透过边缘接触面进入接触面的内部，由于中间接触面的接触压力远小于此时的静水压力，故而发生接触面的急剧张开，因而在试验中会出现渗水突然剧烈喷出的现象。

工况1密封衬垫在不同压缩行程下各路径接触应力峰值变化见图9。

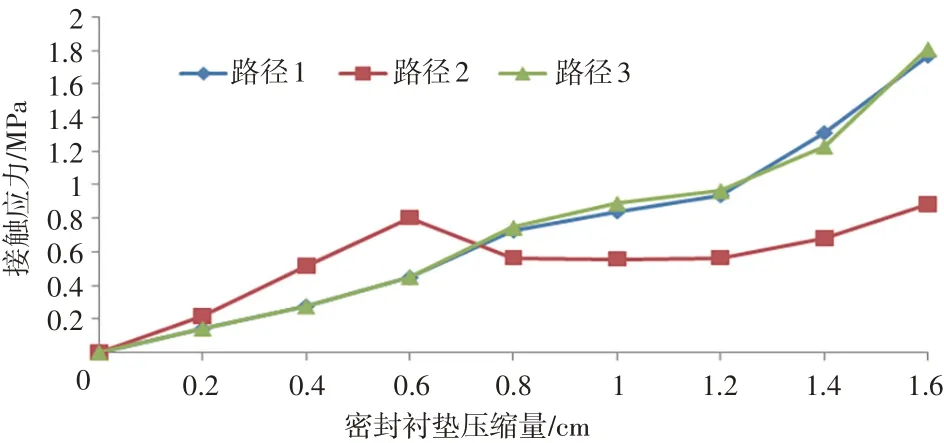
图9 工况1衬垫不同压缩行程接触应力峰值

各路径接触应力峰值基本随密封衬垫压缩量的增长而增长，路径1 和路径3 接触应力峰值基本保持一致，增长速率逐渐加快。路径2 接触应力在压缩0.6～0.8 cm 的过程中减小，随后增大，在压缩0.7 cm 前，密封衬垫防水性能由路径1和路径3沿途接触应力峰值控制，压缩超过0.7 cm后，防水性能由路径2沿途接触应力峰值控制。密封衬垫在压缩超过0.8 cm 后，控制路径的接触应力即达到0.4 MPa的防水要求。

工况2～5中橡胶密封衬垫不同压缩行程各路径接触应力峰值变化趋势与工况1基本一致，见图10。

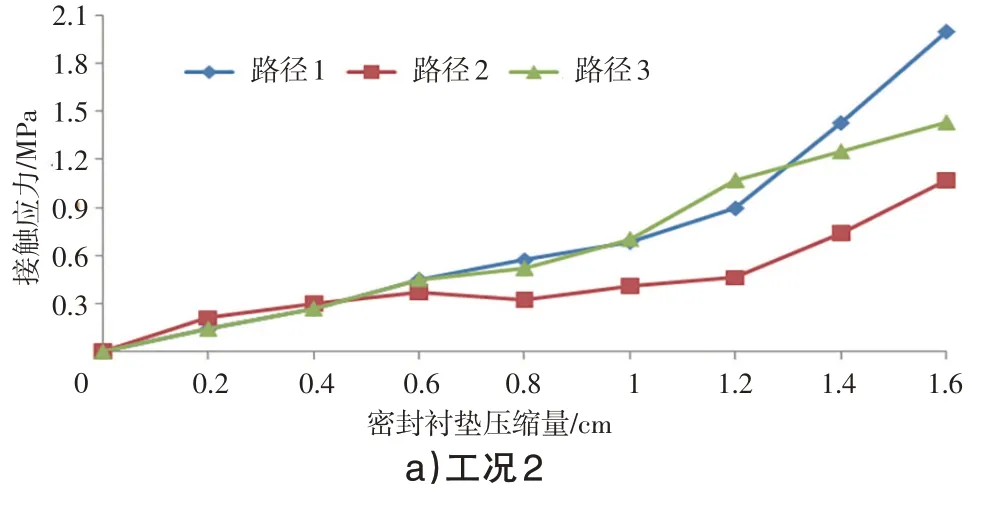
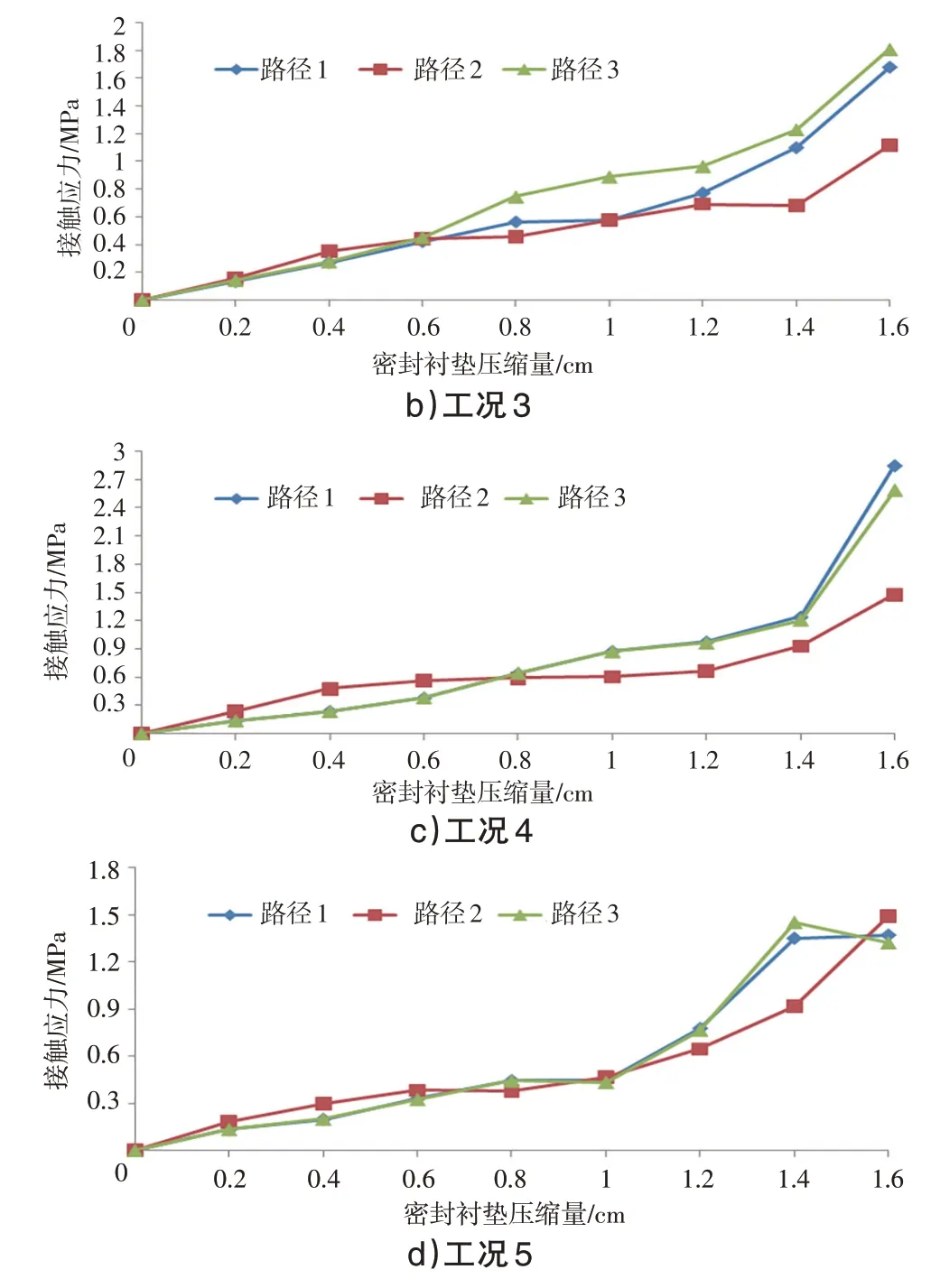
图10 工况2～5衬垫不同压缩行程各路径接触应力峰值

取不同工况密封衬垫不同压缩量时的防水性能控制路径接触应力峰值进行综合分析，见图11。

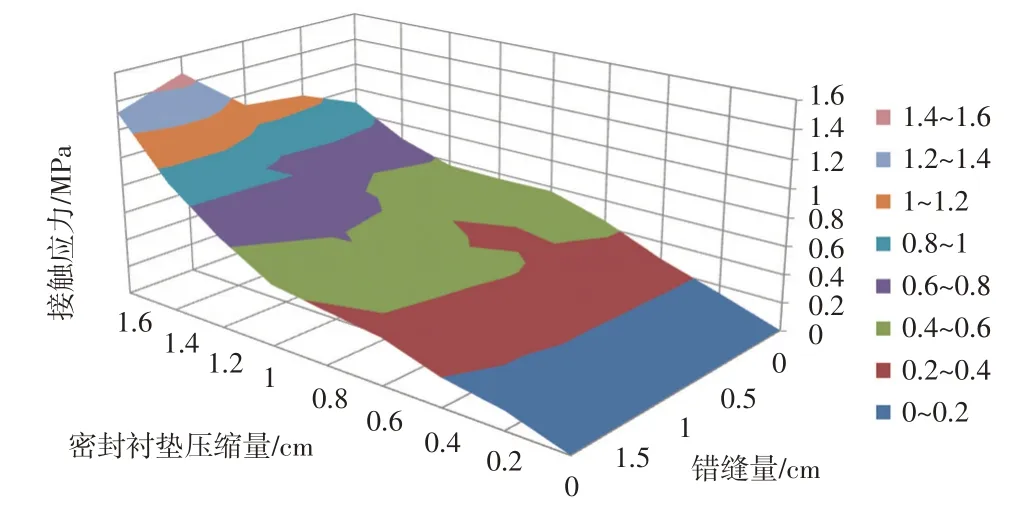
图11 不同工况和压缩量下衬垫控制路径接触应力峰值

由图11可以看出，密封衬垫压缩量为衬垫防水性能的主要影响因素，在理想的盾构管片拼装状态下，密封衬垫完全压缩至1.6 cm，获得控制路径最大的峰值接触应力，此时防水效果最好，防水压力达到0.88 MPa。密封衬垫压缩量＞0.8 cm，即衬砌接缝张开量＜0.8 cm，即可满足防水要求，这也符合GB 50446—2008《盾构法隧道施工与验收规范》对盾构隧道衬砌接缝0.8 cm张开量，1.5 cm错开量的限制规定。

一定范围内的错缝（＜2 cm）对密封衬垫控制路径峰值接触应力影响较小，在该范围内，随着错缝的增加，防水性能有一定幅度的增强，最大增强幅度为错缝1.5 cm时的67%。

3.4 密封衬垫整体压缩性能

已有对盾构隧道衬砌结构精细化建模分析研究中，在引入橡胶密封衬垫时，一般将其简化为具有非线性力学参数的弹簧或者均质的橡胶条，往往忽略密封衬垫内部的开孔和不规则几何形状对于衬垫力学性能的影响，因此需要对密封衬垫的力学性能在更为精细化建模的基础上进行分析。

选取工况1，即无错缝情况下密封衬垫模型的加载模拟结果，提取混凝土管片任一水平截面节点的竖向节点力之和，获得密封衬垫压缩量和密封衬垫对混凝土管片施加的竖向合力之间的关系，便于之后将密封衬垫简化为弹簧时的力学性能参数选取。拟合获得三次多项式，拟合度为0.996 42。见图12。

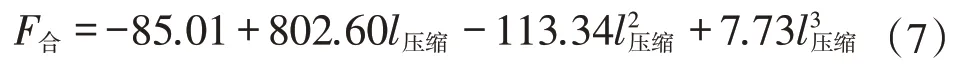
式中：F合为密封衬垫施加到混凝土管片的竖向合力，N；l压缩为密封衬垫压缩量，mm。

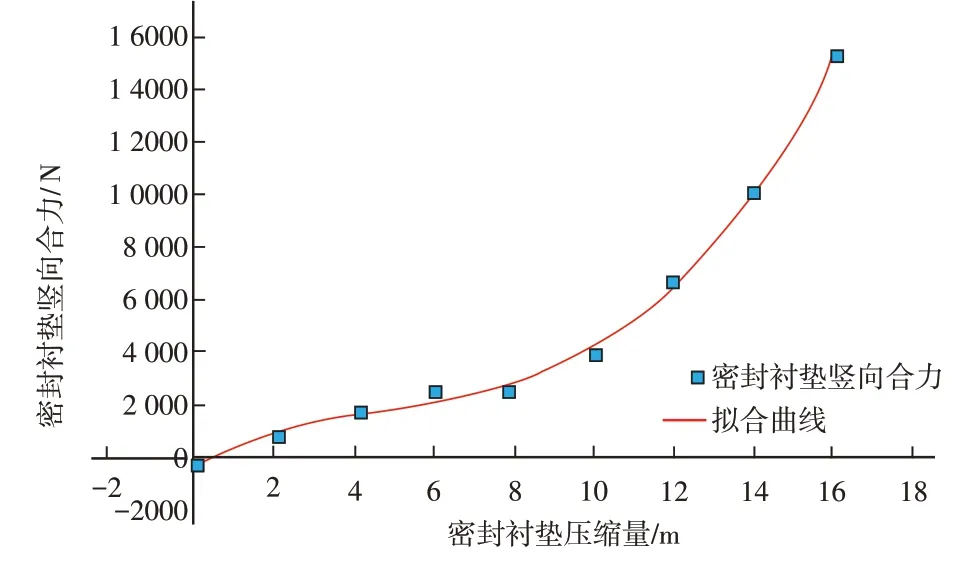
图12 压缩量和竖向合力拟合曲线

4 结论

1）在密封衬垫压缩的过程中，压缩量＜0.7 cm时，两个密封衬垫之间的接触应力峰值大于密封衬垫与衬砌之间的接触应力峰值，此时衬垫的防水性能由密封衬与衬砌之间的接触应力峰值决定，当压缩量＞0.7 cm时，两个密封衬垫之间的接触应力峰值小于于密封衬垫与衬砌之间的接触应力峰值，此时衬垫的防水性能两密封衬垫之间的接触应力峰值决定。

2）密封衬垫的防水性能受衬垫压缩量影响较大，受衬垫错开的影响较小，根据天津地铁10号线的实际工况，在满足GB 50446—2008 对衬砌接缝张开量0.8 cm 和错开量1.5 cm 的前提下，衬垫即可满足防水要求。

3）一定范围内的错缝（＜2cm）对密封衬垫的防水有一定程度的增强，最大增强幅度为错缝1.5cm 时的67%。

4）获得了天津地铁10 号线使用的密封衬垫压缩量和总压缩力之间的关系曲线和拟合式。