变算术解法束缚 立方程解法思路
2017-07-14张娟
张娟
[摘要]列方程解应用题作为一种重要的数学思想方法,同时也是教学难点,它对丰富学生解决问题的策略、提高解决问题的能力、发展数学素养有非常重要的意义。本文从提早孕伏、奠定基础,把握整体、探索规律,凸显对比、呈现优势,明确范围、灵活运用四种策略入手,探寻突破列方程解应用题这一教学难点的方法。
[关键词]数学教学 方程解法 教学策略
列方程解应用题作为一种重要的数学思想方法,它对丰富学生解决问题的策略,提高解决问题的能力,发展数学素养有着非常重要的意义。列方程解应用题,历来是教学中的难点,算术解法与方程解法的思路迥然不同,学生初学列方程解决实际问题时,往往不易摆脱长期运用的算术解法的束缚,难以寻求题中等量关系和形成方程解法的思路。为了突破难点,本文特介绍如下几项切实可行的措施。
一、提早孕伏奠定基础
分析数量关系是列方程解应用题的关键,培养学生寻找等量关系的能力是教学的重点。列方程时的数量关系与列算式时明显不同:列算式时的数量关系把已知和未知割裂,已知条件作为一方,要求的问题为另一方,通过已知数量的运算得到未知数量;而列方程的数量关系,把已知和未知融合起来,共同参与运算。
教学时可先安排一些能体现等量关系,有利于排除算术解法的干扰的习题,在组织练习时要有意识地为后面的教学做好孕伏和铺垫。如:
1.要求学生指明含字母的式子所表示的意义。例如:棉花种植组种了5亩水稻试验田,亩产是x斤。5x-总产量。
此形式的练习能帮助学生建立等量关系,若将箭头右边的数量具体化,则可布列方程。
2.从常见数量关系中寻找等量关系。例如,路程=时间×速度,工作总量=工作效率×时间,总价=单价×数量,以及各种体积、面积的计算公式等,经常性的复习一些常见的等量关系,有利于学生列方程时寻找等量关系。有时可以和表格法结合起来,效果更好。
3.训练学生把日常语言“翻译”为代数式。把日常语言“翻译”为代数式,是以数学语言为中介实现的。例如,“故事书比科技书的3倍多16本”,先翻译为数学语言“比某数的3倍多16”,再翻译为代数式,“3x+16”。其意义在于使学生真正明白每个代数式的实际意义,这不仅是学习方程的基础,也是培养学生把实际问题抽象为数学问题的能力。
4.要求学生根据题意,紧扣关键词,把应用题改写成文字题,再完成等式。例如,水果店有500斤苹果,卖了3筐,每筐x斤,还剩335斤。=335,紧扣“还剩”,得知“差”为335,写成文字题:500与x的3倍之差是335,得等式:500-3x=335。此练习是列方程解应用题的“前奏曲”。
二、把握整体探索规律
列方程解应用题题型丰富多样,归纳起来教学时可分为两大块进行:
1.人教版小学数学第九册第73页例1、例2共两例,可通过上述第4种练习形式,自然过渡到例题。如:先出示两道练习题:(1)学校图书馆买来27本文艺书和x本科技书,这两本书一共是50本。=50。(2)商店原来有74斤水果糖,又运来25斤,卖了x斤,还剩63斤。=63。让学生把方程写完整,再解出来,然后要求学生看书中例1、例2的解法,说出与练习的异同点。
2.有的题型可运用学生已熟练掌握的公式,布列方程,此类题解法易于理解。
(1)行程问题:速度×时间=路程
方程:45×x=270(求时间)
(2)面积问题:底x高÷2=三角形面积
方程:25×x÷2=100(求高)
(3)工程问题:工作效率×工作时间=工作量
方程:89×3+3x=387(求乙的工作效率)
三、凸显对比呈现优势
初学列方程,学生仍用已掌握的算术解法,对列方程解法很不适应,在教学中可通过例题分别用算术法和列方程进行分析解答,然后说明两种方法各自的特点,让学生自己进行比较,通过对比让学生自己认识到方程解法的优越之处。如此反复训练,学生就能排除由算术解法形成的思维方式的干扰,从而使学生逐步适应并熟练掌握方程解法,顺利达到从算术解法到列方程解法的过渡,逐渐体会到用字母代替数,认识到从算式到方程使我们有了更有利、更方便的数学工具,从算术方法到方程解法是数学的进步。
可见,方程解法的思路易于寻求。
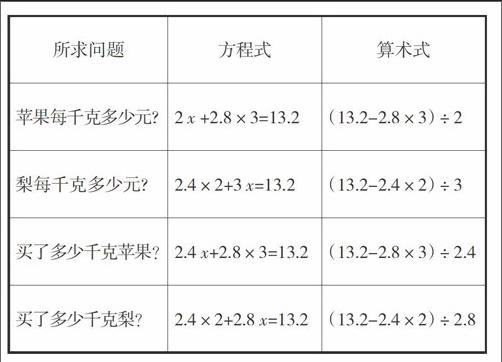
2.运用变题比較两种解法。以人教版小学数学第九册第77页例3为例,把梨的数量改为3千克,总价改为13.2元,将题中的问题改为已知量,然后逐一把某一条件变作问题,分别用两种解法列式。
可见,四个方程格式是一致的,其解题思路单一、简单,而所列四个算术各不相同,显然,方程解法优于算术解法。
四、明确范围灵活运用
在小学数学中,列方程解决实际问题,是在用算术方法解决实际问题的基础上进行教学的。由于数量关系的多样性和叙述方式上的不同,用算术方法解答实际问题,时常要用到逆思考,列式比较困难,解法的变化也比较多。用列方程的方法解决实际问题时,由于引进了字母表示未知数,一般不需要逆思考,可以使未知数和已知数直接参加列式运算,用未知数和已知数共同组成一个等式(即方程),然后解出未知数的值。这样思路直接,解法划一,可以化难为易,特别是在解答比较复杂,或有特殊解法的实际问题(如鸡兔同笼、和差、和倍、差倍)时,用方程往往比较容易。解答应用题时,应根据题目的特点选择合理的简便的解法。
1.逆思考的题宜用方程解;顺思考的题宜用算术解。例如,①五(1)班图书角原来有一些故事书,同学们又拿来18本,借出25本,还剩35本,原来有故事书多少本?②图书小组原来有42本故事书,同学们又拿来18本,借出25本,还剩多少本故事书?例①宜用方程法解,例②宜用算术法解。
2.凡是直接求几何图形的周长、面积的,宜用算术解;否则,宜用方程解。例如,求梯形的面积s,用算术解,列式为(a+b)·h÷2,若要求a、b、h中的某一个,则宜用方程解。
3.对于常见的三量关系,如:速度×时间=路程等,可写成:()×()=()的基本数量关系式,若求等式右边的数量,宜用算术解;若求等式左边某一数量,则宜用方程解。
