基于非线性破坏准则的地基临界荷载计算

欧阳志，鞠兴华

(陕西铁路工程职业技术学院，陕西渭南 714099)

基于非线性破坏准则的地基临界荷载计算

欧阳志，鞠兴华

(陕西铁路工程职业技术学院，陕西渭南 714099)

为计算基于非线性Mohr-Coulomb破坏准则影响下的条形基础地基临界荷载，通过“切线法”引入变量ct和φt，根据地基土体的极限平衡条件建立地基中任意一点处的应力平衡方程，给出了地基临界荷载p1/4的迭代计算方法，并结合算例计算分析了强度参数σt，c0和基础埋深d取不同值时非线性参数m对地基临界荷载的影响。结果表明，非线性破坏准则对地基临界荷载和塑性区的位置有重要影响；引入非线性破坏准则会明显减小临界荷载的计算值，并且zmax=b/4时的地基塑性变形区域更靠近于基础内侧。引入非线性破坏准则更符合地基实际，可更准确地评价承载力的大小。

地基基础工程；非线性破坏准则；条形基础；临界荷载；塑性区最低点位置；迭代法

地基临界荷载作为中国常用的地基承载力计算参数，一直以来都备受学术界和工程界关注。实践表明，在保证建筑物安全使用的情况下，是可以允许地基自基底以下一定深度范围内出现塑性区的[1]。地基中的塑性区首先从基底两侧的边缘处产生，然后分别向两侧和压密土楔顶点的方向发展，倘若基底以下塑性区的最大开展深度zmax达到基础宽度b的1/4时，对应的地基底部附加应力即为地基临界荷载p1/4。

在一般的土力学教材和资料上，地基临界荷载均是假定在k0=1.0和线性的Mohr-Coulomb强度条件下得到的，这与实际情况不符。假定k0=1.0是将地基中的自重应力视为静水压力状态，是对天然地基的人为加固，因此会过高估计地基的承载能力[2]；而土体发生剪切破坏时的大、小主应力通常情况下也为非线性的关系，线性关系仅仅是其中的一个特例[3]。文献[2]和文献[4—6]基于不同的弹性理论在假定k0≠1的条件下对地基临界荷载进行了研究，但是都没有考虑地基土发生剪切时，大、小主应力非线性关系的影响。文献[3]和文献[7]研究了非线性破坏准则与岩土材料地基承载力的关系。文献[8]基于二次型Mohr包络线对地基中塑性区的发展规律进行了研究。但关于非线性强度准则对地基临界荷载的影响规律，目前还未发现有研究。因此，本文根据非线性Mohr-Coulomb准则的“切线法”表达式[9-10]，建立地基中任意一点的应力平衡式，然后结合算例，对非线性破坏准则影响下地基临界荷载变化规律进行研究。

1 非线性Mohr-Coulomb破坏准则

在一般的土力学研究中，土体的剪切破坏大多假定服从线性的Mohr-Coulomb破坏准则(以下简称“MC准则”)。然而，大量的工程实践和实验研究表明[11-13]，在软弱围岩，尤其在土中，材料剪切破坏时的大、小主应力为非线性的关系，非线性关系表达式可用式(1)表示。式(1)通常被称为Power-Law准则，也称非线性MC破坏准则。

τ=c0(1+σn/σt)1/m，

(1)

式中：c0表示Mohr包络线与纵轴的截距；c0，σt均为岩土材料与剪切有关的参数。m决定了Mohr包络线的弯曲程度，当m=1.0时，式(1)表示线性的MC准则，c0和φ0=arctan(c0/σt)分别表示地基土的黏聚力和内摩擦角。但为保证曲线的外凸性，一般要求m>1.0。

将式(1)在坐标系中绘制曲线，如图1所示。

图1 非线性破坏准则曲线的切线Fig.1 Tangential line of envelop of nonlinear failure criterion

在图1所示的曲线型Mohr包络线上，任一点P处的切线方程可用式(2)表示。

τ=c1+σntanφt，

(2)

式中：ct，tanφt分别为图1中切线的截距和斜率。以φt为变量，ct，tanφt可表示为

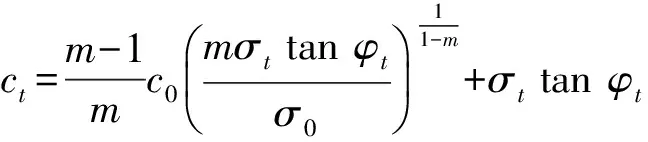
(3)

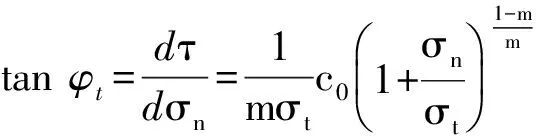
(4)

式(3)、式(4)中，σn表示该切点处的正应力。可以看出，土中某点处对应的抗剪强度与该点的正应力有关。因此，对于实际计算，应首先确定破坏面处某点的正应力σn，再由式(3)、式(4)可求出该点对应非线性MC破坏准则的ct，φt值。

下面用式(2)所示的Mohr包络线切线方程，来推导地基在条形受载时土中任一点处的应力平衡方程，进而对非线性参数m不同取值条件下的地基临界荷载变化规律进行研究。

2 基于非线性强度准则的临界荷载计算方法

如图2所示，假设条形基础的宽度为b，埋深为d，均布的基底附加应力为p0=p-γ0d。基础底面的接触压力为p，地基土的重度为γ0，土的静止侧压力系数为k0。借鉴前人的研究结果[2]，可知基底以下地基中M点处的总应力表达式为

(5)

式中：β=β1-β2；ψ=β1+β2；pm为考虑非线性强度准则时的基底附加应力。

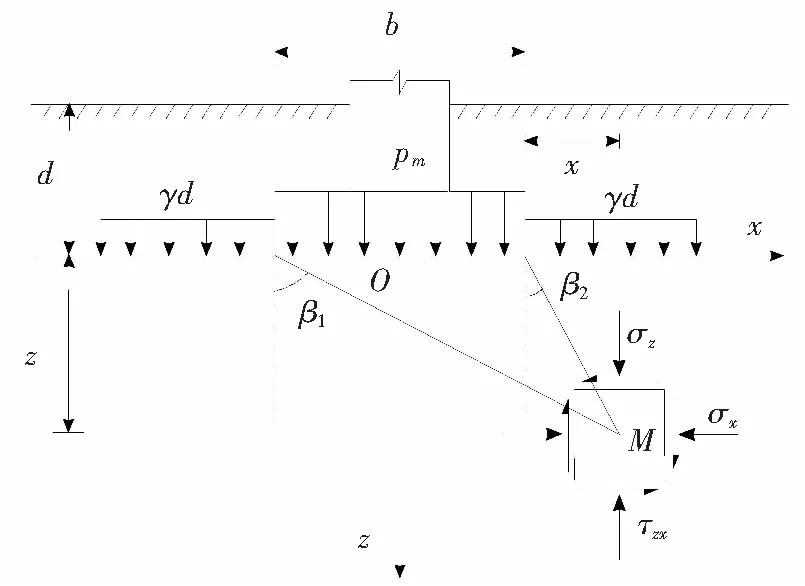
图2 条形均布荷载下地基内任一点总应力Fig.2 Total stress in ground under strip uniform distributed load

根据材料力学知识，可得M点处的大、小主应力为

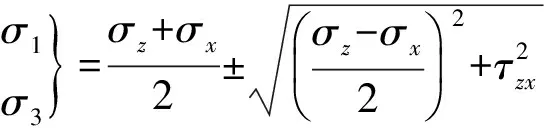
(6)

g1(pm)±g2(pm)。

(7)

式中：

根据非线性MC准则，土体的极限平衡条件可表示为

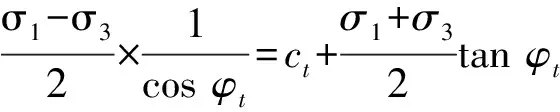
(8)

将式(7)代入式(8)，整理后可得

(9)

又由式(4)可得

g1(pm)-g2(pm)sinφt。

(10)

结合式(7)，对式(10)进行变换，可得

tanφt=

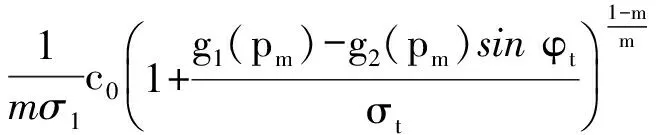
(11)

将pm代入式(11)，即可将式(11)转化为仅含有φt的一元方程表达式，由于一般的解析方法难以求解该方程，因此本文采用迭代法对φt进行计算。令

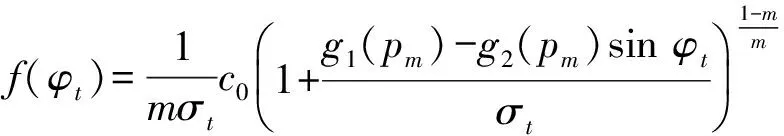
(12)

即可得到关于φt的一般迭代法表达式

(13)

迭代方法采用依次不断增大m值，不断更新迭代初始点的多次反复迭代，具体步骤如下。

对于给定的β，先假定m=1.1，在φn=φ0(φ0为基于线性MC准则时的地基土内摩擦角)处对式(13)开始进行迭代，当|φn+1-φn|≤10-4时，迭代停止，求出φm1和pm1；然后假定m=1.2，在φn=φm1处对式(13)进行迭代，当|φn+1-φn|≤10-4时，迭代停止，求出φm2和pm2；接下来每次对m增加0.1，在上一级m值条件求出的φm(n)处对式(13)进行迭代，然后再求出新的φm(n+1)和pm(n+1)，如此循环，直至求出给定m值时的φmt和pmt。

假定z=b/4，用β=arctan[(4x+4b)/b]-arctan[4x/b]替换式(9)中的β。由于基础两边的塑性区是对称的，故取基底以下地基的右半边考虑，令x在(-0.5b，0.5b)上以0.01b的等差取值，利用上述迭代方法求出各x坐标处的pm值，取其中的最小值作为此时地基的临界荷载p1/4。

3 非线性破坏准则对地基临界荷载的影响

3.1 基于非线性破坏准则的地基临界荷载计算值

算例1：有一个条形基础，宽b=4 m，地基土的重度γ0=γ=19 kN/m3，基础埋深d=3 m，地基土为一般黏性土，c0=30 kPa，σt=92.33 kPa，即当m=1时，φ0=18°，静止侧压力系数k0分别取1.0和1-sinφt[15]，非线性强度参数m在1.0～2.8上以0.2的等差取值，利用上述迭代方法分别计算m，k0在不同组合情况下的地基临界荷载p1/4和此时的临界夹角β，所得结果如图3、图4所示。

如图3所示，当k0一定时，p1/4随m增大而减小，且随着m的增大，p1/4刚开始减小得较快，之后越来越慢，此结论与文献[3]得到的地基极限承载力变化规律一致。结合图1可知，m的增大使得Mohr包络线呈非线性程度的增加，Mohr包络线向下弯曲，土体剪切破坏时的σ1-σ3减小，从而降低地基的承载能力；当m=1.8时，地基承载力分别降低了37.2%和30.6%，即采用非线性破坏准则对地基临界荷载的计算值有重要影响。

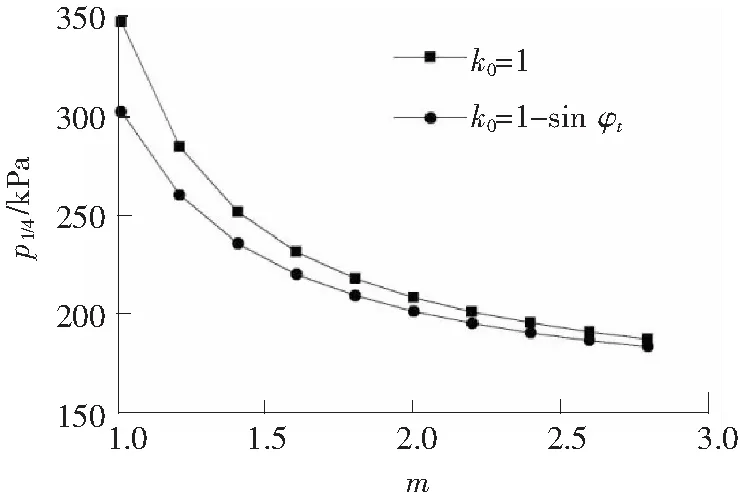
图3 不同k0值时p1/4与m的关系Fig.3 Relationship between critical load p1/4 and m under different coefficient k0

另外，从图3中还可看出，当m一定，k0=1.0时的p1/4计算值大于k0=1-sinφt的值，且两者之间的差值随m的增大而减小，结合式(5)可知，k0的减小将必然导致主应力关系式σ1+σ3的增大和σ1-σ3的减小，根据Mohr-Coulomb破坏准则，在其他条件不变的情况下，σ1+σ3的增大和σ1-σ3的减小均可使土体更容易发生剪切，以致于降低地基的承载力。当m=1.0时，本文所得结果与文献[2]方法得到的结果相等，也验证了本文方法的正确性。

由图4可知，临界夹角β随m的增大而增大，即图2中的x值不断减小。说明当基底应力达到临界荷载p1/4时，与以往所得结果β=π/2-φ0相比，随着Mohr包络线非线性参数m的增大，地基中塑性区最低点的位置将发生朝向基础内侧的方向移动，并且随着m的不断增大，塑性区最低点位置刚开始移动的较多，之后越来越少。由此可见，当考虑地基土的非线性破坏影响时，zmax=b/4时的地基塑性变形区域将更靠近基础的内侧，非线性破坏准则对地基塑性区的位置有重要影响。

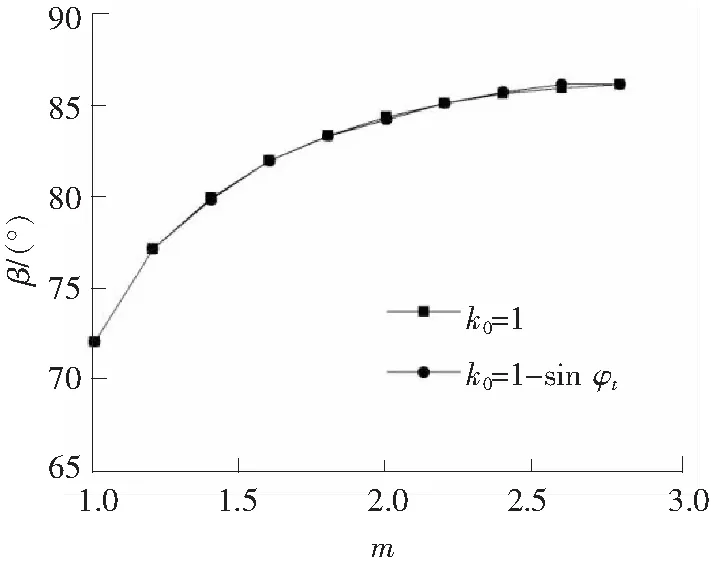
图4 不同k0值时β与m的关系Fig. 4 Relationship between critical angle β and m under different coefficient of k0

3.2 参数敏感性分析

1)参数φ0取不同值时非线性参数m对p1/4和β的影响

参数σt值取为285.43，141.14，92.33，67.38，51.96 kPa，分别对应当m=1时，φ0为6°，12°，18°，24°和30°，k0取1-sinφt，其他参数取值同算例1。用上述迭代方法分别计算φ0，m在不同组合条件下的地基临界荷载p1/4和此时的临界夹角β，计算结果如图5—图7所示。

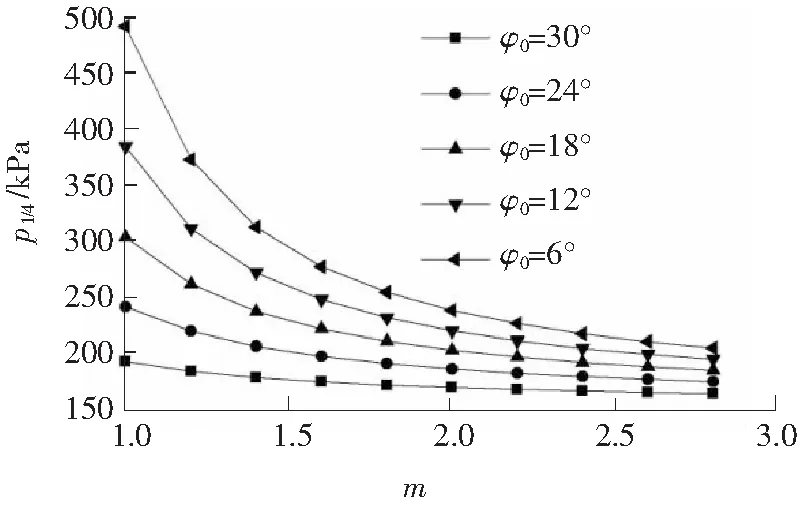
图5 不同φ0值时p1/4与m的关系Fig.5 Relationships between critical load p1/4 and m under different internal friction angle φ0

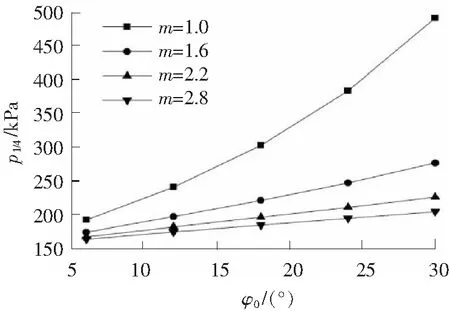
图6 不同m值时p1/4与φ0的关系Fig.6 Relationships between critical load p1/4 and internal friction angle φ0 under different m

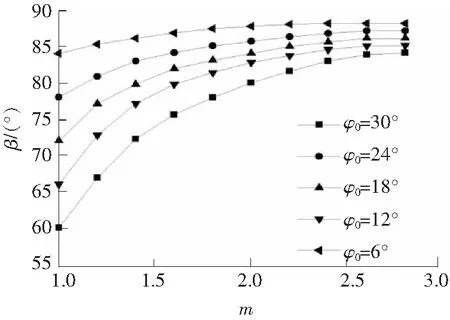
图7 不同φ0值时β与m的关系Fig.7 Relationships between critical angle β and m under different internal friction angle φ0

如图5所示，不同φ0条件下计算所得临界荷载p1/4均随m的增大而减小，并且其减小的速度均为刚开始较快，之后越来越慢。另外，φ0较大(或σt较小)时的p1/4减小速度明显大于φ0较小(或σt较大)时的，当φ0≤12°(或σt≥141.14 kPa)，m≥2.0时，曲线的变化规律几乎水平，临界荷载p1/4也近似为恒定值。当m从1.0增大到2.8时，φ0越大(或σt越小)，地基临界荷载降低的越多，说明当其他参数不变时，地基土的φ0越大，非线性参数m对地基临界荷载p1/4的影响越大。

从图6中可以看出，当m=1.0时，临界荷载p1/4随φ0的增加呈非线性增加的规律，与前人方法所得结果一致[2]；但随着非线性参数m的不断增加，p1/4随φ0的变化规律逐渐由非线性增加的曲线转变为线性增加的直线，且p1/4与φ0关系曲线的斜率也不断减小，说明Mohr包络线的非线性参数m越大，临界荷载p1/4随φ0增大的越缓慢。

如图7所示，不同φ0条件下计算所得临界夹角β均随m的增大而增大，其增加的速度均为开始较快，之后越来越慢。而且φ0较大(或σt较小)时的β值增加速度要大于φ0较小(或σt较大)时的，说明地基土的φ0越大(或σt越小)，非线性参数m对地基塑性区最低点位置的影响越大，对zmax=b/4时地基发生塑性变形的区域位置影响越大。

2) 参数c0取不同值时非线性参数m对p1/4和β的影响

c0取为10，20，30，40和50 kPa，k0=1-sinφt，其他参数取值同算例1。用上述迭代方法分别计算不同c0，m组合时的临界荷载p1/4和此时的临界夹角β，计算结果如图8、图9所示。

图8 不同c0值时p1/4与m的关系Fig.8 Relationships between critical load p1/4 and m under different cohesive force c0

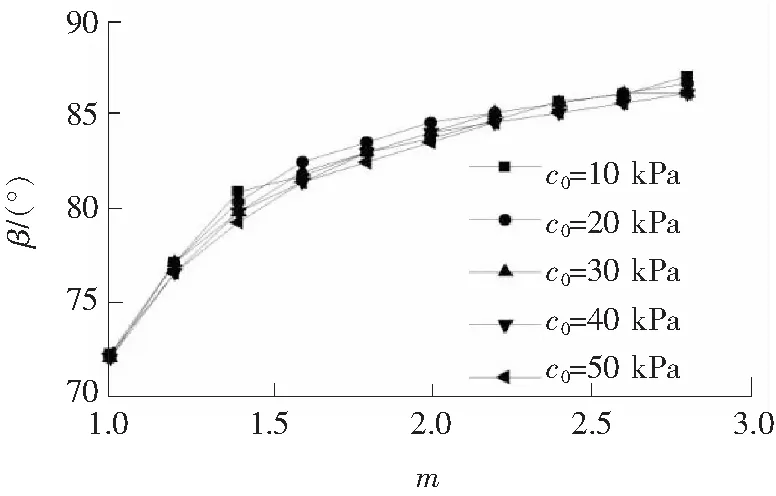
图9 不同c0值时β与m的关系Fig.9 Relationships between critical angle β and m under different cohesive force c0

如图8所示，在不同的c0条件下计算所得p1/4均随m的增大而减小，其减小的速度也均为刚开始较快，之后越来越慢。在不同的c0条件下，p1/4随m的变化规律几乎相同，说明当其他参数一定时，无论地基土的c0有多大，Mohr包络线的非线性参数m对地基临界荷载p1/4的影响规律都不变。另外，当m值一定时，所得p1/4随c0的变化规律均为线性地增加，且对于不同的m值，p1/4随c0增大的单位增量几乎相同，说明非线性参数m的变化并不影响p1/4与c0的关系。

如图9所示，不同σt值条件下计算所得临界夹角β均随m的增大而增大，其增加的速度均为刚开始较快，后来越来越慢。不同c0条件下的β与m关系曲线都近乎重合，说明当其他参数一定时，无论地基土的c0有多大，非线性参数m对地基中塑性区最低点位置的影响规律都不变。

3) 埋深d取不同值时非线性参数m对p1/4和β的影响

埋深d值取为1，2，3，4和5 m，k0=1-sinφt，其他参数取值同算例1。用上述迭代方法分别计算不同d，m组合时的临界荷载p1/4和此时的临界夹角β，计算结果如图10、图11所示。

如图10所示，不同基础埋深d条件下计算所得p1/4均随m的增大而减小，其减小的速度也均为刚开始较快，后来越来越慢。不同d条件下所得p1/4随m的变化规律几乎相同，说明当其他参数一定时，无论d有多大，非线性参数m对地基临界荷载p1/4的影响规律都不变。另外，当m值一定时，所得p1/4随d的变化规律均为线性地增加，且对于不同的m值，p1/4随d增大的单位增量几乎相同，说明Mohr包络线的非线性参数m的变化并不影响p1/4与d的关系。

图10 不同基础埋深时p1/4与m的关系Fig.10 Relationships between critical load p1/4 and m under different load embedded depth

如图11所示，不同埋深d条件下计算所得β均随m的增大而增大，其增加的速度刚开始较快，后来越来越慢；不同d值条件下的 β与m关系曲线也都近乎重合，说明当其他参数一定时，无论d有多大，非线性参数m对地基中塑性区最低点位置的影响规律都不变。

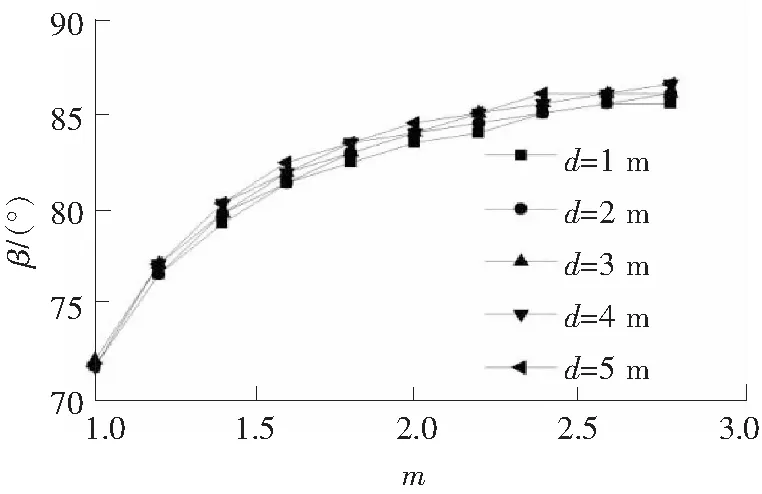
图11 不同基础埋深时β与m的关系Fig.11 Relationships between critical angle β and m under different load embedded depth

4 结 论

1)非线性破坏准则对地基临界荷载和塑性区的位置有重要影响。

2)与采用线性破坏准则相比，引入非线性强度准则会明显减小地基临界荷载p1/4的计算值，并且zmax=b/4时地基中塑性变形区域将更靠近于基础的内侧。

3)p1/4随非线性参数m增大而减小，并且随着m的增大，p1/4刚开始减小的较快，之后越来越慢；地基中塑性区最低点位置也随m的增大，刚开始移动的较多，之后越来越少。

4)强度参数φ0越大，非线性参数m的变化对p1/4的影响越显著，并且m越大，p1/4与φ0关系曲线的斜率越小。但无论基础埋深d和强度参数c0有多大，参数m对p1/4的影响规律都几乎不变；无论m有多大，p1/4随c0或p1/4随d的变化规律都不变。

5)φ0越大，非线性参数m的变化对zmax=b/4时地基塑性区的位置影响越显著；但无论c0，d取多大，参数m对此时地基塑性区位置的影响规律都不变。

6)本文论证分析的不足之处是没有具体的工程实例，且缺少实测结果资料用于验证。在以后的研究中将应用本文方法求得的地基承载力特征值与承载力测试结果对比分析，验证计算结果，进一步完善理论分析方法。

/References:

[1] 本书编委会. 建筑地基基础设计规范理解与应用[M]. 2版.北京: 中国建筑工业出版社, 2012: 85.

[2] 隋凤涛, 王士杰, 马建超. 新的临界荷载计算公式[J]. 河北农业大学学报, 2009, 32(5): 94-97. SUI Fengtao, WANG Shijie, MA Jianchao. New formula of critical load of subsoil[J]. Journal of Agricultural University of Hebei, 2009, 32(5): 94-97.

[3] 杨小礼, 郭乃正, 李亮. 非线性破坏准则与岩土材料地基承载力研究[J]. 岩土力学, 2005, 26(8): 1177-1183. YANG Xiaoli, GUO Naizheng, LI Liang. Bearing capacity of a strip footing with nonlinear failure criterion[J]. Rock and Soil Mechanics, 2005, 26(8): 1177-1183.

[4] 陈乐意, 李镜培, 梁发云. 考虑荷载埋深与K0变化的地基临界荷载[J]. 岩土工程学报, 2010, 32(12): 1930-1934. CHEN Leyi, LI Jingpei, LIANG Fayun. Critical load of ground considering load embedded depth and variation ofK0[J].Chinese Journal of Geotechnical Engineering, 2010, 32(12): 1930-1934.

[5] 陈燕, 彭超, 梅岭. 考虑应力状态的圆形基础地基承载力参数分析[J]. 江苏科技大学学报(自然科学版), 2016, 30(5): 513-516. CHEN Yan，PENG Chao，MEI Ling. Analysis of parameters for the bearing capacity of subsoil of circular foundation with consideration of stress states[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2016, 30(5): 513-516.

[6] 曹耿, 余安琴, 余兴平. 条形均布荷载下地基临界荷载分析[J]. 低温建筑技术, 2014, 36(9): 145-147.

[7] YANG X, YIN J H, LI L. Influence of a nonlinear failure criterion on the bearing capacity of a strip footing resting on rock mass using a lower bound approach[J]. Canadian Geotechnical Journal, 2003, 40(3): 702-707.

[8] 李顺群, 王英红, 柴寿喜，等. 二次曲线作为Mohr包线时的地基塑性区[J]. 广西大学学报:自然科学版, 2009, 34(3): 297-300. LI Shunqun, WANG Yinghong, CHAI Shouxi, et al. Determination of critical edge pressure and plastic zone for subsoil considering quadratic curve as mohr envelop[J]. Journal of Guangxi University: Nat Sci Ed, 2009, 34(3): 297-300.

[9] 唐高朋, 李亮, 赵炼恒,等. 非线性破坏准则下边坡稳定性极限分析斜条分法[J]. 岩土力学, 2015, 36(7): 2063-2072. TANG Gaopeng，LI Liang，ZHAO Lianheng，et al. Inclined slices method for limit analysis of slope stability with nonlinear failure criterion[J]. Rock and Soil Mechanics, 2015, 36(7): 2063-2072.

[10]ZHAO L, LI L, YANG F, et al. Upper bound analysis of slope stability with nonlinear failure criterion based on strength reduction technique[J]. Journal of Central South University of Technology, 2010, 17(4): 836-844.

[11]LADE P V, DUNCAN J M. Elastoplastic stress-strain theory for cohesionless soil[J]. Journal of the Geotechnical Engineering Division, 1975, 101(1): 1037-1053.

[12]AGAR J G, MORGENSTERN N R, SCOTT J D. Shear strength and stress-strain behaviour of Athabasca oil sand at elevated temperatures and pressures[J]. Canadian Geotechnical Journal, 1985, 24(1): 1-10.

[13]LABUZ J F, ZANG A. Mohr-Coulomb failure criterion[J]. Rock Mechanics and Rock Engineering, 2012, 45(6):975-979.

[14]现代工程数学编委会. 现代工程数学手册(第1卷)[M]. 武汉: 华中工学院出版社, 1985: 30.

[15]JAKY J. The coefficient of earth pressure at rest[J]. Journal of the Society of Hungarian Architects and Engineers, 1944, 21(3): 211-221.

Critical load calculation of foundation based on nonlinear failure criterion

OUYANG Zhi, JU Xinghua

(Shanxi Railway Institute, Weinan, Shanxi 714099, China)

In order to calculate the critical load of strip footing under a nonlinear Mohr-Coulomb failure criterion, the variablesctandφtare created by a generalized tangential technique, the equilibrium equation of total stress at any point in the foundation is established according to the limit equilibrium condition of subsoil, and a iterative calculation method of critical loadp1/4of the foundation is presented. Through an sample, the effect of differentmon the critical load of the foundation when the strength parametersσt,c0and footing embedded depth d take different values is calculated. The results show that nonlinear failure criterion has important influence on the critical load and the location of plastic zone in the foundation. Using nonlinear Mohr-Coulomb failure criterion could decrease the calculated value of the critical load, and the location of plastic zone of the foundation is closer to the center line whenzmax=b/4.Theintroductionofnonlinearfailurecriterioncanbetterconformtothefoundationrealityandaccuratelyevaluatethebearingcapacity.

groundfoundationengineering;nonlinearfailurecriterion;stripfooting;criticalload;positionoflowestpointatplasticzone;iterativemethod

1008-1534(2017)04-0259-06

2017-04-25;

2017-05-25；责任编辑：冯 民

陕西省教育厅科研项目(15JK1169)

欧阳志(1983—)，男，陕西渭南人，讲师，硕士，主要从事道路路基病害防治方面的研究。

E-mail:ouyangzhi.good@163.com

TU443

A

10.7535/hbgykj.2017yx04005

欧阳志，鞠兴华.基于非线性破坏准则的地基临界荷载计算[J].河北工业科技,2017,34(4):259-264. OUYANG Zhi, JU Xinghua.Critical load calculation of foundation based on nonlinear failure criterion[J].Hebei Journal of Industrial Science and Technology,2017,34(4):259-264.