非合作信号射频域干扰抵消性能分析

王天宇，孙志刚，郑淑梅

(中国电子科技集团公司第五十四研究所，河北石家庄 050081)

非合作信号射频域干扰抵消性能分析

王天宇，孙志刚，郑淑梅

(中国电子科技集团公司第五十四研究所，河北石家庄 050081)

针对航空测控系统面临宽带干扰时，缺乏有效的抗干扰手段的问题，研制了定向天线和全向天线的接收结构，可在射频域抵消外来的非合作信号，以保证合作信号的准确接收。并讨论了单抽头和多抽头两种结构模型。利用干扰抵消算法，以剩余非合作信号功率最小为准则，进行了理论推导。并提出在多抽头结构的工程实现中采用矢量调制器来进行幅度和相位的调整。仿真结果表明：对于单抽头结构，在2.6 GHz频段，对于带宽100 MHz的信号，当延迟线长度调整误差为2%时，最优的干扰抑制能力达到了45 dB，当考虑幅度调整误差为10%时，干扰抑制能力会降低约10 dB；对于多抽头结构，使用与单抽头相同的信号。以双抽头为例，当传输时延差固定时，最优干扰抑制能力可达81 dB，仿真结果从理论上验证了接收结构的可行性。

无线通信技术；射频域干扰抵消；单抽头；多抽头；矢量调制器；延迟线

在航空测控系统中，经常面临着非合作信号的干扰问题，如何确保合作信号准确地接收是被关注的重点问题，当面临宽带高阻塞式干扰时，现有的抗干扰手段效果不佳[1-2]，自适应干扰抵消技术是解决该问题的新途径。

自适应干扰抵消算法的理论基础来源于1967年WIDROW等[3]早先对自适应噪声对消理论的研究，以及LMS算法。LMS算法简单、易于实现、运算量小，针对干扰抵消系统，采用LMS算法的模拟实现较为合适[4-5]。GLOVER[6]研究了自适应噪声对消系统的频域特性，给出了系统的频域近似模型，后来杜武林[7]跟踪研究了自适应干扰对消技术，指出了该技术的原理、关键技术以及在军事通信应用中的重要意义，郑伟强等[8]讨论了开环前馈和闭环反馈的干扰对消系统。

现有的干扰抵消算法，都需要测向天线测量出接收信号的入射角度，利用阵列接收天线改变天线方向图，在非合作信号方向形成零陷，从而达到干扰抵消的效果，目前盲多波束形成算法也有广泛应用，能够快速收敛到不同的信号，解决了盲多波束系统中对同一信号重复收敛的问题[9-13]。本文提出的干扰抵消算法是一种不需要测向的盲抵消算法，利用不同接收天线接收到信号的信干比不同，进行幅度和相位的调整，完成干扰抵消的工作。

针对测控系统中面临的宽带高阻塞式干扰[14-15]，提出了定向天线为主接收天线，全向天线为辅助天线的接收结构，通过调整全向天线接收的非合作信号来抵消定向天线接收的非合作信号，从而保证合作信号的准确接收。分别讨论了单抽头[16]和多抽头[17]的抵消结构模型，以剩余非合作信号功率最小为准则，进行了理论推导，进一步进行了仿真验证，对于单抽头结构采用延迟线及衰减器来进行相位、幅度的调整[18-19]，在仿真时考虑了幅、相调整误差对于干扰抵消性能的影响，还对带宽内各频率分量的干扰抵消能力进行了测试。对于多抽头结构采用矢量调制器[20-21]来进行相位、幅度的调整，以双抽头为例进行了仿真分析，验证了带宽、多径时延差等对多抽头干扰抵消效果的影响。本文的研究结果为后续硬件实现提供了理论支持和性能的评估。

1 干扰抵消基本原理

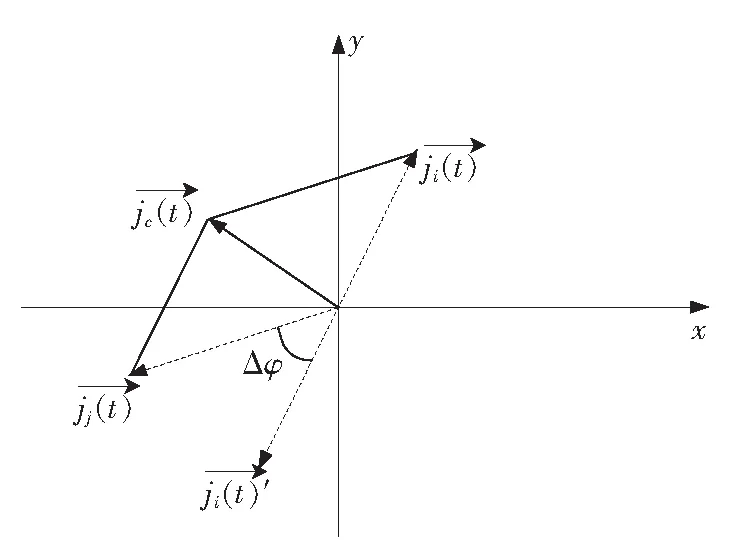
图1 非合作信号矢量抵消原理图Fig.1 Schematic diagram of non-cooperative signal vector cancellation

令定向天线和全向天线接收的非合作信号分别为

ji(t)=hicos (wt+φi)，

(1)

jj(t)=hjcos (wt+φj)。

(2)

两路信号相加后

jc(t)=ji(t)+jj(t)=

hicos(wt+φi)+hjcos(wt+φj)=

hcos(wt+φ)，

(3)

式中：

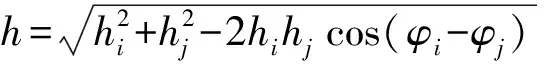
(4)

对式(4)求h关于hi的偏导数，可得：

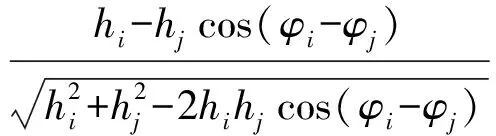
(5)

hi-hjcos(φi-φj)=0。

(6)

同样求h关于φi的偏导数

(7)

hihjsin (φi-φj)=0。

(8)

因为hihj≠0，所以

sin(φi-φj)=0，

(9)

即φi-φj=π-Δφ，代入式(9)得：

sin(Δφ)=0，

(10)

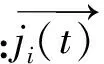
2 系统模型

2.1 单抽头干扰抵消结构

单抽头结构常用来抑制能量足够强的一条多径非合作信号(见图2)。定向天线接收来自远场信号，接收机接收到的信号x1(t)可以表示为

x1(t)=s(t)+ji(t)+n(t)，

(11)式中：ji(t)为远端传来的非合作信号；n(t)是能量为En的加性白高斯噪声；s(t)为远端传来的合作信号。

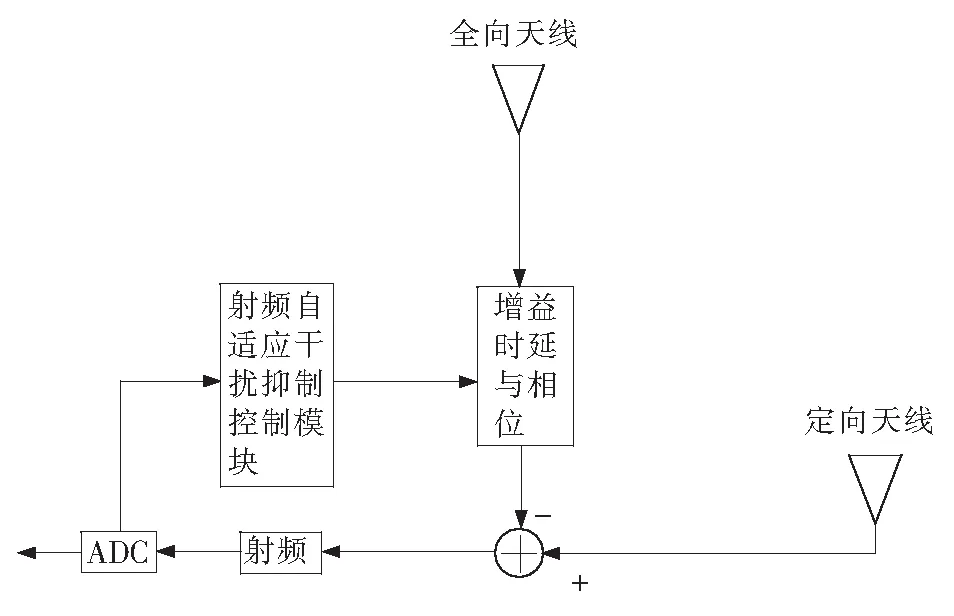
图2 单抽头干扰抑制模型Fig.2 Single tap interference cancellation model

在分析单抽头结构的干扰抑制性能时，定向天线和全向天线接收的非合作信号分别为

ji(t)=hij(t-τi)+n(t)，

(12)

jj(t)=hjj(t-τj)+n(t)，

(13)

式中：j(t)为非合作信号发射机的输出信号；hi,hj为信道增益；τi,τj为信道延迟。

将全向天线接收信号通过长度可调的延迟线和衰减器进行相位、幅度的调整后，得到重建定向天线接收的非合作信号jc(t)(简称干扰重建信号)，通过定向天线射频接收信号x1(t)与干扰重建信号jc(t)相减，达到干扰抑制的目的：

jc(t)=αcjj(t-τc)，

(14)

式中：αc表示衰减器的幅度因子；τc表示延迟系数。

经过射频域干扰抑制后，残余非合作信号jr(t)可表示为

jr(t)=jc(t)-jj(t)。

(15)

残余jr(t)的能量，决定着模拟域干扰的抑制能力。以残余非合作信号jr(t)能量最小为目标，定义目标函数Λ为

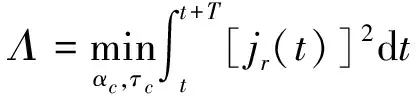
(16)

式中：T为控制器跟踪控制(能量检测)周期。

定义干扰抑制能力G[22-23]为

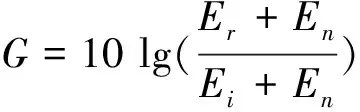
(17)

单位为dB。其中，Er为残余干扰信号jr(t)的能量；Ei为定向天线接收的干扰信号ji(t)的能量；En为噪声能量。从定义可以看出，G为负值，G越小，干扰抑制能力越强。

2.2 多抽头干扰抵消结构

图3 多抽头干扰抑制模型Fig.3 Multi-tapinterference cancellation model

依据傅里叶变换规则，对于定向天线实际干扰信道的频率响应Hc(f)为

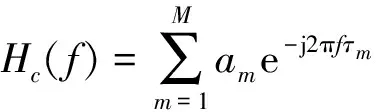
(18)

同理，对于全向天线实际干扰信道的频率响应He(f)为

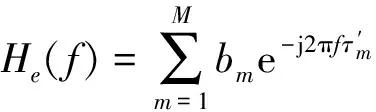
(19)

类似的，图3中多抽头干扰估计结构的频率响应Hs(f)可以写为

(20)

进一步，将式(20)中的结果重写为向量乘积的形式

(21)

其中权矢量W、频点f的相位旋转因子矢量X(f)分别定义为

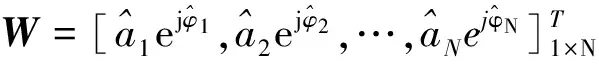
(22)

(23)

得到干扰抵消后的等效剩余非合作信号频响Hr(f)：

Hr(f)=Hc(f)-Hs(f)He(f)。

(24)

则干扰抵消后的剩余非合作信号功率谱密度Sr(f)为

Sr(f)=|Hr(f)|2Sl(f)。

(25)

其中Sl(f)表示非合作信号发送射频信号的功率谱密度。

假设非合作信号发射机采用sinc函数作为发射信号的成形脉冲函数，则本地发送射频信号的功率谱密度在信号带宽B内是平坦的，且信号带宽为基带符号速率的倒数：

(26)

结合式(25)、式(26)，剩余自干扰信号的总功率Pr为

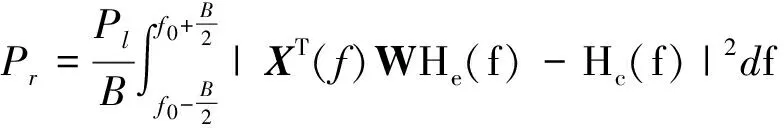
(27)

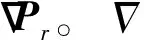
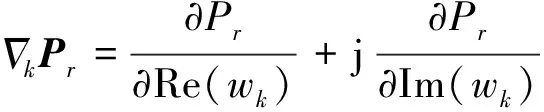
(28)

当复值梯度向量的实部、虚部均为0时，剩余干扰功率Pr取得极值。按照式(28)给出的复值梯度向量，对剩余干扰功率Pr求梯度得到：

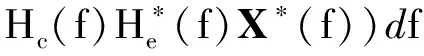
(29)

其中矩阵R、向量Q分别定义为

(30)

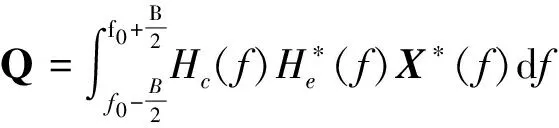
(31)

结合式(19)、式(23),化简矩阵R、向量Q：

(32)

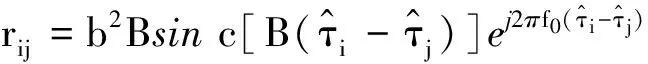
(33)

式中：qn为向量Q中的第n个元素；rij为矩阵R中第i行第j列元素；sinc(·)函数的定义如式(34)所示：

(34)

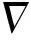
Wopt=R-1Q。

(35)

结合矩阵R、向量Q的表达式将信号功率化简为

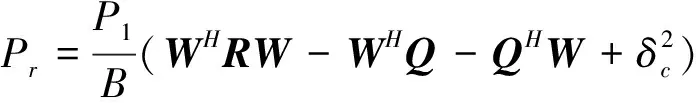
(36)

其中:

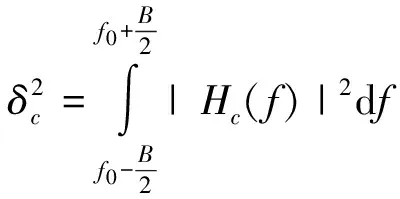
(37)

将Wopt带入到Pr表达式中，得到:

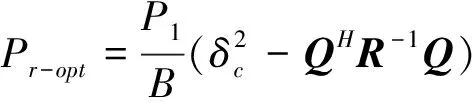
(38)

因此，Pr-opt为射频域多抽头干扰抵消后的最小剩余干扰功率。进一步，定义干扰抑制比表示干扰抵消前后的干扰信号功率之比，则多抽头干扰抵消结构的最大干扰抑制比ISR 表示为

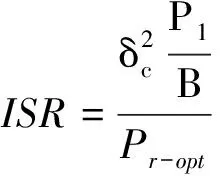
(39)

可以看出与单抽头结构抑制比定义不同，多抽头结构干扰抑制比均为正值。

因此，考虑单径干扰信道场景，双抽头干扰抵消结构的最大干扰抑制

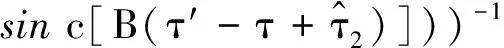
(40)

其中，参数γ，β分别定义为

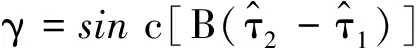
(41)

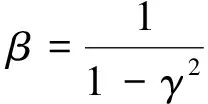
(42)

可以看出针对单径干扰信号的双抽头干扰抵消结构，其最优权矢量由干扰信号带宽、载波频率以及抽头时延与干扰传输时延之差决定；其最佳的干扰抑制效果与干扰信号带宽、抽头时延与干扰传输时延之差有关。

3 数字与仿真结果

3.1 单抽头结构仿真结果

本文假设条件如下：载波频率为2.6 GHz，接收干扰信号能量Ei比噪声能量En高90 dB，定向天线和全向天线接收信号时延差为1 ns，经计算得最佳的延迟线长度为1.5 m。

当考虑延迟线长度调整误差时，可以得到图4所示的不同带宽下干扰抑制能力与延迟线调整误差的关系。

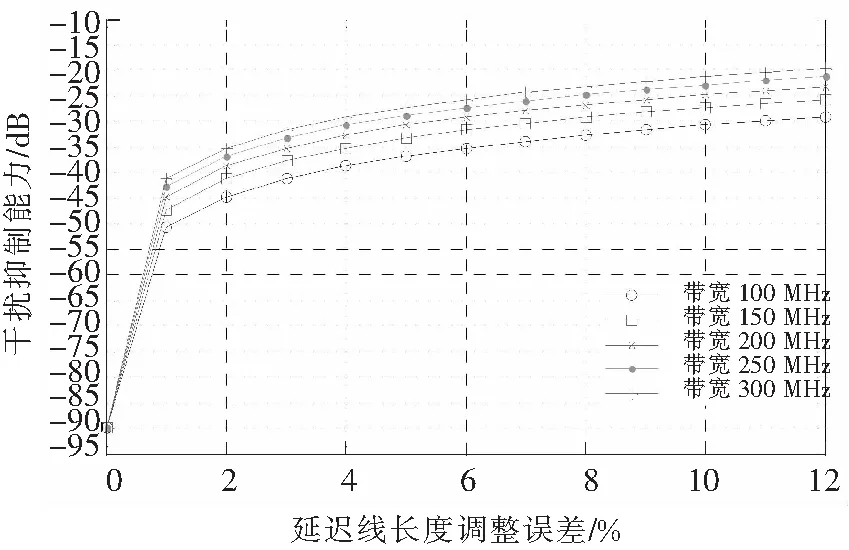
图4 不同带宽下干扰抑制能力与延迟线调整误差的关系Fig.4 Relationship between interference cancellation and delay line error in different bandwidth

从图4可以看出，在2.6 GHz频段，对于带宽100 MHz的信号，当延迟线长度调整误差为2%时，干扰抑制能力达到了45 dB。可得出如下规律：

1) 带宽固定不变时，干扰抑制能力随着相位误差的增大而减小；

2) 干扰抑制能力固定时，带宽越宽，对相位调整的精度要求越高；

3) 相位调整误差固定时，干扰抑制能力随带宽的增加而下降。

接下来考虑不同延迟线误差条件下信号带宽内各频率分量的干扰抑制情况，以带宽100 MHz、频段2.6 GHz为例，各频率分量的干扰抵消能力与相位误差的关系如图5所示，图中横坐标中心点0代表着中心频点2.6 GHz，左右两边各点代表着带宽内其他频点。

图5 各频率分量的干扰抑制能力与延迟线误差之间的关系Fig.5 Relationship between each frequency component interference cancellation and delay line error

从图5可以看出，当不存在延迟线误差时，带宽内各频率分量的干扰抵消能量为90 dB，在带宽内近似平坦地抑制，残余干扰降至噪底；当延迟线误差为1%时，非合作信号带宽边缘处的干扰抵消能量约为33 dB，带宽中心可抵消90 dB的干扰，带宽内能量波动幅度约为67 dB。可得出如下规律：

1) 载波中心频率处的干扰抑制能力最好，非合作信号宽带边缘处的频率分量干扰抑制能力效果较差；

2) 在带宽范围内，频率跨度越大，频率分量干扰抑制能力效果差别越大；

3) 干扰抑制能力随着，相位误差的变化而变化，各频率分量的干扰抑制能力也不相同。

考虑幅度调整误差对干扰抵消能力的影响，假定延迟线长度调整误差约为2%时，关系如图6所示。

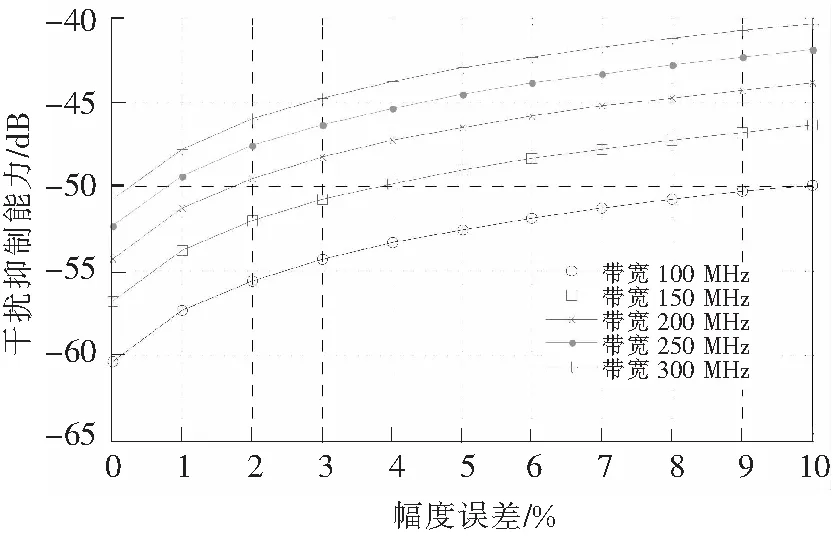
图6 不同带宽条件下干扰抑制能力与幅度误差关系Fig.6 Relationship between interference cancellation and amplitude error in different bandwidth

从图6中可以看出，带宽为100 MHz的信号，10%的幅度调整误差会使干扰抵消能力降低约10 dB。可得出如下规律：

1) 带宽固定时，干扰抑制能力随幅度调整误差的增加而降低；

2) 带宽越宽，幅度调整误差的影响效果越小。

3.2 多抽头结构仿真结果

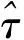
图7 不同抽头时延下，双抽头结构干扰抵消性能Fig.7 Double tap interference cancellation performance in different tap delay

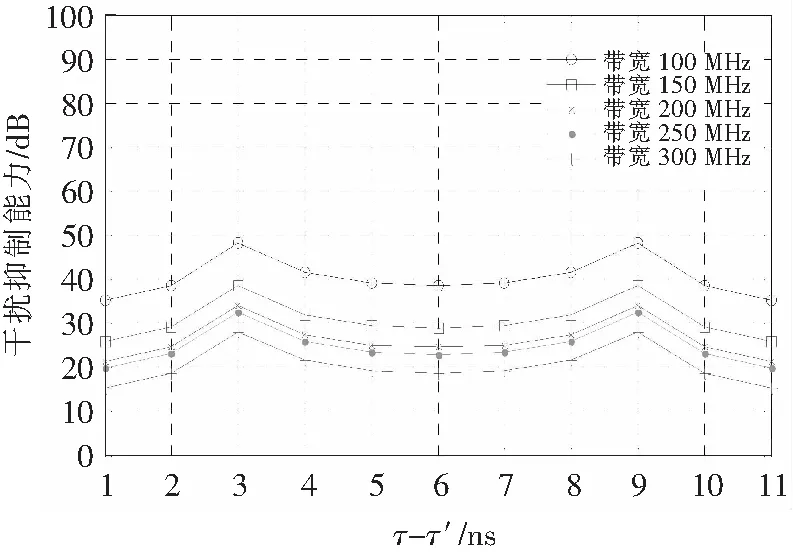
图8 不同干扰信号带宽下，双抽头结构干扰抵消性能随传输时延差的变化Fig.8 Variaton of interference cancellation performance with transmission delay difference in double tap in different signal bandwidth

4 结 语

本文提出了定向天线和全向天线的接收结构，通过干扰抵消算法，利用全向天线接收的非合作信号通过调整幅度和相位来抵消定向天线接收的非合作信号，从而保证合作信号的准确接收。提出了单抽头和多抽头2种结构模型，分别以最小剩余非合作信号功率为准则，进行了推导与仿真，对于单抽头结构通过延迟线和衰减器来调整信号的相位和幅度，干扰抑制能力随着带宽的增大而减小，载波中心频率处的干扰抑制效果最好，带宽边缘的频率分量干扰抑制效果最差；对于多抽头结构通过矢量调制器来调整信号相位及幅度，其最佳的干扰抑制效果与干扰信号带宽、抽头时延与干扰传输时延之差有关。本文的仿真结果得出的结论为后续硬件实现提供了理论支持和性能的评估。

/References:

[1] 赵红梅,王胜平. 扩频通信系统的抗干扰特性分析[J]. 河北科技大学学报,2011,32(6):1-4. ZHAO Hongmei, WANG Shengping. Analysis of inteference characteristics in spread spectrum communication system[J].Journal of Hebei University of Science and Technology,2011,32(6):1-4.

[2] 张海旭,贾翠霞,陈浩. 大功率认知干扰系统研究[J]. 河北科技大学学报,2011,32(6):139-144. ZHANG Haixu, JIA Cuixia, CHEN Hao. Research on high power cognitive interference system[J]. Journal of Hebei University of Science and Technology,2011,32(6):139-144.

[3] WIDROW B,GLOVER J R,MCCOOL J M. Adaptive noise cancelling: Principles and applications[J].Proceedings of the IEEE,1975,63(12):1692-1716.

[4] HUUSARI T,CHOI Y S,LIIKKANEN P,et al.Widebandself-adaptive RF cancellation circuit for full-duplex radio:Operating principle and measurements[C]//2015 IEEE 81st Vehicular Technology Conference (VTC Spring). Glasgow:[s.n.],2015: 1-7.

[5] CHOI Y S, SHIRANI-MEHRH. Simultaneoustransmissionandreception: Algorithm, design and system levelperformance[J]. IEEETransactions on Wireless Communications,2013,12(12):5992-6010.

[6] GLOVER J R. Adaptive noise canceling applied to sinusoidal interferences[J].IEEE Transactions on Acoustics, Speech, and Signal Processing,1977, 25(6):484-491.

[7] 杜武林.干扰抵消技术的原理和应用[J].电信科学,1988,30(5):51-55. DU Wulin. Principle and application of interference cancellation technology[J].Telecommunications Science,1988,30(5):51-55.

[8] 郑伟强,杜武林.自适应干扰抵消研究[J].电讯技术,1991,31(6):20-27. ZHENG Weiqiang, DU Wulin. Research on adaptive interference cancellation technique[J]. Telecommunication Engineering,1991,31(6):20-27.

[9] RINCON R, HILDEBRAND P, HILLIARD L, et al. Real-time beamforming synthetic aperture radar[J]. Proc of SPIE,2006,42:25-31.

[10]KRIEGER G, GEBERT N, MOREIRA A. Digital beamforming techniques for spacebornc radar remote sening[J].Proc of EUSAR 2006, Dresden, Gremany:2006,15:1-4.

[11]张德平. 数字阵列天线发射数字波束扫描技术研究[D].长沙:国防科学技术大学,2012. ZHANG Deping. The Study of Digital Array Antenna Transmitting Digital Beam Sweeping Technology[D]. Changsha: University of Defense Technology,2012.

[12]尹展,孙晨华.多波束卫星移动通信系统的同频干扰研究[J].无线电通信技术,2016,42(2):23-26. YIN Zhan, SUN Chenhua. Research on co-frequency interference in multi-beam satellite mobile communication system[J].Radio Communications Technology,2016,42(2):23-26.

[13]王和,刘光斌,程俊仁,等.卫星导航接收机抗干扰测试评估方法研究[J].无线电工程,2014,44(3):5-7. WANG He, LIU Guangbin, CHENG Junren, et al. Research on anti-jamming test evaluation method for satellite navigation receiver[J]. Radio Engineering,2014,44(3):5-7.

[14]于莹莹. 空时联合自适应天线抗干扰的研究[D]. 哈尔滨:哈尔滨工程大学,2013. YU Yingying. Research on Joint Space-time Adaptive Antenna Anti-jamming[D].Harbin: Harbin Engineering University,2013.

[15]谈江梅. 雷达干扰系统仿真研究[D]. 成都: 电子科技大学,2005. TAN Jiangmei. Simulation of Radar Jamming System[D]. Chengdu: University of Electronic Science and Technology of China,2005.

[16]王俊,赵宏志,卿朝进，等.同时同频全双工场景中的射频域自适应干扰抵消[J].电子与信息学报,2014,36(6):1435-1440. WANG Jun, ZHAO Hongzhi, QING Chaojin, et al.Adaptive self-interference cancellation at RF domain in co-frequency co-time full duplex systems [J]. Journal of Electronics and Information,2014,36(6):1435-1440.

[17]王俊,赵宏志,马万治,等.同时同频全双工宽带射频自干扰抵消性能分析[J].通信学报,2016,37(9):121-130. WANG Jun, ZHAO Hongzhi, MA Wanzhi,et al. Performance analysis of broadband self-interference cancellationat RF domain in co-frequency co-time full duplex systems[J].Communication Journal,2016,37(9):121-130.

[18]LU H T, SHAO S H, DENG K, et al. Self-mixed self-interference cancellers for full-duplex wireless communications[J]. Science China,2015,58(1):205-210.

[19]徐强,潘文生,全欣,等.同时同频全双工LTE射频自干扰抑制能力分析及实验验证[J].电子与信息学报,2014,36(3):662-668. XU Qiang, PAN Wensheng, QUAN Xin, et al.Analysis and experimental verification of RF self-interference cancelation for co-time co-frequency full-duplex LTE[J]. Journal of Electronics and Information,2014,36(3):662-668.

[20]刘亮,何攀峰,台鑫. 矢量调制在相干多通道信号发生中的应用研究[J]. 国外电子测量技术,2015,34(11):48-52. LIU Liang, HE Panfeng, TAI Xin. Research of application for vector modulation in the phase-coherent multichannel signal generation[J]. Foreign Electronic Measurement Technology,2015,34(11):48-52.

[21]方鑫. 高精度数字矢量调制器的研制[D]. 成都: 电子科技大学,2016. FANG Xin. Development of High Precision Digital Vector Modulator[D]. Chengdu: University of Electronic Science and Technology of China,2016.

[22]唐友喜.同时同频全双工原理与应用[M].北京:科学出版社,2016.

[23]文光俊,谢甫珍,李建.无线通信射频电路技术与设计[M].北京:电子工业出版社,2010.

Performance analysis of non-cooperation signal interference cancellation at RF domain

WANG Tianyu， SUN Zhigang， ZHENG Shumei

(The 54thResearch Institute of CETC, Shijiazhuang, Hebei 050081, China)

Due to the lack of effective methods for broadband interference suppression in aerospace TT&C system, the receiving structure of the directional antenna and the omni-directional antenna is provided. Non-cooperative signal is cancelled at RF domain, so as to ensure the accurate reception of the cooperative signal. Two syntactic models of the single tap and the multi-tap are discussed separately. Theoretical derivation is proceeded with minimizing the residual non-cooperative signal power as criterion by using the interference cancellation algorithm. It is suggested that the vector modulator be used to adjust the amplitude and phase in the multi-tap structure. The simulation result shows that, for the single tap structure, when the delay line error is 2%, the best interference cancellation capability reaches 45 dB in the 2.6 GHz band, for the bandwidth 100 MHz siganl; while when amplitude error is 10%, the interference cancellation capability decreases by 10 dB; for the multi-tap structure, the same signal is used as the single tap structure. In the double tap structure, the best interference cancellation capability reaches 81 dB when the transmission delay is confirmed. The simulation results verify the feasibility of the receiver structure.

wireless communication technology; RF adaptive interference cancellation; single tap; multi-tap; vector modulator; delay line

1008-1534(2017)04-0247-07

2017-04-29;

2017-06-06；责任编辑：李 穆

王天宇(1993—)，男，河北石家庄人，硕士研究生，主要从事无人机测控方面的研究。

孙志刚研究员。E-mail:zhigsun@sina.com

TN973.3

A

10.7535/hbgykj.2017yx04003

王天宇，孙志刚,郑淑梅.非合作信号射频域干扰抵消性能分析[J].河北工业科技,2017,34(4):247-253. WANG Tianyu， SUN Zhigang，ZHENG Shumei.Performance analysis of non-cooperation signal interference cancellation at RF domain[J].Hebei Journal of Industrial Science and Technology,2017,34(4):247-253.