基于遗传算法的汽车仪表板横梁参数优化

周 磊 孟正华 许 欢 郭 旋

1(武汉理工大学汽车工程学院 湖北 武汉 430070)2(上汽通用五菱汽车股份有限公司 广西 柳州 545007)

基于遗传算法的汽车仪表板横梁参数优化

周 磊1,2孟正华1许 欢1郭 旋1

1(武汉理工大学汽车工程学院 湖北 武汉 430070)2(上汽通用五菱汽车股份有限公司 广西 柳州 545007)

节能、安全和环保是汽车工业的发展方向，汽车轻量化是实现节能减排的重要手段，以重量为目标的汽车零部件结构优化设计对减轻零件重量、提升整车性能具有重要的工程意义。以上汽通用五菱股份有限公司某车型仪表板横梁总成结构为研究对象，利用有限元分析方法对汽车仪表板横梁进行性能分析，通过正交试验方法找出对汽车仪表板横梁重量和振动性能影响较大的因素，并利用遗传算法进行结构参数优化。结果表明，在不影响各项性能的前提下，通过优化设计方法，该仪表板横梁总成减重9.96%，取得了较好的轻量化效果。

汽车轻量化 仪表板横梁 正交试验 遗传算法 优化设计

0 引 言

仪表板横梁CCB(Cross Car Beam)是汽车仪表板系统的支撑结构件。典型的仪表板横梁主要包括：主横梁，吸能支架，安装转向管柱、乘员安全气囊、线束、倒车雷达、空调等部件的支架。CCB作为仪表板系统的主要支撑受力零件，其性能直接影响了汽车的安全性和舒适性，如方向盘的怠速抖动和汽车匀速行驶时仪表板总成内部的振动异响等[1-5]。同时，随着汽车轻量化要求的不断提高，车身系统子零件的轻量化设计也相应受到重视；CCB在仪表板系统中重量占比较大，其轻量化设计正逐步受到关注。蔡庆荣等[2]基于Isight对汽车仪表板横梁的直径和壁厚等关键设计变量进行优化设计，提高结构利用效率，达到性能优化目的。庞志远等[3]基于TRIZ理论对横梁刚度进行分析并对结构进行优化，得到了高固有频率、高结构强度并且质量小的结构。宣海军等[4]提出了一种改善CCB系统固有振动特性的思路，利用LMS Test.Lab测试系统对系统进行约束模态试验，找到固有振动特性较差的原因，并对对系统进行优化。Chao Li等[5]对汽车仪表板横梁的拓扑结构、尺寸及形状进行优化，并对采用不同工艺制作的管梁进行性能及成本分析，得到成本低、性能优的横梁结构。总体而言，大部分研究学者对CCB整体结构进行了优化设计，并取得了相应成果。本文以上汽通用五菱股份有限公司某车型CCB为研究对象，基于Optistruct软件进行模态、刚度分析，分析其振动性能，并通过正交试验全面分析管梁厚度、外径与各支架结构尺寸等子零件结构参数对CCB振动性能的影响规律。根据正交试验结果，以横梁的几个结构参数为设计变量，总成质量最小为目标，满足振动性能为约束条件，运用响应曲面法建立多变量和优化目标之间的多元线性回归模型，并采用遗传算法进行参数优化，实现轻量化的目的。

1 性能分析

1.1 有限元模型的建立

本文以上汽通用五菱股份有限公司某车型CCB为研究对象，在Hypermesh中建立有限元模型。该模型主要采用精度较高的四边形板壳单元，部分位置采用三角形单元，支架和管梁之间采用刚性单元RBE2模拟结构间实际连接，车身固定点位置采用6自由度约束，而对于空调、安全气囊、线束总成等附件采用质量块的形式模拟实际安装状态加载在质心处[6]。CCB各结构材料均采用低碳钢，材料属性见表1所示。建立的有限元模型如图1所示，单元个数86 727个，节点个数89 500个。

表1 材料属性

图1 CCB的有限元模型

1.2 仪表板横梁性能分析

CCB作为仪表板系统的主要支撑受力零件，其模态、刚度和强度直接影响了汽车的安全性和舒适性，通常情况下，汽车发动机的怠速频率为25～28 Hz，方向盘与转向管柱的一阶固有频率为50 Hz以上，通过大量工程实践检验，仪表板的一阶固有频率33～35 Hz。为了避免仪表板横梁与发动机发生共振，通常要求横梁总成约束状态下的一阶固有频率大于35 Hz[4,7]。同时，根据企业相关规定，在2倍重力加速度载荷下，CCB的最大变形位移应小于2 mm，最大应力应小于210 MPa。

采用Hypermesh中的OPTISTRUCT求解器来计算CCB的约束-自由模态。考虑到模态截断问题，计算模型的10阶模态，以保证前5阶模态的准确性，前五阶模态计算结果如表2所示。采用Hypermesh中的RADIOSS求解器对CCB进行强度分析，计算结果如表3所示。由计算结果可知，CCB的一阶模态频率为39.19 Hz，高于标准规定的35 Hz，各零部件不会与车身各大总成产生共振，都满足整车性能要求；最大变形位移为0.23 mm，远小于2 mm；最大应力96.68 MPa，远小于210 MPa。因此，各项参数均满足相关要求，且具有较大的优化空间。

表2 前五阶固有频率及振型

表3 强度分析结果

2 横梁总成灵敏度分析

通过对横梁支架自身的模态要求、横梁支架结构设计以及相关的车身结构设计等进行研究，找出对横梁结构自身重量影响不大，而对模态性能影响较明显的结构参数，进行结构改进和优化，以期得到既能满足振动性能要求，且质量较小的横梁总成设计方案。

灵敏度分析是结构优化设计中重要的一环，可显著提高优化效率。这一过程通常可以算出结构响应值对于设计变量的导数，以确定设计变化过程中对结构响应最敏感的部分，从而可以获得最关心的灵敏度系数和最佳的设计参数[8]。由于整个CCB的结构参数较多，如果将所有的结构参数都提取出来作为控制变量，收集数据的工作量以及后期的计算量十分庞大。通过查阅相关论文文献和资料，只提取一些对振动性能可能影响较大的结构参数进行灵敏度分析，选择影响程度较高的因素进行参数优化。根据实际设计经验并参考相关文献，最终选取如图2中所示的10个结构参数作为研究对象进行模拟试验。图2中各参数的含义和变量水平见表4所示，表中水平变化值表示每个水平变量相对于前一水平值的变化量。

图2 选定控制因子对应的结构设计参数示意图

表4 控制因子变量水平

正交试验以横梁支架重量和一阶振动频率为试验指标。根据所选因素和变量水平，试验选择十因素三水平，考察各因素对横梁支架重量和一阶频率的影响，不考虑因素之间的相互作用，采用L27(311)正交表(取前10列)。利用OPTISTRUCT求解器进行仿真分析得到一阶固有频率P和总质量M，并通过分析田口设计得出各参数的灵敏度，如表5所示。

表5 强度分析结果

由表5可知，对横梁支架总成的一阶固有频率(P)影响最大的是管梁结构的厚度(K)，其次是前上结构与车身连接点位置(C)，再次是管梁外径(J)、H型支架厚度(H)和前上结构的厚度(D)，其他因素的影响则很小；而对横梁支架总成质量(M)影响最大的是管梁结构的厚度(K)，其次是管梁外径(J)、H型支架厚度(H)和前上结构的厚度(D)。综合各因素对一阶固有频率及总质量的影响程度，并考虑各附件的装配要求及标准化要求，在保持J(管梁外径)不变的条件下，选取K(管梁厚度)、C(前上结构与车身连接点位置)、H(H型支架厚度)和D(前上结构厚度)作为后续优化过程的结构参数自变量。

3 结构参数优化

基于正交试验结果，以横梁总成质量最小为优化目标，在满足NVH性能等约束条件下，利用响应曲面法建立多变量和优化目标之间的多元线性回归模型来代替有限元模型，并使用遗传算法进行结构参数的优化，达到汽车轻量化的目的。

3.1 数学模型的建立

车身前围板和横梁总成主要部件都是由钣金制成，在不改变前围板的拓扑形式、横梁总成整体尺寸和约束方式的前提下，基于正交试验的结果分析得出的横梁支架结构参数对其振动性能的影响规律，选取管梁厚度(K)、前上结构与车身连接点位置(C)、H型支架厚度(H)和前上结构的厚度(D)这几个结构设计参数作为设计变量x1、x2、x3、x4，在满足横梁总成NVH性能等约束条件下，使得横梁总成重量m(x)最小，则横梁总成的优化数学模型为：

设计变量：X=[X1,X2,X3,X4]

目标函数：minM(X)=f(X1,X2,X3,X4)

式中：X为选取的优化变量，M(X)为横梁总成重量，F(X)是横梁总成一阶固有振动频率。

为了准确地表达各变量与优化目标及约束条件间的关系，在正交试验的基础上，采用响应曲面法RSM(Response Surface Methodology)建立多变量和优化目标之间的多元线性回归模型，并在所建模型上进行剩余优化工作。响应曲面方法是指利用多项式函数拟合设计空间的方法，计算简单，且具有良好的鲁棒性[9]。

响应曲面法中最常用的是利用中心复合试验设计(CCD)在获得一定量的实验数据来拟合合适的数学模型。具体试验中，在上述正交试验基础上，保持其他参数不变，利用Minitab软件中的创建响应曲面设计模块进行中心复合试验设计。设计因子水平如表6所示，并利用OPTISTRUCT求解器进行仿真分析得到各组试验结果。

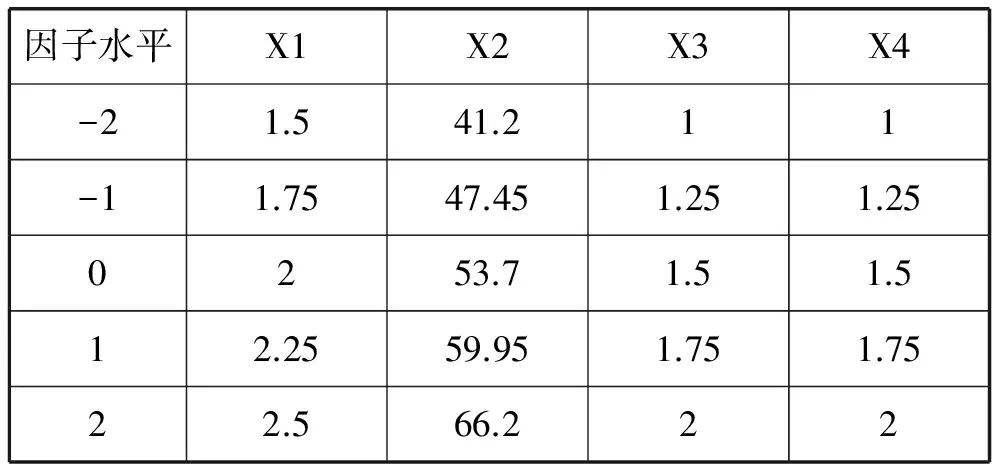
表6 中心复合设计因子及其水平值

利用Minitab软件中的分析响应曲面设计模块进行响应面模型的拟合，得到如式(1)、式(2)所示的数学模型。F(X) =-2.57+0.190 1×X1+0.63×X2+2.16×X3+

24.84×X3-0.002 062×X1×X1-0.879×X2×X2-

0.487×X3×X3-3.879×X4×X4+

0.052 4×X1×X2+0.007 8×X1×X3-

0.048 4×X1×X4- 0.511×X2×X3+

0.424×X2×X4+0.133×X3×X4

(1)

M(X) =3.45+0.002 2×X1+0.035×X2+0.048×X3+

1.733×X4-0.000 070×X1×X1-

0.032 6×X2×X2-0.034 6×X3×X3-

0.068 6×X4×X4+0.006 50×X1×X2+

0.006 50×X1×X3-0.006 50×X1×X4-

0.183×X2×X3+0.187×X2×X4+

0.183×X3×X4

(2)

为确保所得模型的准确性，对模型进行精度分析。表7中R-sq代表拟合的总效果多元全相关系数，而R-sq(调整)代表修正的多元相关系数，R-sq越大且两者越接近代表拟合的效果越好。从表中可看出，R-sq和R-sq(预测)的值很接近，且R-sq的值分别为99.89%和99.71%，说明采用式(1)和式(2)来描述因子与一阶固有频率f(x)和质量m(x)之间的关系是准确的、可行的[9-10]。

表7 响应曲面模型检验结果

3.2 基于遗传算法的结构参数优化

遗传算法是由美国的J.Holland教授于1975年最先提出的一种模拟达尔文生物进化论中自然选择和群体遗传机理的随机优化算法。与传统的优化算法相比，由于具有内在的隐并行性和更好的全局寻优能力，遗传算法更加适用于复杂形态函数的全局寻优，而且由于搜索的本质并行性，工作效率更高[11]。

设计遗传算法的基本过程可大致分为制订编码方案、确定适应值函数、确定选择策略、设计交叉和变异操作、选取控制参数等几个步骤，图3显示了遗传算法优化流程[12-13]。

图3 遗传算法优化流程

根据遗传算法的设计流程，在Matalab软件中编写实现遗传算法的程序包，针对目标函数最小值求解问题，遗传算法优化的各参数设定如下：初始种群规模为40，进化代数150，全局杂交和变异概率分别为0.7和0.01[13]。图4为各变量和目标函数值在遗传算法优化迭代过程中的变化情况。由图4可知，随着迭代的进行，各变量数值整体呈下降趋势，并最终保持水平状态。由于遗传算法存在基于自然选择和群体遗传机理的特性，并且在遗传过程中伴随着复制、交叉和变异的发生，因此存在参数上下波动的情况，但随着物种的进化，种群对环境的适应度不断提高，最终各变量会达到稳定状态，即各变量达到最优[11]。经过迭代计算后，质量的最小值为6.96 kg，对应的参数：前上结构与车身连接点位置为43.0 mm，前上结构厚度为1.0 mm，H型支架厚度为1.0 mm，管梁厚度为1.83 mm。

将优化后的模型进行CAE仿真分析，与3.2节中的性能分析结果进行比较，优化前后的性能状态对比见表8所示。可以看出，经过参数优化，总质量降为6.89 kg，与经过迭代计算得到的数据基本一致，也可以得出相应曲面相应模型是可靠的。因此，在保证各项性能满足振动性能的情况下，经过参数优化，横梁总质量减轻0.69 kg，减重比例达9.10%。

根据优化分析结果，将优化后的横梁总成结构进行重新建模，如图5所示。上汽通用五菱股份有限公司根据模型设计并生产了如图6所示的仪表板横梁总成，测得仪表板横梁总成实重7.05 kg，相比于优化前的实重7.83 kg，减重达9.96%。优化后的仪表板横梁总成广泛运用于上汽通用五菱股份有限公司的现生产车型，根据实车测试，各零部件不会与车身各大总成产生共振，满足整车性能要求。

图5 优化后的数模图

图6 优化后的实物图

4 结 语

(1) 利用正交试验方法对汽车仪表板横梁各结构参数进行全面分析，找出了对汽车仪表板横梁一阶固有频率和质量影响较大的因素有K(管梁厚度)、C(前上结构与车身连接点位置)、H(H型支架厚度)和D(前上结构厚度)，为汽车仪表板横梁的设计提供了参考依据。

(2) 使用基于响应曲面法建立的近似模型进行参数优化，计算简单，提高了计算效率，系统性、实用性强。

(3) 利用遗传算法根据相关标准要求对汽车仪表板横梁进行参数优化，在保证满足各项性能要求的前提下，横梁总成实量减少0.78 kg，减重比例达9.96%，实现了汽车轻量化的目的。

[1] 曹渡.汽车内外饰设计与实战[M].北京：机械工业出版社，2011：167-212.

[2] 蔡庆荣, 董丹丹, 夏建新,等.基于Isight 的仪表板横梁优化[J].计算机辅助工程，2013，22(S2)：221-225.

[3] 庞志远，梁鹏，田佳平.基于TRIZ理论的仪表板横梁优化设计[J].机械研究与应用，2009，22(4)：99-101.

[4] 宣海军，苏荣，江腾飞.汽车仪表板横梁系统固有振动特性研究[J].机械设计与研究，2014，41(4)：37-41.

[5] Li C, Kim I Y. Topology, Size and Shape Optimization of an Automotive Cross Car Beam[C]//Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering, 2015.

[6] 刘伟萍.仪表板性能分析及优化[D].武汉:武汉理工大学，2010：10-25.

[7] 田佳平，迟秀颖.仪表板横梁结构灵敏度与横梁的振动特性分析[C]//2013中国汽车工程学会年会论文集. 北京：机械工业出版社，2013：1646-1649.

[8] 曹文钢，曲令晋，白迎春.基于灵敏度分析的客车车身质量优化研究[J].汽车工程，2009，31(3)：278-281.

[9] 傅厦龙，胡夏夏.基于响应曲面和遗传算法的工艺参数优化[J].高分子材料科学与工程，2014(04)：123-126.

[10] 郎利辉, 杨希英, 孙志莹,等. 基于响应面法的汽车覆盖件充液成形工艺参数多目标优化[J].汽车工程, 2015,37(4):480-484.

[11] 郭巍.微型汽车内外饰产品设计制造技术基础研究[D].武汉:武汉理工大学，2013：139-140.

[12] Fang Lincun, Qin Shiyin, Xu Gang, et al. Simultaneous optimization for hybrid electric vehicle parameters based on multi-objective genetic algorithms[J].Energies,2011,4(3):532-544.

[13] 史峰, 王辉, 郁磊. MATLAB智能算法30个案例分析[M].北京：北京航空航天大学出版社，2011:20-24.

PARAMETERS OPTIMIZATION OF CROSS CAR BEAM BASED ON GENETIC ALGORITHM

Zhou Lei1,2Meng Zhenghua1Xu Huan1Guo Xuan1

1(SchoolofAutomotiveEngineering，WuhanUniversityofTechnology,Wuhan430070,Hubei,China)2(SAICGMWulingAutomobileCo.,Ltd,Liuzhou545007,Guangxi,China)

Energy saving, safety and environmental protection are the development directions of the automobile industry, and the automotive lightweight is an important technology to realize energy saving and emission reduction. The structure optimization design of automotive components aimed at weight has an important engineering significance for reducing part weight and improving vehicle performance. Taking a certain type of fascia board beam structure of SAIC GM Wuling Automobile Co., Ltd as the research object in this paper, the performances of fascia board beam were analyzed with the finite element analysis method and the influential factors for mass and vibration performance were investigated with the orthogonal experiments, then the structural parameters were also optimized by genetic algorithm. The results indicate that the weight of the fascia board beam reduces by 9.96% without performances loss with the parameter optimization method in this paper.

Automotive lightweight Cross car beam Orthogonal experiment Genetic algorithm Optimization design

2016-08-16。湖北省自然科学基金(2014CFB176)；武汉市科技计划项目(2013011803010606-4)。周磊，硕士生，主研领域：汽车内外饰设计。孟正华，副教授。许欢，硕士生。郭旋，硕士生。

TP3

A

10.3969/j.issn.1000-386x.2017.06.015