几何估算和RSSI相结合的室内定位算法

徐 驰 邱 添 曹广成

1(上海应用技术大学 上海 201418)2(上海京颐科技股份有限公司 上海 200240)

几何估算和RSSI相结合的室内定位算法

徐 驰1邱 添2曹广成1

1(上海应用技术大学 上海 201418)2(上海京颐科技股份有限公司 上海 200240)

提出一种基于几何估算和RSSI相结合的定位方法。方法中，未知节点的位置可以通过参考节点的通信范围进行几何估算。参考节点的通信重叠区域可以估算出未知节点位置。在几何估算方法的基础上又引入了RSSI值优化。利用RSSI值对几何估算区域进行划分，运用改进公式计算出新的未知节点位置。实验结果表明，该方案优于基础定位算法，拥有较高的精度。同时在医院场景进行了初步系统测试，获得了良好的定位效果。

几何估算 接收信号强度 室内定位

0 引 言

近年来，硬件技术的发展促使微型化传感器设备通信能力的提升。无线传感网络是由大量的无线传感器对空间进行数据检测、信息收集。因此，无线传感网可以进行实时数据采集、分析、监控和即时响应时间。由于上述优势，无线传感网成为了目前一个非常活跃的研究课题，在诸如医疗、工业、楼宇自动化、环境监测和商品位置跟踪等领域广泛运用。节点定位是无线传感网络中最重要的问题之一。因为位置信息在许多基于位置的服务和应用中扮演重要的角色。例如，当火灾或者抢劫事件发生在无线传感器网络环境中，为了处理此事件，可能需要知道处理此事件传感器节点的位置。GPS是非常有用的定位技术。但是在很多情况下，由于节点的便捷性与能耗无法用GPS和其他定位仪器满足所有情况。因此，如何在不使用GPS技术的情况下解决传感器位置问题变得非常重要。

为了有效解决室内定位这一难题，各种新型室内定位技术层出不穷。如蓝牙定位技术(谷歌方案)、红外定位技术[1]、地磁定位技术[2](IndoorAtlas方案)、UWB定位技术[3]、3G/4G信号定位技术[4](Qubulus方案)、WiFi定位技术[5]、LiFi定位技术[6]、WiMax定位技术[7]、ZigBee定位技术[8]等。其中蓝牙[9]、WiFi、ZigBee[10]等技术应用最为广泛，地磁、LiFi等技术是异军突起的新技术。为了降低硬件成本，进而提出了基于非测距的定位。其无需专用测距、测角度的硬件设施与基于测距的定位相比成本更低、复杂度更小。但是目前大多数的基于非测距的定位仍然成本高且定位精度偏低。

本文提出了一种基于几何估算和RSSI相结合的定位算法，利用参考节点几何估算方案[11]的几何测算，RSSI值方案的距离计算，综合考量环境等多种因素，从而实现高精度的室内定位系统。需要事先设定参考节点与未知节点的参数信息，同时算法只需知道各节点之间RSSI大小的关系，而并不关心RSSI值具体的数值，所以所付出的硬件代价较小。下面将对算法进行详细的介绍。

1 相关工作

室内定位技术很多，根据其定位采用的方案可以分为两种：基于测距和基于非测距的定位技术。基于测距的方案需要计算得到两个通信节点之间的距离信息或者角度信息，通过得到的位置信息计算未知节点的坐标[12]。基于非测距的方案则利用节点和网络的自身属性对未知节点的位置进行估算[13]。

1.1 基于测距定位方案

基于测距定位利用节点间的距离或角度信息来计算位置节点位置。典型的方案如到达时间(TOA[14])、到达时差(TDOA)[15]、到达角度(AOA)和接收信号强度(RSSI)[16]。TOA通常是测量范围内两个通信节点之间信号传播时间。一般使用超声波此类低速信号。TDOA与TOA非常相似，它利用不同速度的两个信号到达时间差来计算距离。AOA是通过估计相邻节点之间的相对角度。其最初被广泛应用于蜂窝网络，要求每个接收器都必须具备额外的天线才能检测到发射器的信号。RSSI是目前最广泛、最低廉的距离测量方案。接收机接收信号的RSSI值后通过信号传播衰减模型计算出距离。但是，在实际环境中由于许多不可预测的因素，如噪声、信号干扰、多径传播延迟等，使用RSSI进行距离估计往往是不准确的。上述基于测距定位方案需要一些额外的昂贵、复杂的硬件设施，因此这样的定位方案不适合网络资源有限的无线传感器网络。

1.2 基于非测距定位方案

基于非测距定位方案不需要任何时间、角度、信号强度等数据。文献[17]通过邻居节点的位置信息并利用质心公式来估计未知节点的位置。其主要依靠邻居节点的数量来提升定位精度，在邻居节点数量少时精度很低。这类利用通信重叠区域的非测距定位方案被称为几何估算方法。DV-Hop的定位方案[18]是利用无线网络自身的属性来测定距离，其核心思想是用网络数据每跳的距离和参考节点到未知节点跳数的乘积，表示参考节点到未知节点的距离。未知节点的位置计算依靠参考节点的位置、跳数、每一跳平均距离等参数。APIT算法[19]核心思想是未知节点从它所有通信的参考节点中选择三个参考节点，计算它是处于这三个参考节点组成的三角形内部还是外部，然后再选择其他三个参考节点进行同样的计算，直到计算完所有的三角形组合或者达到设定的阈值，最后未知节点将包含其所有的三角形的相交区域的质心作为自己的估计位置。

2 定位算法

2.1 几何估计算法

几何估算方法其主要是利用参考节点与未知节点之间所处于的几何位置关系对未知节点位置进行估算。其几何描述如图1所示。本文排除了未知节点仅被一个参考节点所感知的情况，因为上文利用参考节点的位置摆放已经有效地预防了该极端情形。图1描述的是未知节点只被两个参考节点所感知，其中A1和A2为参考节点，圆形位置为未知节点M的实际位置，方形位置为未知节点M的估算位置。

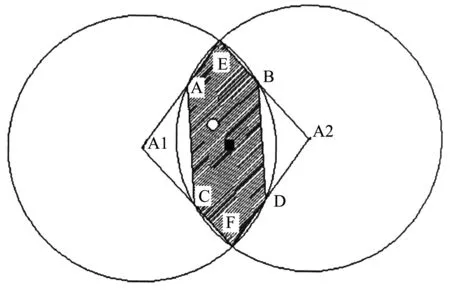
图1 未知节点被两个参考节点感知

其方法过程描述如下，首先参考节点必须具备相同的通信半径R，且不能移动。未知节点被两参考节点感知，说明其存在于两参考节点通信圆重叠部分。但重叠部分为凸型结构无法估算未知节点几何位置。两通信圆的交点分别为点E和点F。已知参考节点A1和A2的坐标分别为(x1,y1)和(x2,y2)，列方程求解得到E和F的坐标分别为(xe,ye)和(xf,yf)。计算公式(1)如下所示：

(1)

图形中点A、点B、点C和点D分别是直线A1E、A2E、A1F和A2F与两圆的交点，通过式(2)计算出点A的坐标，同理可以计算出点B、点C和点D的坐标。

(2)

通过联立直线和圆的方程能计算出两个A的坐标，去除在A1通信圆之外的坐标，剩余的则为A点的坐标。得到A-F点的坐标后构造出一个多边形，这个多边形的质心则为几何估计法的未知节点位置。未知节点的坐标如式(3)所示：

(3)

下面介绍另一种情况，未知节点被三个参考节点所感知。同时特例的情况是未知节点被多个参考节点所感知后，根据实现设置好的阈值选取最优的前三个参考节点进行定位计算。未知节点被三个参考节点定位的效果如图2所示。还有一种三个参考节点通信区域几乎重叠的文章并未给出，因为此种情况无法进行定位，且在参考节点位置布置阶段已经剔除此种可能。在理论模型当中，参考节点均匀分布，且重叠区域处于三个通信圆的中间位置。图2中圆形代表未知节点的实际位置，方形代表未知几点的估计位置。

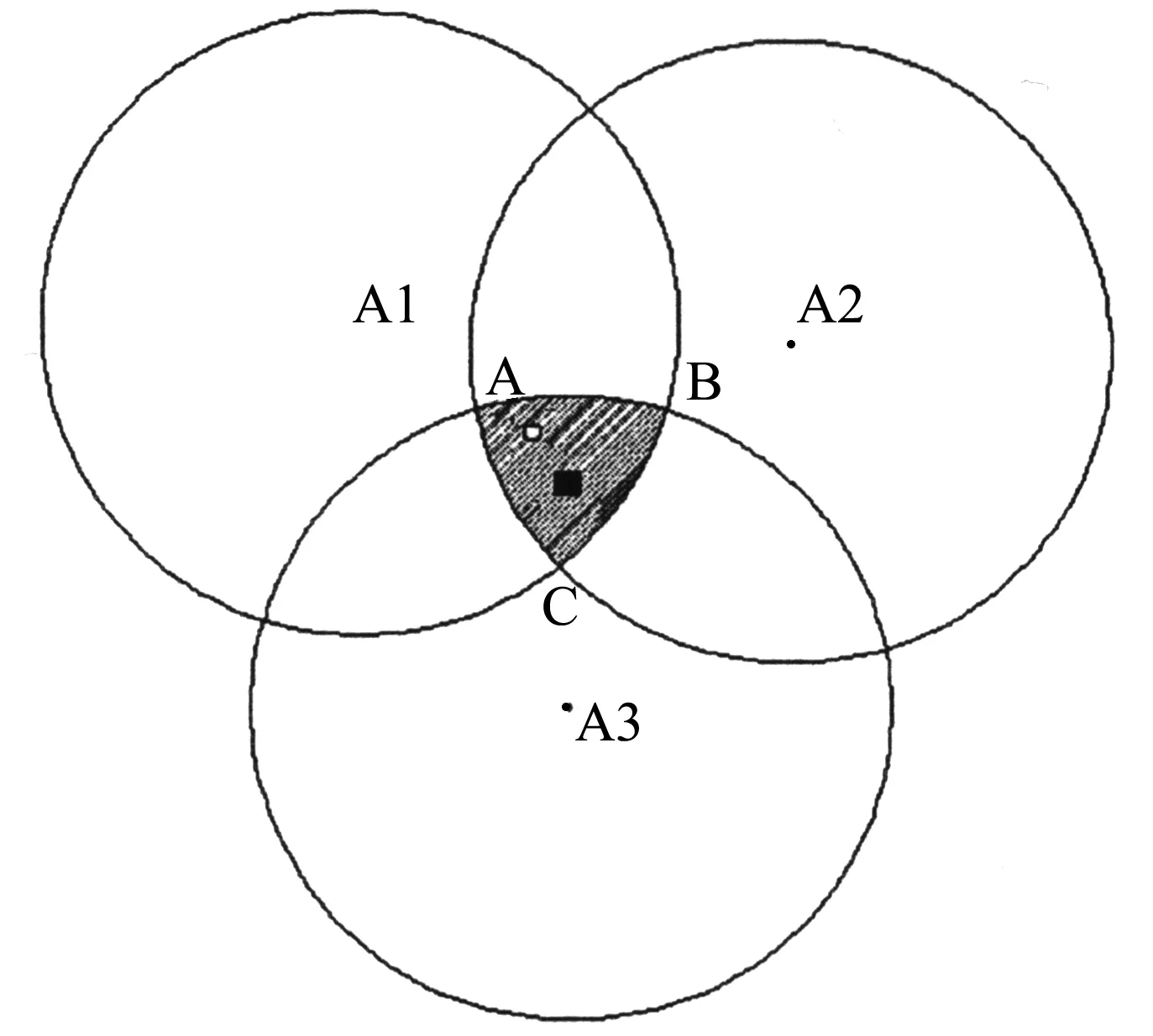
图2 未知节点被三个参考节点感知

已知参考节点A1、A2、A3的坐标分别为(x1,y1)、(x2,y2)、(x3,y3)，其通信圆两两之间的交点为A、B、C，坐标计算公式如下：

(4)

解方程可得A的坐标为(xa,ya)和(xa′,ya′)，滤除不在A1通信范围内的点，最终得到A的坐标为(xa,ya)。同理可以计算出B和C的坐标，分别为(xb,yb)和(xc,yc)。最终利用几何估算方法，未知节点M的坐标为(xm,ym)：

(5)

2.2 几何估算和RSSI值结合算法

2.2.1 前置条件

第一是网络中参考节点的功率必须相同。在几何估算方法中需要使用参考节点的通信半径进行换算，而通信半径与参考节点的功率之间有关系。前期需要实验室测量节点的通信半径。实验室测量的通信半径和理论通信半径误差在30 cm内为标准。参考节点的功率与参考节点的电源供给和天线功率正比关系。所以本文中所有参考节点电源全部采用220 V转5 V供电。使用PCB天线和2.4G无线技术。

第二是网络中参考节点的位置摆放。参考节点数量少于3个时，未知节点定位误差特别大或无法定位。参考节点摆放过密时，网络通信冗余，网络质量下降，网络定位的实时性下降。在定位系统实施需要进行参考节点位置摆放的设计与实施。保障整个网络中未知节点都能被三个以上的参考节点扫描。

第三是对RSSI值的修正。基于RSSI值定位算法在网络运行过程中每个节点对收集的RSSI值也需要进行修正，去除波动和奇异值点。文献[18，19]中利用卡尔曼滤波、最小均方差等方法对RSSI值进行处理。文章运用最简单的方法对RSSI值进行处理。每个节点收集3个RSSI值，然后利用均值法去除波动。

第四是对RSSI值的排序。RSSI值的排序分为两部分，一部分是未知节点的排序。未知节点在收到三个以上参考节点的信息后，针对RSSI值小的前三个参考节点进行组网通信。因为RSSI值越小说明参考节点与未知节点的距离越近，所以筛选出未知节点最近的前三个参考节点作为定位算法的前置条件。另一部分是上位机软件对参考节点接收到未知节点的RSSI值进行排序。该排序的作用是为了减少几何估算的区域，提高算法的精度。

2.2.2 算法模型

未知节点被两个参考节点所扫描。如图3所示是两个参考节点的模型。其中未知节点的实际位置为圆形点。方形点是几何估算方法的估算点。

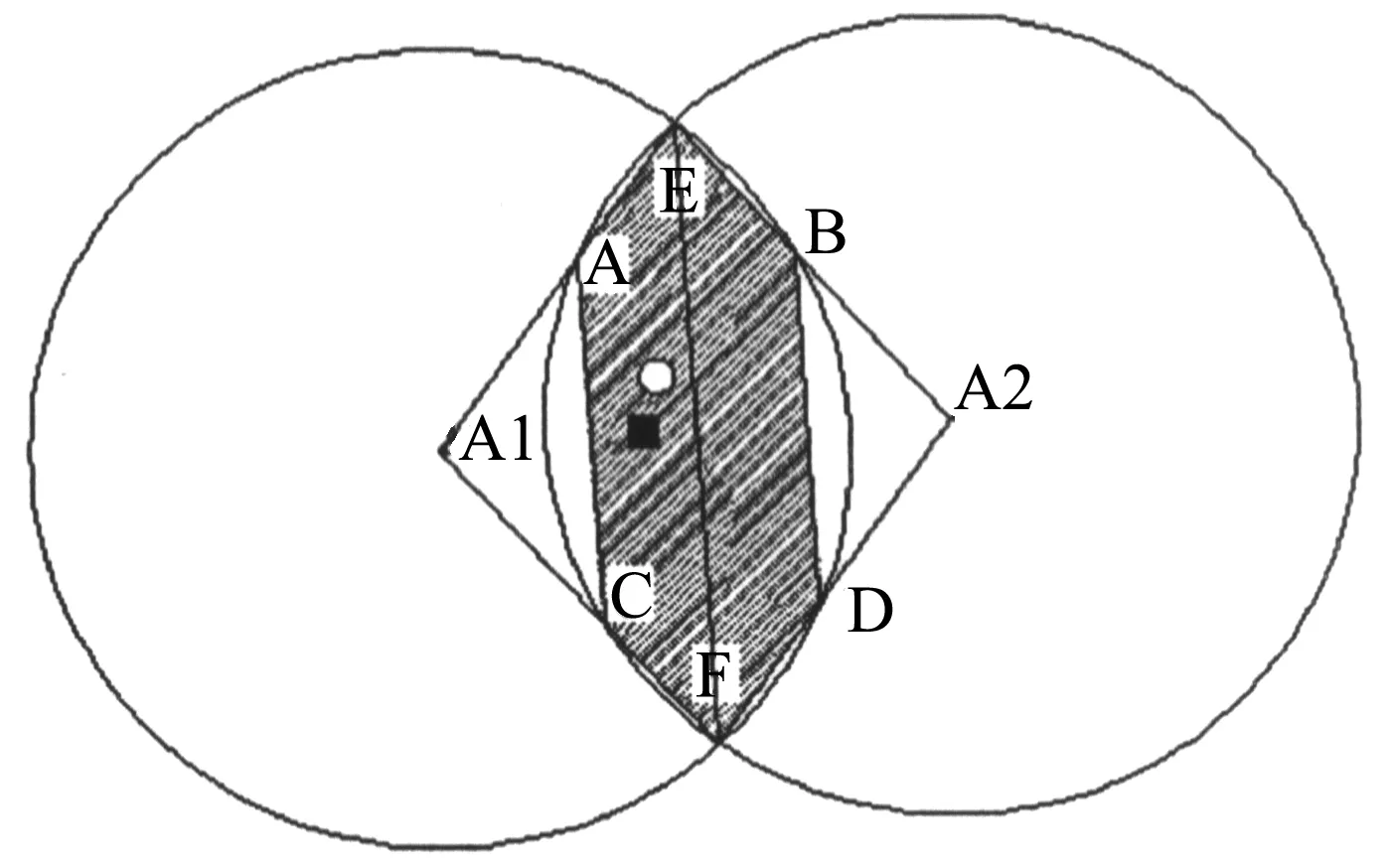
图3 两参考节点模型

根据未知节点与参考节点的实际位置可知RSSIA1>RSSIA2。实际位置中未知节点离参考节点A1更近。所以连接EF将多边形ABCDEF分为两个部分，而未知节点处于多边形AEFC的概率大于未知节点处于多边形EBDF的概率。所以几何估算只需要在左边图形当中进行，能够有效地减少定位误差。图中所示方形为优化后的估计位置，很明显误差减少了一半。改进后的未知节点M的坐标如式(6)所示：

(6)

如图4所示是三个参考节点的模型。其中圆形是未知节点的实际位置，方形是未知节点的估计位置。上位机收集了参考节点与未知节点的RSSI值，并对三个RSSI值进行排序。排序结果为RSSIA1>RSSIA3>RSSIA2。排序结果可知未知节点离参考节点A1最近，其次是参考节点A3，最后是参考节点A2。

图4 三参考节点模型

C、H是圆A1和圆A2的交点，A、G是圆A2和圆A3的交点，B、I是圆A3和圆A1的交点。连接CH、AG、BI将三圆重叠部分分割成6个区域。我们将其中的1、2区域划分到圆A1的范围内，3、4区域划分到圆A2的范围内，5、6区域划分到圆A3的范围内。根据上文当中的排序，未知节点最靠近参考节点A1，所以先把未知节点的区域划分到靠近参考节点A1的1、2区域。然后进行下一步判断，未知节点比较靠近参考节点A3，所以将未知节点的区域划分到靠近参考节点A3的1区域。所以未知节点最后的估算区域为1区域。1区域的质心坐标即为未知节点的估计坐标。

各点坐标计算过程如下：

A、G点的坐标计算如式(7)所示：

(7)

B、I点的坐标计算如式(8)所示：

(8)

O点的坐标计算如式(9)所示：

(9)

D点的坐标计算如式(10)所示：

(10)

最后通过质心算法求出未知节点的坐标。上述方法是将几何估算方法的估算区域缩小至之前的六分之一。在此基础上继续加入构造三角形优化进一步提高算法的精度。连接A1A2、A2A3、A3A1后形成构造三角形，将阴影部分缩小如图5所示，形成了新的阴影区域1、2、3、4、5、6。经过构造三角形优化过后的算法比优化之前的精度进一步提高。缩小了估算范围，最终利用质心法得出了未知节点的坐标。最终估算坐标与实际坐标非常接近，误差很小。

图5 构造三角形优化

3 仿真实验与实际检测

3.1 仿真实验与分析

利用Matlab仿真软件将本文算法与基于RSSI值方法、几何估算方法进行对比。分别就定位算法的精度和稳定性做了详细的仿真测试，下面分别介绍仿真测试的结果。

设置参考节点的通信半径为10 m，参考节点数量50个，未知节点数量50个随机分布在网络当中。定位范围为50 m×50 m的正方形区域。图中“+”表示未知节点的实际位置，“*”表示未知节点的估计位置。图6是RSSI方法的仿真结果。图7是几何方法的仿真结果。图8是本文方法的仿真结果。RSSI方法定位精度的波动很大，在某些区域内参考节点分布密集，定位效果好，某些区域内参考节点分布稀疏，定位效果差。几何方法定位的精度普遍偏低，在整个覆盖范围内定位误差较大，但受参考节点分布影响较小，比较稳定。本文算法效果较好，定位精度和稳定性较之RSSI方法和几何方法都有提升。保留了RSSI方法的定位精度，几何方法的稳定性。

图6 RSSI方法仿真结果

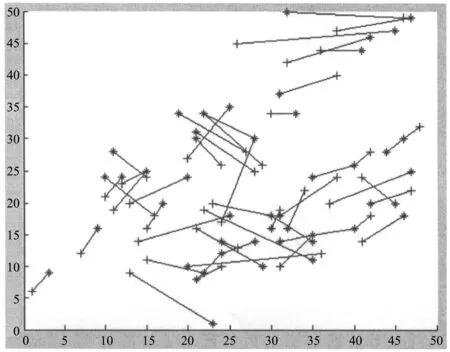
图7 几何方法仿真结果

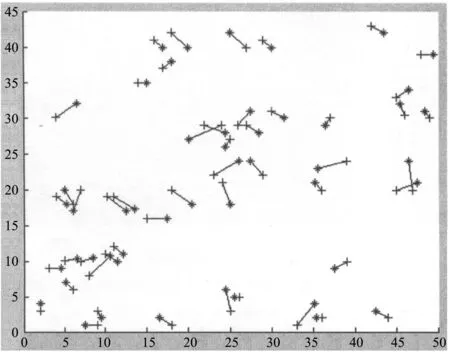
图8 本文方法仿真结果

选取10～100个参考节点，10～100个未知节点，通信半径为5 m，在50 m×50 m的方形范围内进行定位测试。设置实际位置与估计未知距离在2 m内的为定位成功。图9中是仿真结果，横坐标为节点数量，纵坐标为定位成功率。RSSI方法随着节点数量的增加定位效果产生波动，但整体维持在80%水平。几何方法定位精度随着节点的增加而提高。节点数量为10个是定位精度只有30%。随着节点的数量增加，几何方法中覆盖区域越来越小所以定位精度越来越高。本文方法不受节点数量的影响，维持在90%的水平。

图9 参考节点数量变化

选取20个参考节点与20个未知节点，节点通信半径在1～10 m内变化，在10 m×10 m的方形范围内进行定位测试。设置实际位置与估计未知距离在2 m内的为定位成功。横坐标为节点通信半径，纵坐标为定位成功率。如图10所示随着节点的通信半径逐渐增大，RSSI方法和几何方法的定位精度逐渐减小。节点通信半径越大，未知节点能够监测到的参考节点越多，参考节点越多，在密集的区域内会影响定位精度。本文方法限制了未知节点监测的参考节点数量，参考节点的上线数量为3个，所以并不受此干扰因素的影响。

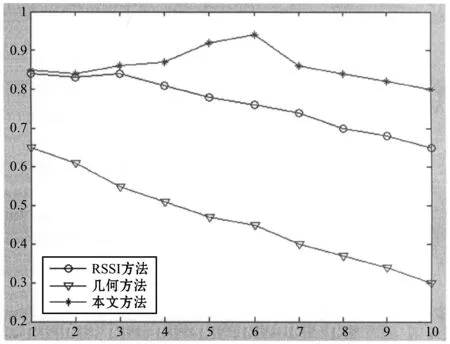
图10 参考节点通信半径变化

3.2 医院场景运行检测

如图11所示中红圈内为实际定位产品。其功能是保障医疗器械、医院资产的安全，监控医疗设备的使用情况等。

图11 实际产品图

几何方法在实际运用当中定位精度远远不能满足商业需求，所以这里并没用将几何方法加入实际检测当中。图12中RSSI方法的实际运用，采用的是三边定位方法。其中方形点表示的是医疗器械的估计位置。我们在处置室存放了11台医疗设备，每个设备都贴有定位产品。通过图很明显能够看出11台设备处于5个不同的位置，但是实际情况是11台设备都处于同一地点。产生此类现象的原因是医院环境内参考节点都布置在楼层的集成吊顶内，未知节点处于房间内。未知节点与参考节点不处于同一个平面；未知节点与参考节点中间间隔两堵墙；未知节点与参考节点之间存在大量人员流动。所以上位机收集的RSSI值一直处于变动状态，导致了多个节点的定位错误。

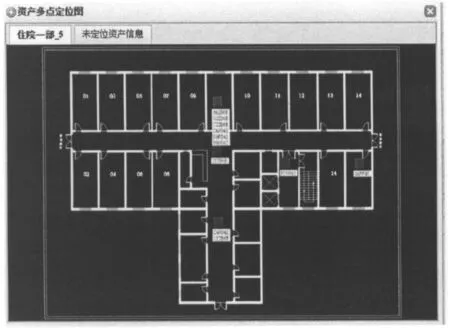
图12 基于RSSI值定位效果

图13是改进后的基于RSSI值定位算法。对RSSI值进行了滤波、去抖，去除了奇异值点和扰动。图中6个未知节点都处于同一位置，但图中仍然显示了6个未知节点处于4个不同的地方。但图中很明显看到误差范围减小，未知节点的误差区域缩小了。去除了环境因素的影响可以提高定位精度。但此种定位精度仍然不能满足实际运用的需求。

图14中是采用了本文算法后的定位效果截图。两个未知节点摆放在护士站附近位置，实际位置与估计位置误差1 m左右，定位精度可以满足实际运用需求。

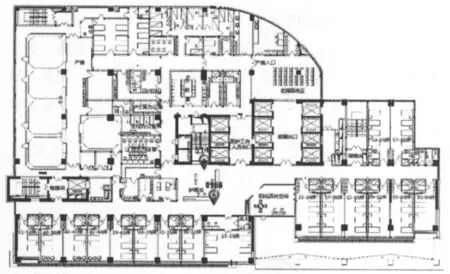
图14 基于本文方法定位效果

4 结 语

本文提出了一种几何估算与RSSI值相结合的定位算法。有效弥补了几何估算方法的不足。并进行了仿真测试和实际测试。与RSSI方法和几何方法进行了详细的对比和分析。结果表明本文方法要优于其他两种定位方法。定位精度和稳定性都有显著的提升。在实际运用当中也取得了良好的定位效果。

[1] Want R,Hopper A,Falcao V,et al. The active badge location system[J]. ACM Transactions on Information Systems, 1992, 10(1):91-102.

[2] 杨云涛, 石志勇, 关贞珍,等. 地磁场在导航定位系统中的应用[J]. 中国惯性技术学报, 2007, 15(6):686-692.

[3] 刘琪, 闫丽, 周正. UWB的技术特点及其发展方向[J]. 现代电信科技, 2009, 39(10):6-10.

[4] 易前旭. 移动蜂窝网络的无缝切换技术[J]. 无线互联科技, 2014(7):32-32.

[5] 张利. 基于WiFi技术的定位系统的设计与实现[D]. 北京：北京邮电大学，2009.

[6] 林琪. “LiFi”,让灯泡变成无线路由[J]. 环境, 2013(11):77-79.

[7] 王茜, 王岩.无线城域网WiMAX技术及其应用[J].电信科学, 2004, 20(8)：27-30.

[8] 周怡颋, 凌志浩, 吴勤勤.ZigBee无线通信技术及其应用探讨[J].自动化仪表, 2005, 26(6)：5-9.

[9] 马建仓, 罗亚军, 赵玉亭.蓝牙核心技术及应用[M].北京: 科学出版社, 2003.

[10] 蒋挺, 赵成林. 紫蜂技术及其应用[M].北京：北京邮电大学出版社, 2006.

[11] 任克强, 庄放望. 移动锚节点凸规划定位算法研究及改进[J]. 传感技术学报, 2014(10)：1406-1411.

[12] 周怡颋, 凌志浩, 吴勤勤. ZigBee无线通信技术及其应用探讨[J].自动化仪表, 2005, 26(6)：5-9.

[13] 彭宇, 王丹.无线传感器网络定位技术综述[J].电子测量与仪器学报, 2011, 25(5)：389-399.

[14] Blanco L, Serra J, Najar M. SPC12-2: Low Complexity Toa Estimation for Wireless Location[C]// Global Telecommunications Conference, 2006. GLOBECOM’06, San Francisco, Ca, Usa, 27 November-1 December. DBLP, 2006:1-5.

[15] 史小红.基于TDOA的无线定位方法及其性能分析[J].东南大学学报, 2013, 43(2)：252-257.

[16] 方震, 赵湛, 郭鹏, 等.基于RSSI测距分析[J].传感器学报, 2007, 20(11)：2526-2530.

[17] 陈维克,李文锋,首珩, 等.基于RSSI的无线传感器网络加权质心定位算法[J]. 武汉理工大学学报(交通科学与工程版), 2006, 32(2): 265-268.

[18] Li J, Zhang J, Xiande L. A Weighted DV-Hop Localization Scheme for Wireless Sensor Networks[C]// International Conference on Scalable Computing and Communications; Eighth International Conference on Embedded Computing. IEEE Computer Society, 2009:269-272.

[19] Zhou Y, Ao X, Xia S. An improved APIT node self-localization algorithm in WSN[C]// Intelligent Control and Automation, 2008. Wcica 2008. World Congress on. IEEE, 2008:7582-7586.

INDOOR LOCATION ALGORITHM BASED ON GEOMETRICAL ESTIMATION AND RSSI

Xu Chi1Qiu Tian2Cao Guangcheng1

1(ShanghaiInstituteofTechnology,Shanghai201418,China)2(ShanghaiKyeeCo.,LTD,Shanghai200240,China)

This paper presents a new method based on geometric estimation and RSSI. The location of the unknown node can be estimated by the communication range of the reference node. An unknown node location can be estimated by reference to the communication overlap area of the node. The RSSI value optimization is introduced based on the geometric estimation method. The RSSI value is used to divide the geometric estimation region, and the new unknown node position is calculated by using the improved formula. The experimental results show that the proposed scheme is superior to the basic localization algorithm and has a high accuracy. At the same time, a preliminary system test is conducted in the hospital scene which gets a good positioning effect.

Geometrical estimation RSSI Indoor localization

2016-05-15。徐驰，硕士，主研领域：室内定位。邱添，学士。曹广成，硕士。

TP3

A

10.3969/j.issn.1000-386x.2017.06.053