基于改进果蝇算法求解混合整数非线性规划问题

朱志同 赵 阳 李 炜, 郭 星,

1(安徽大学计算智能与信号处理重点实验室 安徽 合肥 230039)2(安徽大学计算机科学与技术学院 安徽 合肥 230601)

基于改进果蝇算法求解混合整数非线性规划问题

朱志同1赵 阳2李 炜1,2郭 星1,2

1(安徽大学计算智能与信号处理重点实验室 安徽 合肥 230039)2(安徽大学计算机科学与技术学院 安徽 合肥 230601)

在科学及工程系统设计中存在许多混合整数非线性规划MINLP(Mixed-Integer NonLinear Programming)问题，该类问题变量类型丰富且约束条件较多，难以求解，为此提出一种改进果蝇算法。该算法对不同类型变量的更新采取不同的策略，并采用周期性的步长函数指导果蝇的寻优，使其避免陷入局部最优。并通过与另外两种常用的算法在稳定性、收敛速度等方面进行了比较，实验结果表明该改进的果蝇算法效果较优，能有效地解决MINLP问题。

混合整数非线性规划 智能计算 果蝇算法

0 引 言

在科学及工程系统设计中存在许多问题都是非线性规划问题，其中混合整数非线性规划MINLP又是非线性规划的一个重要分支[1]。混合整数非线性规划是同时包含离散性变量和连续性变量的优化问题，许多组合优化问题如：TSP问题、0-1背包问题等都可视为MNLP问题。对于MNLP问题，其目标函数和约束条件的非线性，使得结果往往存在局部最优解[2]。

解决MINLP主要有确定性方法和随机性方法[3]。确定性方法如分枝定界法(B&B)、外逼近法(OA)、广义Bender分解法(CBD)，但这些方法局限性很大：一是计算量太大；二是不利于编程求解。如分枝定界法取消或放宽原问题的约束，并将改变后的问题分解成多个子问题进行求解，以此确定原问题的最优解或其最优解所在的区间，由此可以看出该方法不适宜用编程的方法去求解。近年来，越来越多的随机性方法应用于MINLP，如遗传算法(GA)、差分进化算法(DE)、粒子群算法(PSO)等[4-5]。但这些方法也各有缺点，例如：遗传算法易于早熟且计算量大；差分进化算法过于复杂且计算耗时多；粒子群算法容易陷入局部最优[6]。

潘文超[7]于2011年提出了果蝇优化算法FOA (Fruit Fly Optimization Algorithm)。该算法也属于群智能算法的一种，作为新型的进化算法，与其他算法相比，FOA在先天上就有很多优势，易于理解且实现简单，全局寻优能力强且收敛速度快，但缺点在于稳定性不足，易于陷入局部最优[8]。随着研究的深入，很多学者对果蝇算法进行了改进，在保持其优势的情况下，尽量提高其稳定性及跳出局部最优的能力。目前已有研究，大多是求解连续性问题，没有应用于解决具有离散变量的实际问题[9]。本文通过改进果蝇算法，使之能有效地解决混合整数非线性规划这一实际问题[10-11]。

1 果蝇算法

1.1 基本果蝇算法

果蝇算法是基于动物群体觅食行为演化出的一种全局寻优新方法。果蝇在视觉和嗅觉上优于其他物种，其发现食物行为的特点包括：① 果蝇个体使用嗅觉器官分辨食物的气味来源并朝这个方向飞行；② 果蝇在飞行过程中使用视觉去寻找食物[12]。

其具体过程如下：

① 初始化参数，果蝇种群数量(mSize)，迭代次数(pSize)，飞行范围也即自变量的定义域(dom)。

② 随机初始化果蝇群位置(xis,yis):

xis=rand(dom)

(1)

yis=rand(dom)

(2)

③ 果蝇个体先使用嗅觉分别食物气味的方向并立即飞向该方向，再使用视觉发现该食物，RandomValue为[-1,1]上的随机值，其值的正负表示果蝇飞行的方向，大小表示果蝇飞行的距离:

xi=xis+RandomValue

(3)

yi=yis+RandomValue

(4)

④ 计算每只果蝇当前位置与原点的距离(disti)及食物的气味浓度值(si):

(5)

(6)

⑤ 将si代入到目标函数中，求出该位置上食物的气味浓度值(smelli):

smelli=function(si)

(7)

⑥ 在果蝇群中找出气味浓度值最大的果蝇个体:

[bestsmell bestindex]=max(smelli)

(8)

⑦ 保留最大气味浓度值，所有果蝇向该位置聚集，并将该位置更新为果蝇群的新位置:

Bestsmell=bestsmell

(9)

xis=x[bestindex]

(10)

yis=y[bestindex]

(11)

⑧ 判断算法是否达到结束标志，若是则结束，否则重复执行步骤③-步骤⑥，判断当前果蝇群中最优的气味浓度值是否优于历史最优气味浓度值，若是则执行步骤⑦。

1.2 改进的果蝇算法

由1.1节基本果蝇算法的流程可以看出，该算法在果蝇个体的更新方式及计算上存在不足，具体如下：

1) 式(3)、式(4)在连续域上采用随机数方式更新果蝇个体位置，使得果蝇寻优的效率较为低下；

2) 在连续域上取值不能适用于离散域，适用范围较窄；

3) 式(5)、式(6)是计算当前位置与原点间的距离，不能适用于最优点不是原点的情况。

为此，我们要用其解决混合整数非线性规划问题，必须对其进行改造。针对基本果蝇算法的不足，改进主要有以下三个方面：

1) 对不同类型变量采取不同的更新方式，如式(14)、式(15)，解决了变量类型与更新方式不匹配的问题。

2) 采取步长函数指导果蝇位置的更新，如式(16)、式(17) ，使果蝇在寻找最优解的过程不再具有随机性，可以加快收敛，参数α为连续型变量的指导参数，取值范围为0.5～0.95，β为离散型变量的参数，取值范围为0.2～0.5。并且该函数具有周期性，可以提高果蝇跳出局部最优解的能力，更好地找出全局最优解，参数T为其周期，取值范围为20～40，T值越小，函数震荡越强，T值越大，函数精度越高。p为当前的迭代次数。

3) 去除式(5)和式(6)，将变量直接带入所求函数中，如式(18)，简化了计算。

下面是改进的果蝇算法的详细步骤：

① 初始化参数，果蝇种群数量(mSize)，迭代次数(pSize)，步长函数的参数α、β、p、T，果蝇在变量j的飞行范围(domj∈[domL,j,domu,j])。

② 随机生成果蝇群的初始位置，其中，xaxi,j为连续型变量，yaxi,j为离散型变量:

xaxi,j=rand(domj)

(12)

yaxi,j=⎣rand(domj)」

(13)

③ 果蝇个体中各种变量的更新规则，即其使用嗅觉及视觉发现食物，如xi,j代表第i只果蝇中的第j个变量,randomvalue∈[-1,1]:

xi,j=xaxi,j+αj×randomvalue

(14)

yi,j=⎣yaxi,j+βj×randomvalue」

(15)

αj=|domU,j-domL,j|×αp%T

(16)

βj=|domU,j-domL,j|×βp%T

(17)

④ 将xi,j、yi,j代入目标函数中，求出该果蝇此时位置上的气味浓度(smelli):

smelli=Function(xi,j,yi,j)

(18)

⑤ 找出果蝇群中气味浓度最优的果蝇个体:

[bestsmell bestindex]=max(smelli)

(19)

⑥ 保留最优气味浓度值及该果蝇的位置，所有果蝇都飞向该位置:

bestSmell=bsetsmell

(20)

xaxi,j=x[bestindex]

(21)

yaxi,j=y[bestindex]

(22)

⑦ 判断算法是否到达结束标志，若是则结束算法，否则重复步骤③-步骤⑤，并判断当前果蝇群中最优气味浓度是否优于历史值，若是则还回步骤⑥。

对比基本算法与改进的算法可知，本文从基本算法的不足与所研究问题的特点出发，有针对性地提出了周期性震荡函数指导果蝇飞行，以及分离不同类型变量的更新方式，从而能有效地解决所研究的问题。

2 数值实验与分析

本文选取四个混合整数非线性规划问题进行仿真[13-14]，该类函数是由实际的工程问题抽象而成。并且选取的函数具有很强的检验性，第一个测试用例连续性的变量多于离散性的变量，而第二个测试用例则相反，这样可以综合的检验出改进算法的性能。并将改进算法与粒子群算法[15](PSO)及差分进化算法[16](DE)进行了比较。PSO算法中惯性约束系数W=0.5，加速系数c1=2、c2=2；DE算法中变异算子F=0.5，交叉算子CR=0.15。PSO及DE的种群数与迭代数均和果蝇算法一致。果蝇群数量mSize=100，迭代次数pSize=1 000，步长参数α=0.65、β=0.35、T=20，p为当前的迭代次数。该实验的计算机配置与环境为：英特尔CPU、3.5GHz，8GB内存，Win7 64位操作系统。本文主要从算法的稳定性、收敛速度及最优解的精度等方面与粒子群算法(PSO)及差分进化算法(DE)进行了综合的比较。本文算法在下文图中用OURS表示。

2.1 混合整数非线性规划问题

混合整数非线性规划其一般形式为：

minf(x,y)

(23)

其中，m、n分别表示不等式约束或等式约束的个数，x表示ne维连续变量，y表示nc维整数或离散变量。

(1) 测试用例1：

minf1(x,y)=-y+2x-In(x/2)

(24)

最优解为(x.y)=(1.375,1)，最优值为2.214。

(2) 测试用例2：

min f2(x,y)=-0.7y+5(x1-0.5)2+0.8

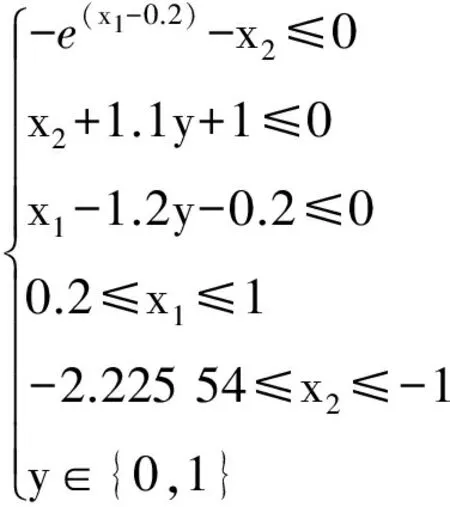
(25)

最优解为(x1,x2,y)=(0.941 94,-2,1)，最优值为1.076 54。

(3) 测试用例3：

minf4(x,y)= 0.622 4(0.062 5y1)x1x2+

3.166 1(0.062 5y1)2x2+

19.84(0.062 5y1)2x1

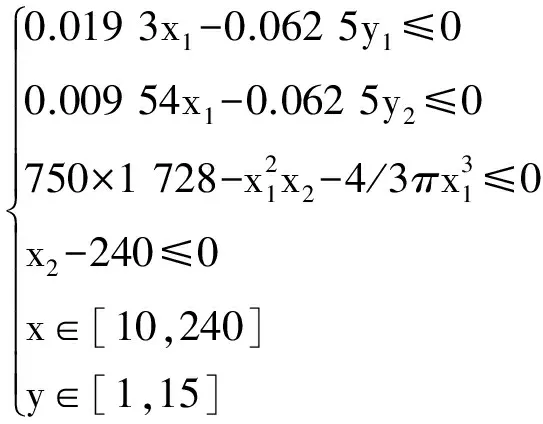
(26)

已知最优解为(x1,x2,y1,y2)=(38.860 1,221.365,12,6)，最优值为5 850.38。

(4) 测试用例4：

minf3(x,y)= (y1-1)2+(y2-1)2+

(y3-1)2-In(1+y4)+

(x1-1)2+(x2-2)2+(x3-3)2

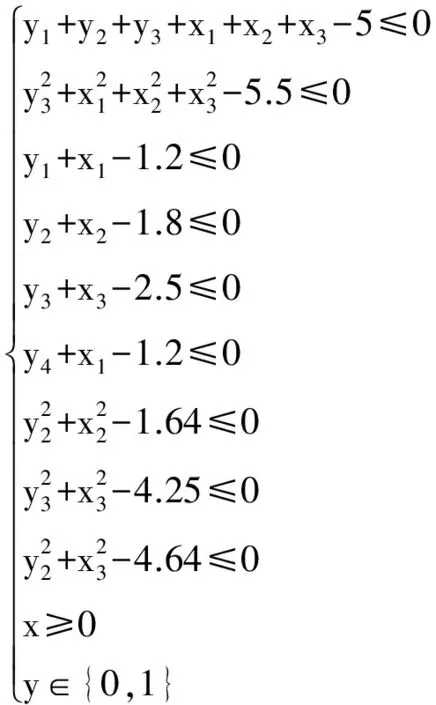
(27)

已知最优解为：(x1,x2,x3,y1,y2,y3,y4)=(0.2,1.280 624,1.954 483,1,0,0,1)，最优值为3.557 463。

2.2 实验结果与分析

本文从以下几个方面来对比各种算法在解决上述两个测试用例时的性能。图1-图4表示三种算法在迭代次数为1 000时算法的寻优情况。其横坐标表示为1 000次迭代数据每20次取样所形成的50个样本数，纵坐标为每个取样样本上的函数最优值。

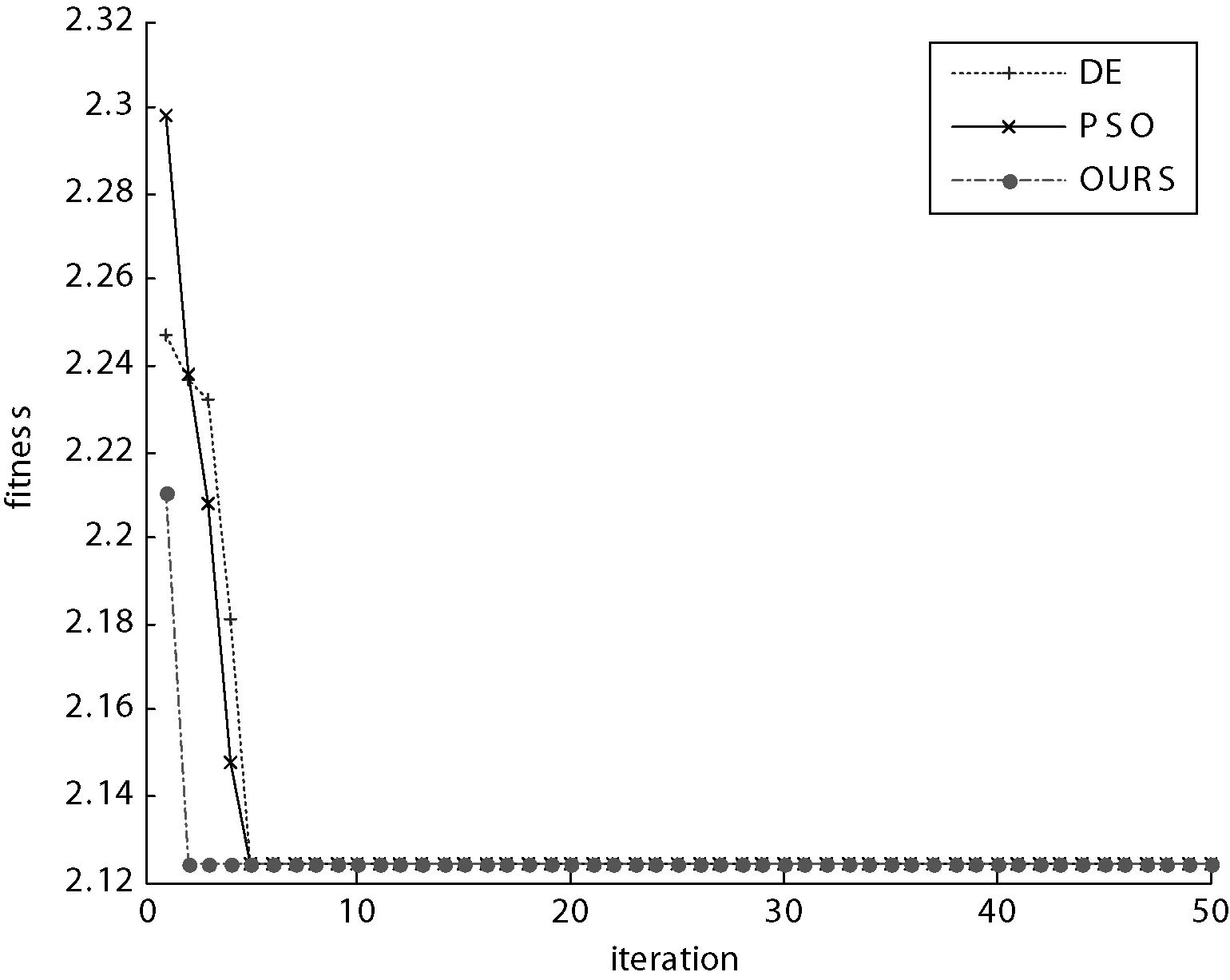
图1 三种算法解决测试用例1的性能对比图

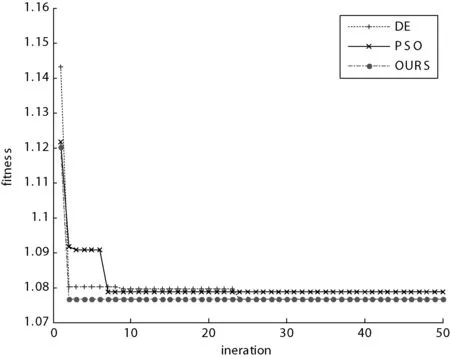
图2 三种算法解决测试用例2的性能对比图

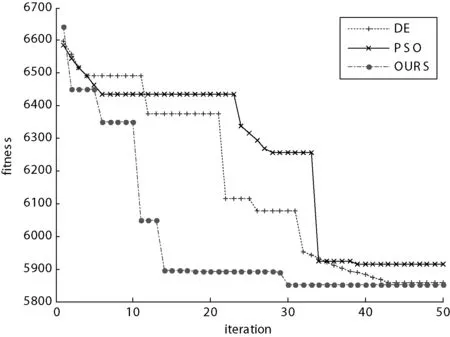
图3 三种算法解决测试用例3的性能对比图

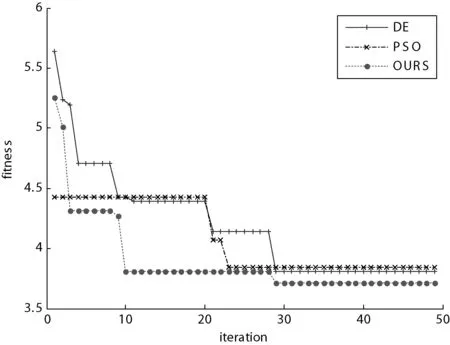
图4 三种算法解决测试用例4的性能对比图

从图1和图2中可以看出，由于函数f1及函数f2的变量较少，离散性变量不多于连续性变量，并且变量的域间较小，所以从图1和图2上可以看出三种算法在对此类型的问题求解的效率较高、效果也较好。但是，本文算法(图中的OURS)从收敛速度来看，性能明显比其他两种要好。其原因一是函数的特点造成的，二是改进的果蝇算法中加入了步长函数可以指导果蝇的飞行，加快果蝇寻找到最优值。图3中函数f3的变量类型的个数相同，但是，变量的域间距较大。从图3中可以看出本文算法优于DE及PSO算法。图4中函数f4的离散性变量多于连续性变量，从图中可以看出三种算法都在某一段时间内陷入了局部最优，但改进的果蝇算法最后能找到最优值，而其他算法在面对多离散性变量问题时效果就不是那么好了。

图5-图8表示了三种算法迭代次数分别为100、500和1 000次，独立运行50次时，得到的50个最优值中达到所规定的误差精度的成功次数占总次数的比例。其中达到函数f1、f2的规定最优值的误差精度为1%，而函数f2、f4的误差精度为5%。

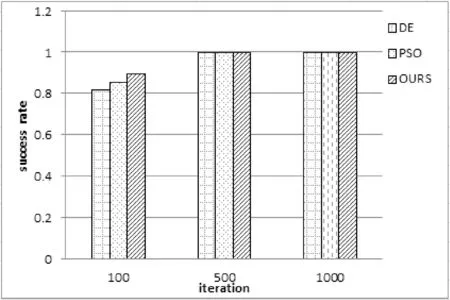
图5 三种算法解决测试用例1的性能对比图

图6 三种算法解决测试用例2的性能对比图

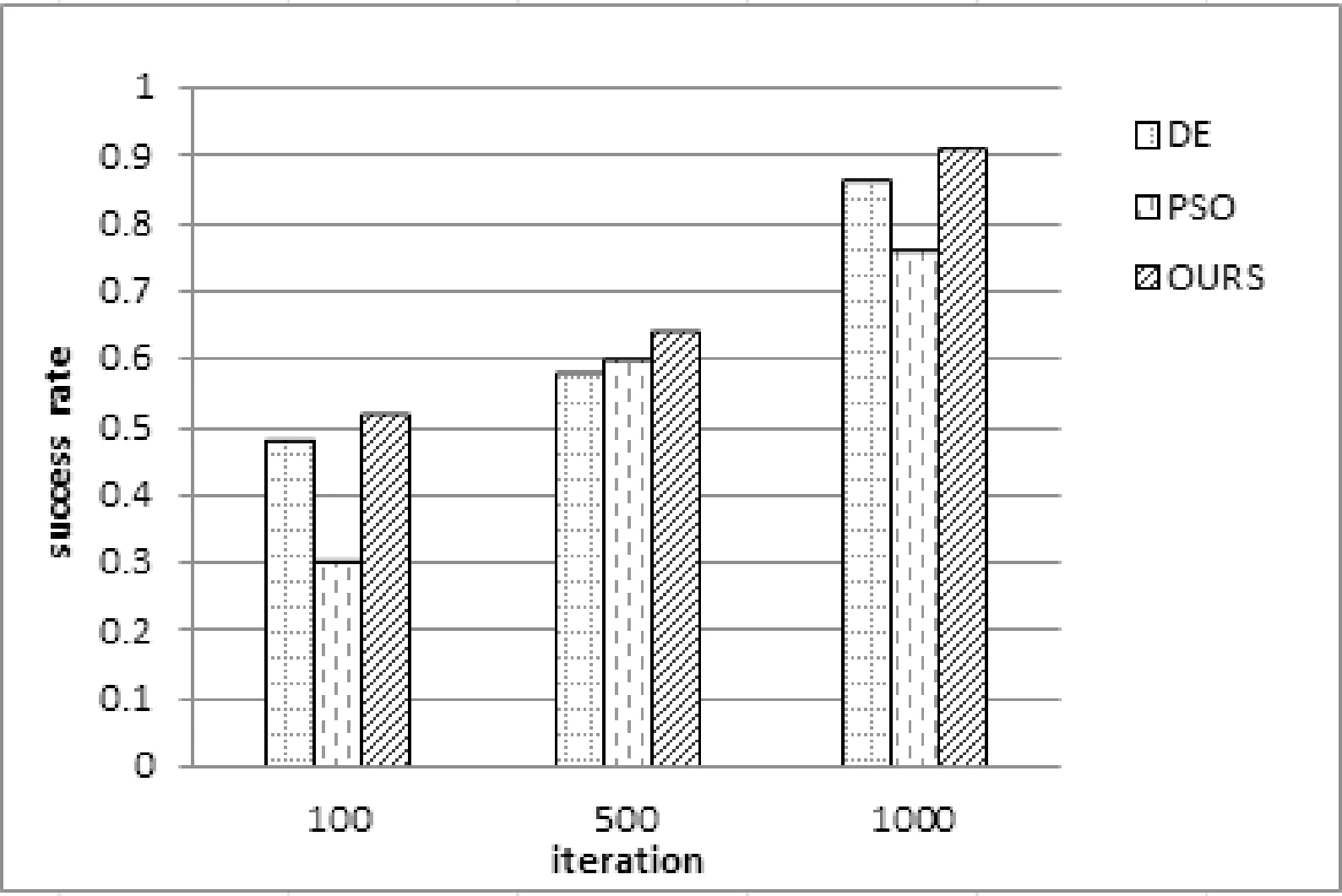
图7 三种算法解决测试用例3的性能对比图

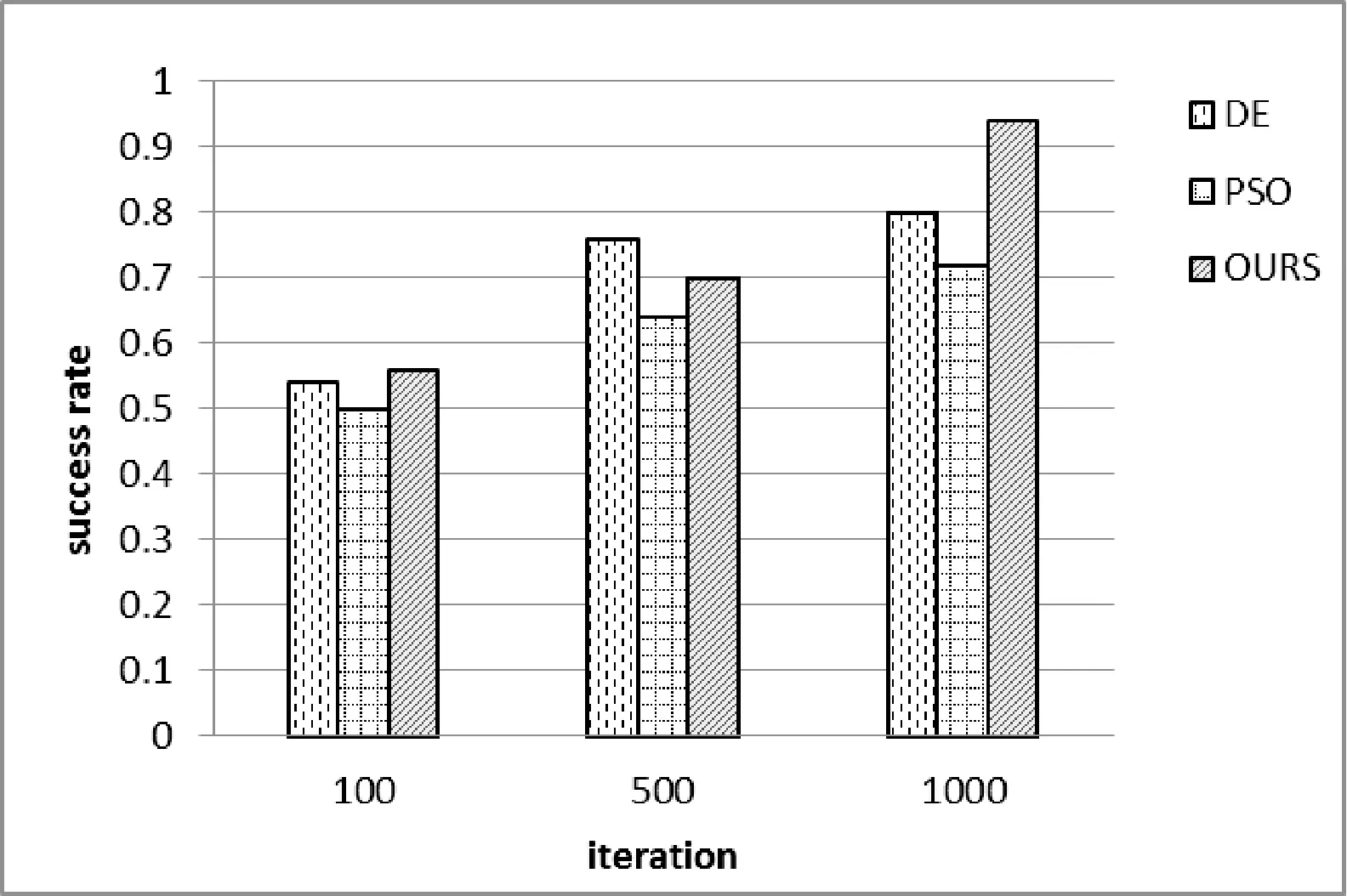
图8 三种算法解决测试用例4的性能对比图

从图5-图8的直方图可以得出这三种算法在解决不同复杂度的函数时，它们的效率及成功率也不相同，对于较复杂的离散变量，改进的果蝇算法有较高的成功率，表明算法的稳定性较强。

表1表示了该三种算法它们独自运行50次，每次迭代1 000次时的实验结果，从表中可以看出，本算法比其他两种算法稳定性较好，且精度要高。

表1 三种算法最优值与最差值对比表

3 结 语

本文提出了一种求解混合整数非线性规划问题的改进果蝇算法，该算法通过分离不同类型的变量，且对变量的更新方式设置不同的步长约束函数，使得该改进的算法能有效地提高稳定性、避免陷入局部最优。实验结果表明，改进的果蝇算法比其他算法在求解此类非线性规划问题上的收敛速度快、精度高。然而，该改进的果蝇算法的适应性较低，虽对所求解问题的效果较好，但对其他规划问题的求解还有待深入的研究。

[1]ZhangXS.Introductiontomathematicalprogramming[J].Introductiontomathematicalprogramming,2000,46(4071):273-298.

[2] 张莉,冯大政,李宏.求解整数非线性规划结合正交杂交的离散PSO算法[J].控制与决策,2012,27(9):1387-1387.

[3] 刘明明,崔春风,童小娇,等.混合整数非线性规划的算法软件及最新进展[J].中国科学:数学,2016(1):001.

[4] 刘振泽,许洋,王峰明.改进差分进化算法在非线性模型预测控制中的应用[J].北京工业大学学报,2015,41(5):680-685.

[5]GuoX,LiX.AGeneticAlgorithmforaClassofFractionalBilevelProgrammingProblemswithIntervalCoefficients[J].AdvancesinAppliedMathematics,2015,4(1):63-69.

[6] 吴小文,李擎.果蝇算法和5种群智能算法的寻优性能研究[J].火力与指挥控制,2013,38(4):17-20.

[7] 潘文超.应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J].太原理工大学学报(社会科学版),2011,29(4):1-5.

[8]YuanX,DaiX,ZhaoJ,etal.Onanovelmulti-swarmfruitflyoptimizationalgorithmanditsapplication[J].AppliedMathematics&Computation,2014,233(3):260-271.

[9]PanWT.AnewFruitFlyOptimizationAlgorithm:Takingthefinancialdistressmodelasanexample[J].Knowledge-BasedSystems,2012,26(2):69-74.

[10] 郑晓龙,王凌,王圣尧.求解置换流水线调度问题的混合离散果蝇算法[J].控制理论与应用,2014,31(2):159-164.

[11] 杨书,舒勤,何川.改进的果蝇算法及其在PPI网络中的应用[J].计算机应用与软件,2014,31(12):291-294.

[12]ShanD,CaoGH,DongHJ.LGMS-FOA:AnImprovedFruitFlyOptimizationAlgorithmforSolvingOptimizationProblems[J].MathematicalProblemsinEngineering,2013,2013(7):1256-1271.

[13]LinYC,HwangKS,WangFS.Amixed-codingschemeofevolutionaryalgorithmstosolvemixed-integernonlinearprogrammingproblems[J].Computers&MathematicswithApplications,2004,47(8-9):1295-1307.

[14]DeepK,SinghKP,KansalML,etal.Arealcodedgeneticalgorithmforsolvingintegerandmixedintegeroptimizationproblems[J].AppliedMathematics&Computation,2009,212(2):505-518.

[15] 唐俊.PSO算法原理及应用[J].计算机技术与发展,2010,20(2):213-216.

[16] 梅觅,薛惠锋,谷雨.旅行商问题的改进差分进化方法[J].信息技术,2011(2):20-23.

SOLVING MIXED INTEGER NONLINEAR PROGRAMMING BASED ON THE IMPROVED FRUIT FLIES ALGORITHM

Zhu Zhitong1Zhao Yang2Li Wei1,2Guo Xing1,2

1(KeyLaboratoryofICSP,MinistryofEducation,AnhuiUniversity,Hefei230039,Anhui,China)2(SchoolofComputerScienceandTechnology,AnhuiUniversity,Hefei230601,Anhui,China)

There are many MINLP problems in the design of science and engineering systems, which are rich in variables and have many constraints and are difficult to solve. Therefore, this paper proposes an improved fruit flies algorithm. The algorithm uses different strategies to update different types of variables, and uses the periodic step function to guide the optimization of FOA so as to avoid falling into local optimization. Compared with the other two commonly used algorithms in terms of stability, convergence speed and so on, experimental results show that the improved fruit flies algorithm can effectively solve the MINLP problems.

Mixed integer nonlinear programming Smart computing Fruit flies algorithm

2016-06-24。国家科技支撑计划项目(2015BAK24B00)。朱志同，硕士生，主研领域：智能计算，信号处理。赵阳，本科生。李炜，教授。郭星，博士。

TP301.6

A

10.3969/j.issn.1000-386x.2017.06.047