未知状态模型下基于高阶容积卡尔曼滤波和神经网络的状态估计算法

许大星 王海伦,2

1(衢州学院电气与信息工程学院 浙江 衢州 324000)2(上海海事大学物流工程学院 上海 201306)

未知状态模型下基于高阶容积卡尔曼滤波和神经网络的状态估计算法

许大星1王海伦1,2

1(衢州学院电气与信息工程学院 浙江 衢州 324000)2(上海海事大学物流工程学院 上海 201306)

针对非线性系统状态模型未知的情形,提出一种基于高阶容积卡尔曼滤波和神经网络的状态估计算法，解决了未知非线性系统模型的状态估计问题。在算法的实现过程中，首先利用神经网络对非线性系统建立状态空间模型，然后把神经网络的权重和系统的状态变量组合在一起作为新的状态变量，并采用高阶容积卡尔曼滤波对新的状态进行实时更新，从而达到神经网络对非线性系统模型的真实逼近以及对状态值的精确估计。最后的目标跟踪仿真表明，该算法具有更高的估计精度。

非线性系统 未知模型 高阶容积卡尔曼滤波 神经网络

0 引 言

根据连接的拓扑结构，神经网络模型可分为前向神经网络和后向神经网络。20世纪80年代，Rumelhard等基于前向神经网络提出误差反向传播算法，因其算法结构简单，易于实现且具有很强的非线性映射能力，已广泛应用在航空航天、智能交通、模式识别以及医学工程等领域中[1]。

当系统模型未知时，采用神经网络对模型进行非线性近似是一种简单而有效的方法。神经网络根据实际数据集确定网络逼近的非线性函数，然而，当实际系统的状态变量不完全可测时，单独采用神经网络将无法建立过程的模型。状态空间模型法对系统的内部状态和外部可观测输出变量之间的变化关系进行描述。由于该方法可以对系统内部复杂的状态进行估计和预测，因此已经被广泛地应用在动态系统的处理当中。对系统的状态空间模型建立完成之后，就需要利用合适的方法对系统的状态进行估计。滤波方法在状态空间中利用系统输入输出观测数据，对系统状态进行最优估计[2]。这种滤波的方法不仅可以对状态进行估计，还可以对神经网络系统参数进行辨识。

非线性滤波算法在参数估计中得到了长足的发展，特别是在神经网络的参数辨识方面，其将网络的权系数参数看作特殊的状态进行估计。文献[3]首先利用神经网络建立状态空间模型，将网络权系数作为系统的状态变量，进而基于扩展卡尔曼滤波算法对状态变量进行实时更新。仿真实验表明，其效果明显优于传统的误差反向传播算法，特别是存在明显噪声的干扰下更能取得较高的估计精度。扩展卡尔曼滤波是目前应用最为广泛的一种非线性滤波方法，然而当系统的非线性程度较高，一阶近似会带来非常大的截断误差，扩展卡尔曼滤波算法的估计性能将随之大大下降，甚至发散[4]。由于扩展卡尔曼滤波稳定性差、精度低等缺点，Julier等提出了无迹卡尔曼滤波，使用无迹变换来处理均值和方差的非线性传递[5]。已经有不少学者利用无迹卡尔曼滤波和神经网络来解决未知系统模型的非线性系统状态估计问题。文献[6]提出了应用无迹卡尔曼滤波算法对神经网络权系数进行在线估计。文献[7]对基于扩展卡尔曼滤波和无迹卡尔曼滤波的神经网络算法进行了实验对比，结果表明，基于无迹卡尔曼滤波算法的神经网络算法明显优于基于扩展卡尔曼滤波算法的神经网络算法。然而无迹卡尔曼滤波的精度仍然有限，当系统维数较高时，其估计性能明显降低。为了进一步提高状态的估计精度，文献[8]提出了一种基于任意阶容积规则的高阶容积卡尔曼滤波，分别使用Genz积分方法和矩匹配法推导出任意阶的球面规则和相径规则，从而构造高阶球面-相径容积规则来计算高斯型积分，并建立高阶容积卡尔曼滤波算法。文献[9]对无迹卡尔曼滤波算法和高阶容积卡尔曼滤波算法的精度和适用范围进行了对比，结果表明，高阶容积卡尔曼滤波算法对高维系统适用性更强，估计误差更小。

基于此，本文针对未知状态模型的非线性系统，首先利用神经网络建立状态空间模型，将网络的权系数和系统的状态组合一起为增广的状态变量。然后采用高阶容积卡尔曼滤波算法对神经网络系统状态进行估计预测，从而实现网络权系数的自适应调整和状态的实时更新。

1 神经网络的状态空间模型

神经网络的结构模型一般可分为前馈神经网络模型、反馈神经网络模型以及随机神经网络模型等。目前在各个行业领域中前馈神经网络模型应用最为广泛，其状态空间的模型结构如图1所示。

图1 神经网络的模型结构

图1中，x1,x2,…,xn用来表示输入的样本节点，y1,y2,…,ym用来表示输出样本节点，θ1,θ2,…,θq表示权重系数。该神经网络模型结构共有三个节点层，分别为输入层、隐层和输出层，各个层之间通过权系数进行连接，输入输出层在两端，中间隐含层的节点数根据实际要求进行选取。

2 高阶容积卡尔曼滤波原理

首先考虑如下离散非线性系统：

xk=f(xk-1)+wk

(1)

zk=h(xk)+vk

(2)

其中，xk为n维的状态向量；zk为m维的观测向量；函数f，h为已知的非线性函数；{wk}与{vk}均为独立的零均值高斯白噪声。

对于一般的非线性系统，在高斯假设下可将贝叶斯估计基本理论与任意阶容积规则相结合，从而推导出高阶的容积卡尔曼滤波。与无迹卡尔曼滤波结构相同，同样分为状态预测(时间更新)和测量更新两个步骤，主要是高阶容积卡尔曼滤波利用容积点逼近状态的后验分布。该算法具有精度高、稳定性强、参数选取简单的优点。文献[9]对比了UKF算法和CKF算法的精度和适用范围,表明CKF算法效率更高,尤其是对高维系统的适用性更强。高阶容积规则满足：

(3)

(4)

(5)

(6)

(7)

(8)

3 基于高阶容积卡尔曼滤波和神经网络的状态估计

当系统的模型未知时，采用神经网络对系统模型进行建模逼近，那么就需要求解最优的网络节点权系数，同时状态也是未知的。然而，状态与权系数是彼此联系的，因此，本文将系统的状态和权系数组合在一起作为新的状态空间，将原来的系统方程和权系数方程的增广方程作为新的系统模型，进而利用高阶容积卡尔曼滤波算法对状态和权系数实时估计，具体的系统原理如图2所示。

图2 状态估计系统

图2中，在k-1时刻，原系统的状态xk-1与权系数Wk-1组合成新的增广状态向量[xk-1Wk-1]，输入到神经

网络中，进而高阶容积卡尔曼滤波根据增广状态和神经网络的输出结果进行时间更新步骤。最后高阶容积卡尔曼滤波结合时间更新的结果和测量的输出结构进行时间更新得到k时刻的系统增广状态值[xkWk]，并作为下次系统的输入状态。具体算法如下：

首先将系统的状态与神经网络的权系数组合起来，形成增广状态xa=[xW]T，则可建立如下所示的非线性系统：

(9)

(10)

其中，fj(xk)为神经网络对非线性系统建立的数学模型：

(11)

g(x)为神经网络Sigmod核函数，Wk为神经网络的权系数，新系统的过程噪声wk和观测噪声vk均为独立的零均值高斯白噪声，并且对应的协方差矩阵分别为Qk、Rk。

然后对状态进行时间更新：

1) 在时刻k，假设k-1时刻的误差协方差已知且为Pk-1|k-1，分解因数：

(12)

其中，向量Sk-1|k-1为Pk-1|k-1的Cholesky分解。

2) 计算容积点：

(13)

其中m=2n，向量ξi为：

(14)

(15)

3) 计算状态方程传播后的容积点(i=1,2,…,m)：

(16)

4) 计算一步状态预测：

(17)

其中，权值wi分别为：

(18)

5) 计算一步预测误差协方差矩阵：

(19)

最后进行测量更新：

1) 分解因数：

(20)

2) 计算更新后的状态容积点：

(21)

3) 计算测量方程传播后的容积点：

(22)

4) 计算k时刻一步量测预测：

(23)

5) 计算新息协方差矩阵：

(24)

6) 计算一步预测互协方差矩阵：

(25)

7) 计算增益矩阵：

(26)

8) 计算更新状态：

(27)

9) 计算协方差矩阵：

(28)

4 实验仿真

考虑如下非线性目标跟踪系统离散模型[10]：

(29)

y(k)=x1(k)+x2(k)+v(k)

(30)

为了对比方便，本文对算法进行如下简单标记：

算法1：基于高阶容积卡尔曼滤波和神经网络的估计算法；

算法2：基于无迹卡尔曼滤波和神经网络的估计算法。

仿真结果如图3-图6及表1所示。

图3 状态1的估计曲线

图4 状态2的估计曲线

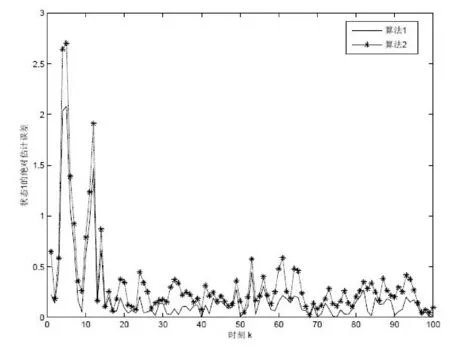
图5 状态1的估计误差曲线

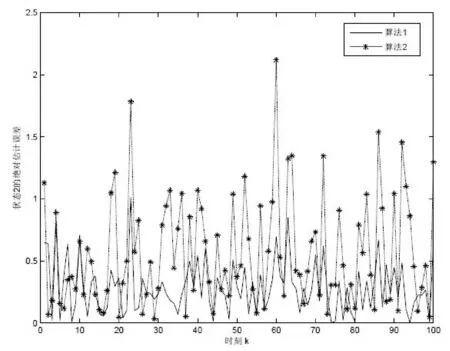
图6 状态2的估计误差曲线

表1 估计误差对比

从图3和图4的估计曲线来看，算法1和算法2都能对原始状态进行较好的跟踪估计，说明两种算法都是有效的。从图4和图5的估计误差曲线来看，两种算法的误差很快趋于稳定，且算法1的误差明显要小于算法2的误差。从表1的统计数据来看，算法1的状态估计精度大大高于算法2，特别是在对状态2的估计精度上，算法2的估计误差是算法1估计误差的两倍多。这主要是因为高阶容积卡尔曼滤波算法的估计精度高于无迹卡尔曼滤波算法，从而说明了基于高阶容积卡尔曼滤波和神经网络的估计算法的有效性。

5 结 语

本文针对状态模型未知的非线性系统，提出了一种基于高阶容积卡尔曼滤波算法和神经网络的状态估计算法，解决了现有的基于非线性滤波和神经网络的算法对状态估计的精度受限的缺陷问题。首先利用神经网络对系统状态进行建模，并利用高阶容积卡尔曼滤波算法对系统状态和神经网络权重组合成的新状态变量进行实时更新估计。所提算法弥补了现有算法的不足，提高了基于神经网络的状态估计精度，仿真实验表明了本文所提算法的有效性。本文所解决的是模型未知且输出为状态的线性组合的情况下， 非线性系统的状态估计问题相对于估计状态为可测量对象的系统，更具有现实意义。但是对于输出为状态的非线性关系的状态估计问题，由于非线性函数中状态与状态的分离和状态的可观性难以确定，是一个更复杂的问题还需进一步的研究。

[1] 彭玉青,赵翠翠,高晴晴.基于RBF神经网络的集成增量学习算法[J].计算机应用与软件,2016,33(6):246-250.

[2] 南敬昌,桑百行,高明明.新颖的神经网络逆建模方法及其应用[J].计算机应用与软件,2016,33(1):147-150.

[3]SinghalS,WuL.TrainingmultilayerperceptionswiththeextendedKalmanalgorithm[M]//AdvanceinNeuralInformationProcessingSystems.California:MorganKaufmannPublisherInc,1989,1:133-140.

[4] 王英博,闫吉府,李仲学.遗传算法优化径向基神经网络的尾矿库安全预测[J].计算机应用与软件,2015,32(3):182-184.

[5] 高宪军,翟林培.GPS/INS组合导航系统的研究[J].光学精密工程,2004,12(2):146-150.

[6]ZhaF,XuJN.IUKFneuralnetworkmodelingforFOGtemperaturedrift[J].IEEETransonSystemsEngineeringandElectronics,2013,24(5):838-844.

[7]WuXD,WangYN.ExtendedandUnscentedKalmanfilteringbasedfeedforwardneuralnetworksfortimeseriesprediction[J].AppliedMathematicalModelling,2012,36(3):1123-1131.

[8]JiaB,XinM,ChengY.High-degreecubatureKalmanfilter[J].Automatica,2013,49(2):510-518.

[9] 张龙,崔乃刚,杨峰,等.高阶容积卡尔曼滤波及其在目标跟踪中的应用[J].哈尔滨工程大学学报,2016,37(4):573-578.

[10]XiongK,ZhangHY,ChanCW.PerformanceevaluationofUKF-basednonlinearfiltering[J].Automatica,2014,42(2):261-270.

STATE ESTIMATION ALGORITHM BASED ON HIGH ORDER CUBATURE KALMAN FILTER AND NEURAL NETWORK WITH UNKNOWN STATE MODEL

Xu Daxing1Wang Hailun1,2

1(CollegeofElectricalandInformationEngineering,QuzhouUniversity,Quzhou324000,Zhejiang,China)2(LogisticsEngineeringCollege,ShanghaiMaritimeUniversity,Shanghai201306,China)

In view of the nonlinear state model of the system is unknown, this paper presents a state estimation algorithm based on high order cubature Kalman filter and neural network to solve the problem of state estimation of unknown nonlinear system model. The neural network is used to establish the state space model for the nonlinear system. Then, the weight of the neural network and the state of the system variables together are combines as the new state variables. And the new state is updated in real time by high order cubature Kalman filter, so as to achieve the neural network on the nonlinear system model of the real approximation and accurate estimation of the state value. The final target tracking simulation shows that the algorithm has higher estimation accuracy.

Nonlinear system Unknown model High order cubature Kalman filter Neural network

2017-01-06。国家自然科学基金项目(61403229)；浙江省科技厅公益项目(2015C33230)。许大星，助教，主研领域：状态估计，非线性滤波。王海伦，副教授。

TP18

A

10.3969/j.issn.1000-386x.2017.06.046