从初中数学图形变换角度来读图

程长宾

江苏省宿迁市宿豫区新庄中心學校

【摘 要】现代社会已处于读图时代，读图能力是初中生的基本能力之一。从运动的观点来读图，初中数学主要是轴对称、平移、旋转三种变换角度来读图，可思维的灵活性和敏捷性、深刻性.有利于增强学生的创新性思维。收到意想不到的效果，可谓“别有洞天，柳暗花明”。

【关键词】图形 变换 读图

现代信息技术的快速发展，带动包涵了丰富信息的图系统日益大众化和国际化，现代社会早已处于读图时代，人们几乎时时刻刻都与图打交道。数学新课程标准提出“数学素养是现代社会每一个公民应该具备的基本素养。”读图能力应该成为公民的生活基本能力之一。

1872 年，德国大数学家克莱茵发表 “爱尔兰根纲领”的演说，这个里程碑式的论断，改变了近两千年来人们用静止的观点研究几何的传统方法。图形的变换是从运动变化的角度去探索和认识图形与几何的性质，欣赏与设计图案。对发展学生空间观念和思维能力的培养起着重要作用。

轴对称、平移、旋转是初中数学中图形变换的三种形式，利用此三种形式可构造出丰富多彩的图形世界。我们在读图的时候，有意识地从运动角度，运用这三种形式来分析研究图形，可收到意想不到的效果，可谓“别有洞天，柳暗花明”。

一、利用轴对称变换来读图

轴对称是指把一个图形沿着某一条直线折叠，如果它能够与另一个图形完全重合，称这两个图形为轴对称，这条直线就是对称轴。

轴对称具有以下性质：一是成轴对称的两个图形全等；二是如果两个图形成轴对称，那么对称轴是对称点连线的垂直平分线。

在遇到有轴对称的图形时，可考虑从轴对称角度来分析研究图形，得出有关线段、角、垂直等方面的数量或位置关系。

二、利用平移变换来读图

平移是指在平面内，将一个图形上的所有点都按照某个方向作相同距离的移动，这样的图形运动叫做图形的平移运动，简称平移。

平移不改变图形的形状和大小。经过平移，对应线段平行（或共线）且相等，对应角相等，对应点所连接的线段平行且相等；在图形中有全等图形而且有平行线时，可考虑从平移角度来研究图形。

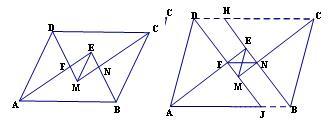
例如（2014沈阳中考数学试题第16题改编）如图，□ABCD中，AB>AD，AE，BE，CM，DM分别为∠DAB，∠ABC，∠BCD，∠CDA的平分线，AE与DM相交于点F，BE与CM相交于点H，连接EM.

求证：EM=AB-AD

实际上从运动观点来看，在菱形ABCD中，显然有AC⊥BD，且分别平分四个内角。将△BCD沿着AB方向向右平移一定距离JB，AE，BE，CM，DM仍然分别是∠DAB，∠ABC，∠BCD，∠CDA的平分线，就可得到上述图形.由平移性质，可得DH=FN=JB=AB-AJ=AB-AD，又四边形EFMN是矩形，所以EM=FN=AB-AD此题是利用平移，追溯此图形的来龙去脉，了解运动的过程，证明简洁明了。

三、利用旋转变换来读图

旋转是指在平面内，把一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动称为旋转。这个定点叫做旋转中心，其性质为一是对应点到旋转中心的距离相等（意味着：旋转中心在对应点所连线段的垂直平分线上）。二是对应点与旋转中心所连线段的夹角等于旋转角。三是旋转前、后的图形全等。在图形中有全等图形且有公共点时，可考虑旋转变换来研究图形。这三种变换共同点是只改变图形的位置变化，而图形的大小没有发生变化。即和原来的图形是全等的。所以在遇到图形中有全等的图形可尝试通过观察、实践活动、动手操作等方式从变换的角度来读图。

另外图形问题中所涉及的元素大多较为分散，各个元素之间的关系不容易看出来。这时通过变换可将分散的元素集中在一起、将不规则图形变换为规则图形，将一般性质转换成特殊性质，这样就可分析问题中各元素之间的关系，研究图形在运动过程中的量化关系，并找出其规律，进而深入研究图形.

利用变换来读图，可使学生了解图形之间的关系.能够更好地解决问题，使学生感受和欣赏图形之美。有利于培养学生思维的灵活性和敏捷性、深刻性.有利于增强学生的创新性思维。

参考文献

[1]陈阿文.几何变换在初中几何解题中的应用[J].中学理科园地，2010（4）.

[2]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2011.