习题与变式
2017-07-08左效平
左效平
同学们若能对课本上的习题进行深入思考。往往能收到意想不到的效果。
在人教版七年级数学下册教科书中有如下一道习题(第70页第6题):
如图1,建立平面直角坐标系,能使点8,C的坐标分别为(0,0)和(4,0),写出点A,D,E,F,G的坐标,并指出它们所在的象限。
分析:要想求出点A,D,E,F,G的坐标,并指出它们所在的象限,正确建立平面直角坐标系是关键。而建立平面直角坐标系的核心要素是确定坐标原点的位置,找出水平的横轴和铅直的纵轴。
水平的横轴这样找:过坐标原点画一条水平的直线,规定向右为正方向。并且在直线上标上单位长度。
铅直的纵轴这样找:过坐标原点画一条与水平的横轴垂直的直线,规定向上为正方向,并且在直线上标上单位长度。
这样,平面直角坐标系就建立起来了。
在这里,要提醒同学们注意的是,当点在x轴或者y轴上时,不属于任何象限。
解:因为点B的坐标为(0,0),所以平面直角坐标系的原点是点B。因为点B,C的坐标分别为(0,0)和(4,0),所以点B,C在一条直线上,并且这条直线就是x轴所在的直线。过点B作直线BC的垂线,并且规定向上为正方向。这条垂线所在的直线就是y轴所在的直线,建立平面直角坐标系如图2所示。
所以点A(-2,3)位于第二象限,点D(6,1)位于第一象限,点E(5,3)位于第一象限,点F(3,2)位于第一象限,点G(1,5)位于第一象限。
变式1:两点坐标分别为(0,a)与(b,0),要求确定其他点的坐标。
要领:画出经过点(0,a)的铅直直线,画出经过点(b,0)的水平直线,建立平面直角坐标系,找出其他点的坐标。
例1 (2016年山西)如图3是利用网格画出的太原市地铁1号、2号线路部分规划示意图。若建立适当的平面直角坐标系。使“双塔西街”的坐标为(0,-1),“桃园路”的坐标为(-1,0),则“火车站”(正好在网格点上)的坐标是
。
分析:根据“双塔西街”的坐标为(0,-1),知道y轴是经过该点的铅直直线。且向上为正方向。根据“桃园路”的坐标为(-1,0),知道x轴是经过该点的水平直线。且向右为正方向。两线的交会处“大南门”为坐标原点。这样坐标系就建立起来了。解答就简单了。
解:“双塔西街”的坐标为(0,-1),“桃园路”的坐标为(-1,0),所以“大南門”为坐标原点,所以“火车站”(正好在网格点上)的坐标为(3,0)。
点译:确定坐标原点,确定数轴上单位长度是解题的关键。
变式2:两点坐标分别为(0,a)与(m,n),要求确定其他点的坐标。
要领:画出经过点(0,a)的铅直直线,画出经过点(m,0)的水平直线,建立平面直角坐标系,找出其他点的坐标。
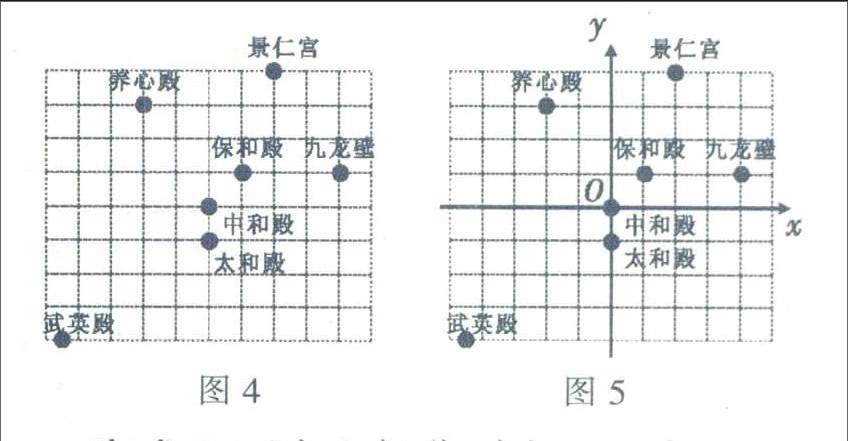
例2 (2015年北京)图4是利用平面直角坐标系画出的故宫博物院的主要建筑分布图。若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,太和殿的坐标为(0,-1),九龙壁的坐标为(4,1),则下列宫殿的坐标正确的是( )。
A.景仁宫(4,2) B.养心殿(-2,3)
C.保和殿(1,0) D.武英殿(-3。5,-4)
分析;根据太和殿的坐标为(0,-1),知道太和殿在y轴上。结合九龙壁的坐标为(4,1),可以确定坐标系的原点位于中和殿。建立如图5所示的平面直角坐标系。细心观察,景仁宫的坐标为(2,4),所以A是错误的。养心殿的坐标是(-2,3),所以B是正确的。保和殿的坐标是(1,1),所以C是错误的。武英殿的坐标是(-4。5,-4),所以D是错误的。
解:选B。
点评:平时多加练习,考试时才会得心应手。
变式3:两点坐标分别为(a,b)与(a,n),要求确定其他点的坐标。
要领:画出经过点(a,b),(a,n)的铅直直线,把直线向左或向右平移|a|个单位长度。得到),轴所在直线,画出经过点(a,0)的水平直线,建立平面直角坐标系,找出其他点的坐标。
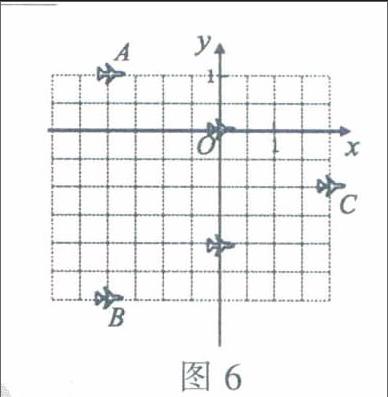
例3 (2015年绵阳)如图6是轰炸机的一个飞行队形,如果A,B两架轰炸机的坐标分别为(-2,1)和(-2,-3),那么轰炸机C的坐标是____。
分析:根据A(-2,1)和B(-2,-3),知道A,B两点在一条直线上,x轴位于点A下方且距点A一个单位长度,y轴位于点A右边且距点A两个单位长度,这样,我们就可顺利建立平面直角坐标系。
解:因为A(-2,1)和B(-2,-3),所以可得轰炸机C的坐标为(2,-1)。
点砰:根据A(-2,1)和B(-2,-3),确定原点的位置,建立平面直角坐标系是解题的关键。