引力场和静电场中几个重要定理的严格数学证明

沈进中， 邓留保

(1.安徽理工大学 电气与信息工程学院，安徽 淮南 232001；2.安徽财经大学 金融学院,安徽 蚌埠233030)



引力场和静电场中几个重要定理的严格数学证明

沈进中1， 邓留保2

(1.安徽理工大学 电气与信息工程学院，安徽 淮南 232001；2.安徽财经大学 金融学院,安徽 蚌埠233030)

物理学是理解各类实际模型的基础，深刻理解物理中的重要定理十分重要。从基本定义出发，采用多元积分的方法给出文献[1]中球壳定理的严格数学证明。进一步考虑均匀实心球体和两类带空腔球体的万有引力场分布，给出对应的严格数学证明。根据引力场与静电场的表达形式的相似之处，给出均匀带电球壳、实心球体和两类带空腔球体电场分布的数学表达式。

球壳定理；引力场；第二类曲面积分；静电场

笔者在研读专著[1]的过程中，遇到的第一个重要定理是引力的球壳定理(P320)，但它没有给出证明过程。陆续发现还有一些重要定理也没有给出数学证明，诸如球体引力场分布、电场中的球壳定理和球体定理，这对于物理定理的理解是不深刻的。许多文献往往是叙述而不证明，甚至都不陈述[2-3]。利用对称性和环带微元上的电场分布，文献[4-5]给出了球壳表面处的电场分布的证明。文献[6]采用对电容采用虚功原理求出球壳表面处的电场分布。本文从基本引力的定律和力的叠加原理出发，采用多重积分严格证明球壳、实心球体、带空腔球体的引力场分布公式。根据引力与静电力的数学表达式结构的相似性，可以很自然的给出电场中的球壳定理，进一步给出带空腔球体的电场分布，事实上，实心球体是空腔球体的特殊情形。相对于已存在的证明，本文给出证明从基本定义出发，因此更具“基础性、自然性”和严格性，对于理解球状几何体的引力场分布、电场分布、体会电场分布的对称性是大有益处的。

1 数学证明

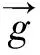
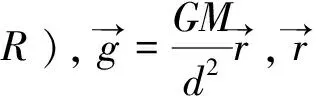
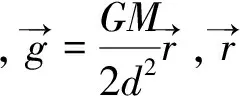
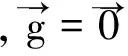
证明：如图1，建立空间直角坐标系，球心在原点O处。点p在z轴上。

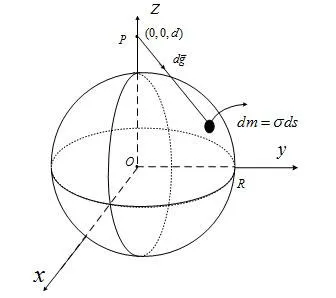
图1 空心球壳

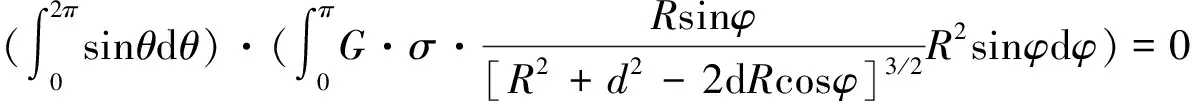
利用球的对称性，也可以直观得到gx=gy=0。

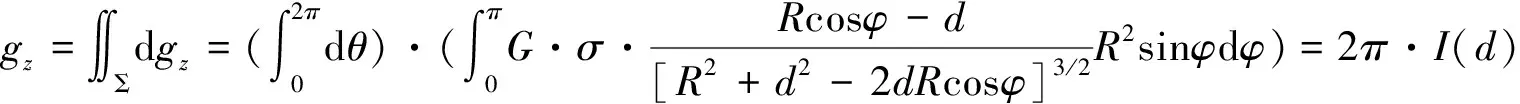
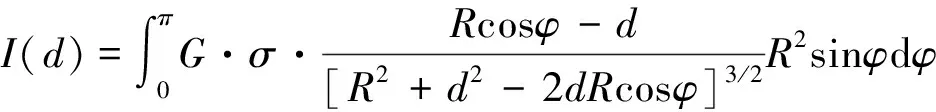
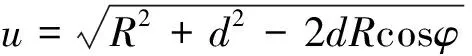
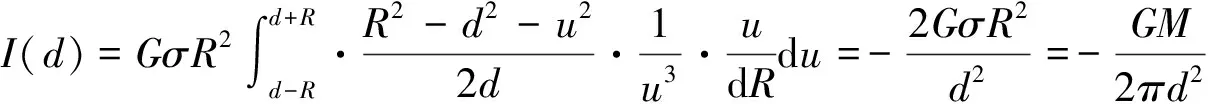
②当d=R，即点P在球壳上，

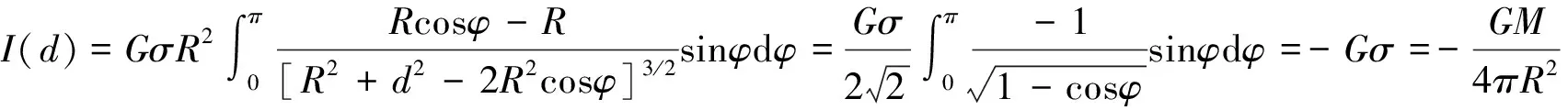
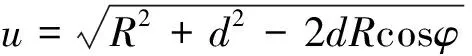
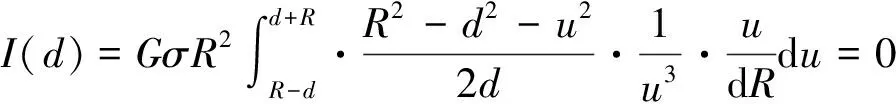
显然，这与所要证明的结论的含义是相同的。注意：这里的结论①③就是球壳定理的内容。

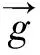
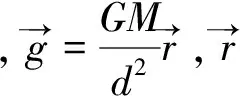
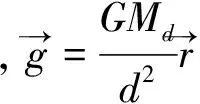
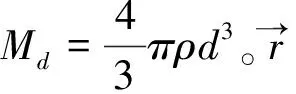
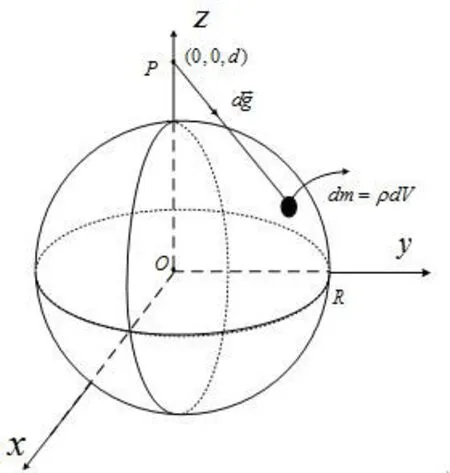
图2 实心球体

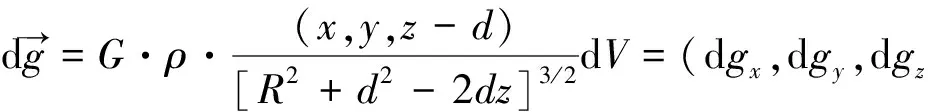
那么，

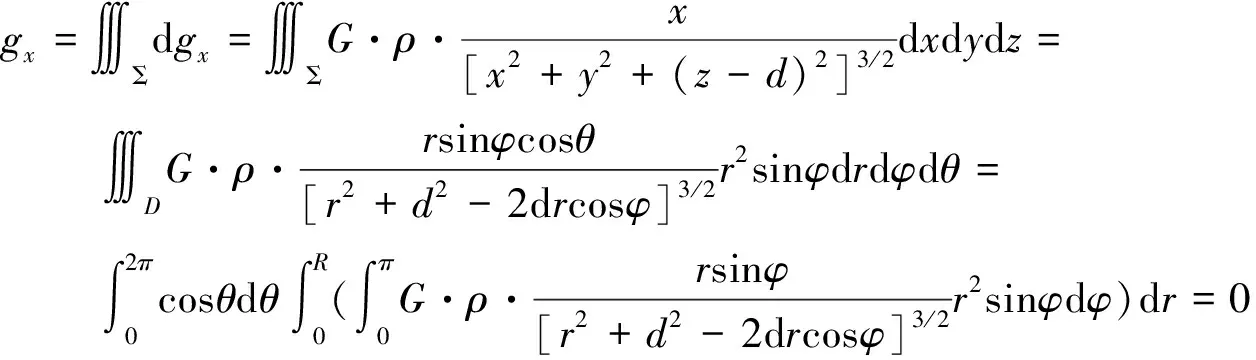
同理，可得

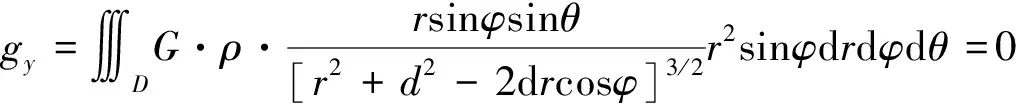
利用球的对称性，也可以直观得到gx=gy=0 。再来计算gz，

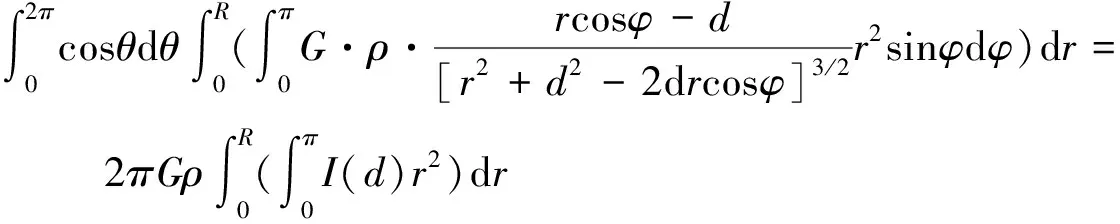
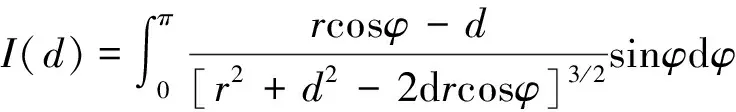
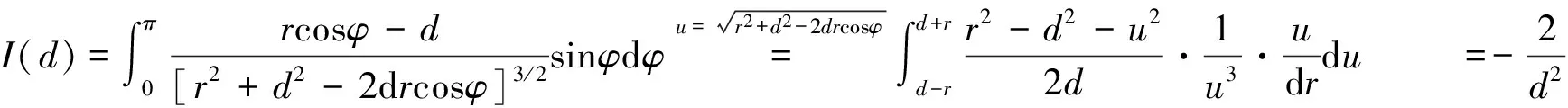
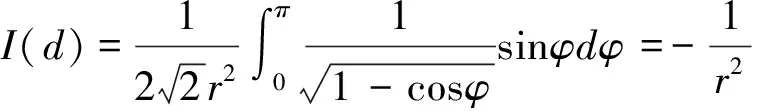
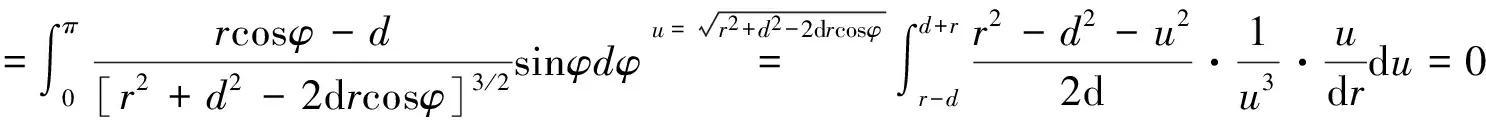
那么，可得gz为:

显然，这就是本定理的结论。注：专著[1]仅仅给出球壳定理(定理1)，并未给出涉及球体的相关结论。虽然在有关问题的处理上使用了定理2的结论，但仅仅是作为球壳定理的应用。严格地说这是不对的，因为球壳的质量分布是面分布，而不是体分布，二者不能类似看待。说的更严格一点，球壳是二维几何体，球体是三维几何体，可见球壳和球体是不同的。如果定理2中的球体带有空腔，那么它在空间中任意一点处的引力场又如何分布呢？对这个问题，我们给出以下两个定理。

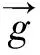
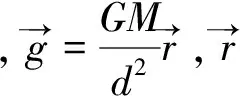
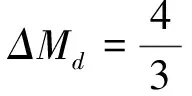
证明：

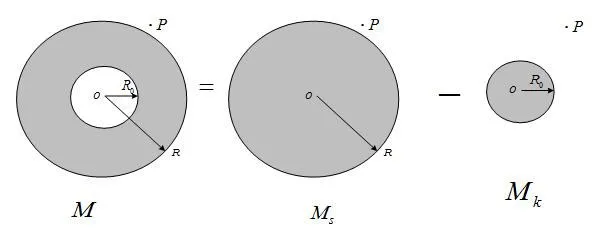
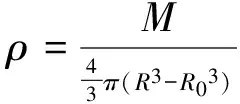
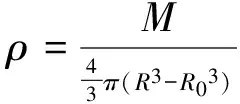
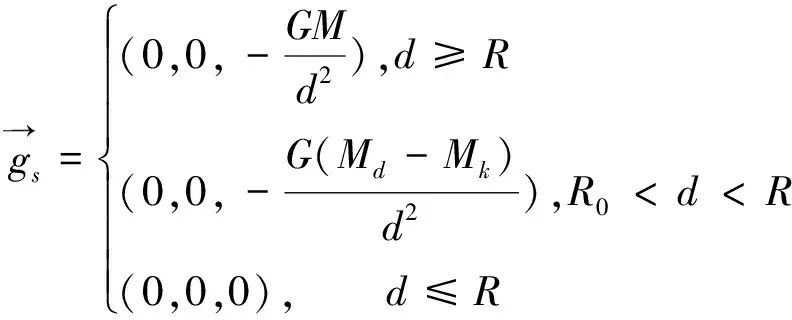
填满后的球形空腔部分在P处的引力场为：

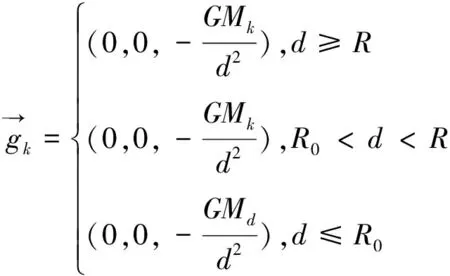
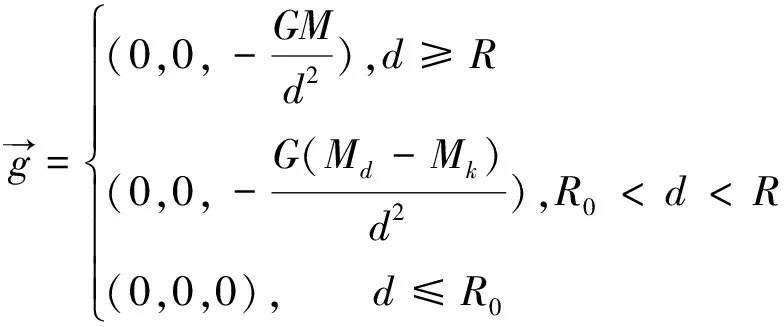
显然，这就是定理3所表达的物理含义，证毕。

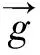
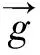
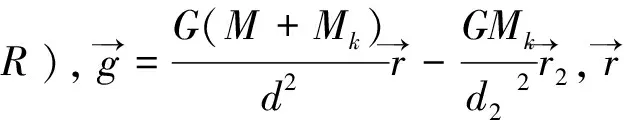
证明：将空腔中填满与原来球体相同的物质，使之成为一个实心球体。如图3，应用定理2的结论，采用证明定理3的处理方法，可以很容易得到定理4。这里仅对③做一点说明，由于

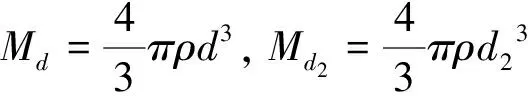
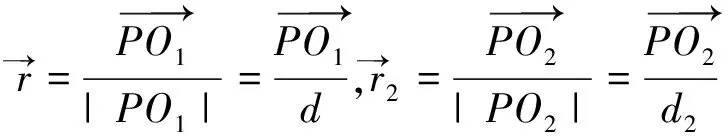
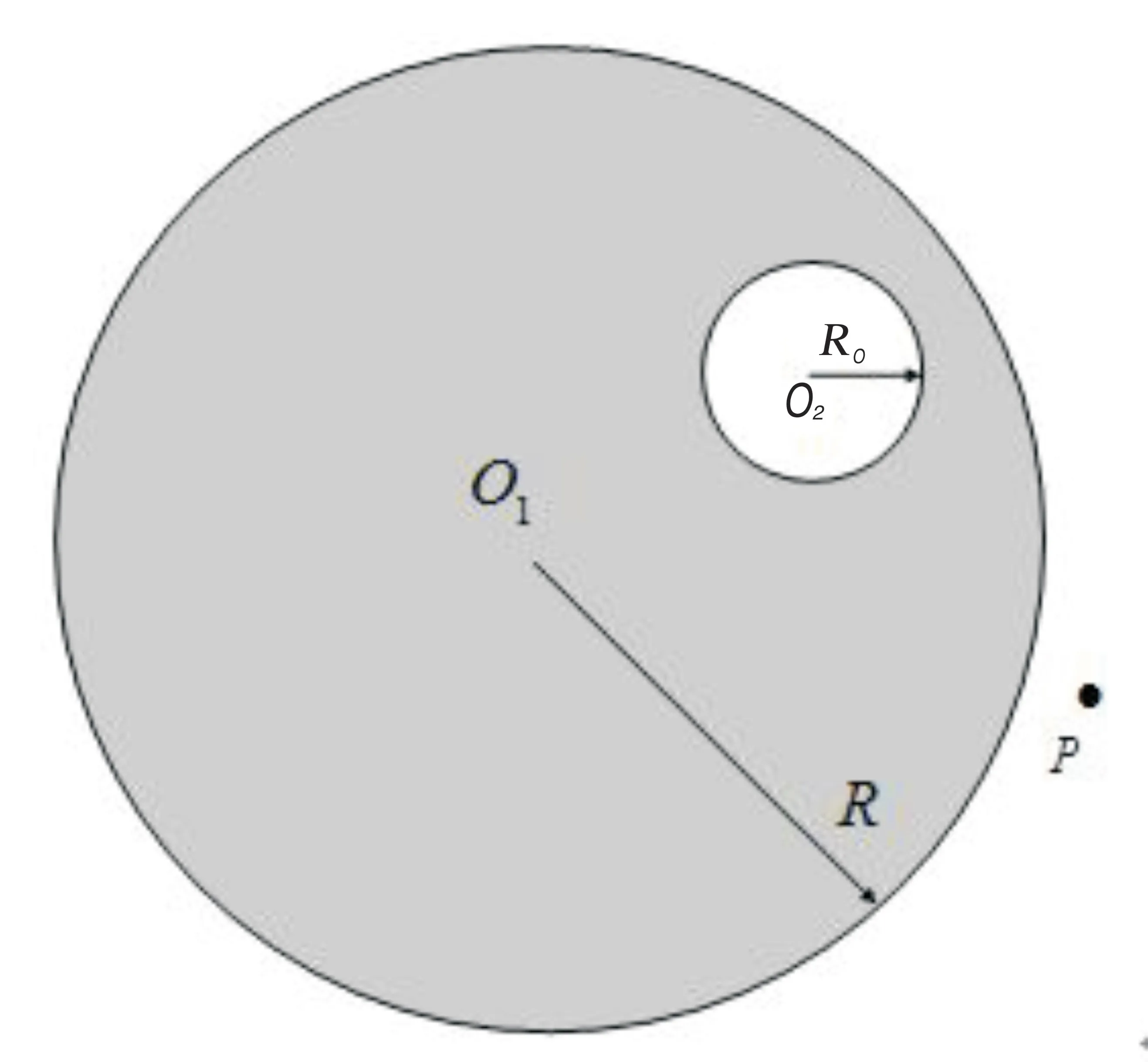
图3 含有空腔的球体

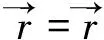
我们知道，一个质量为M的质点O在空间中任意一点P处产生的引力场为

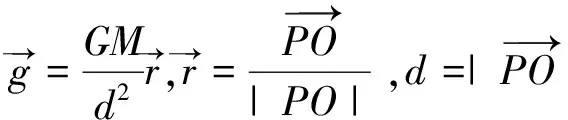
注：一个带电量为+q的质点O在空间中任意一点P处产生的静电场为

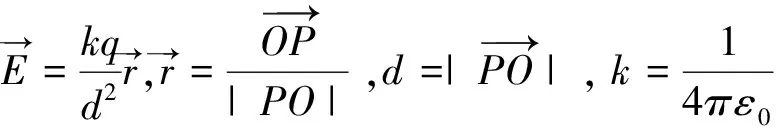
改写一下，可得

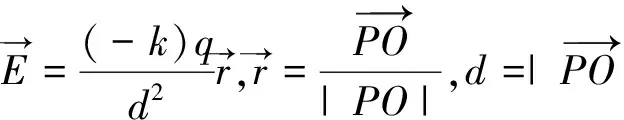
因此，无需重新推导，只需将质量符号改成电荷符号，采用完全相同的证明过程就可得到均匀带电球壳和带空腔的均匀带电球体的电场分布，下面以定理的形式给出相应的结论。

定理5 有一带电量为+q，半径为R、球心为O的均匀球壳，对空间中一点P，点P到O的距离为d。那么此带电球壳在P处产生的静电场为:

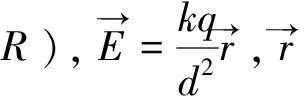
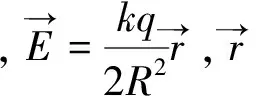
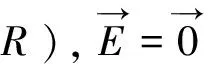
定理6 有一带电量为+q，半径为R、球心为O1的均匀(电荷体密度为σ)球体，其内部含有一个球心为O2球形空腔，空间中一点P，点P到O的距离为d。那么此带电球壳在P处产生的静电场为：

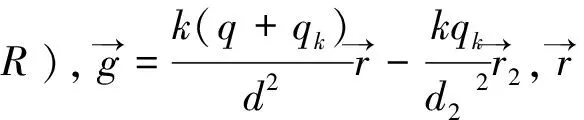
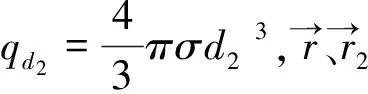
2 结语

主要考虑球壳和球体的引力场分布，作为类比，也给出了均匀带电球壳和球体的静电场分布。目的主要是补充文献[1]中球壳定理的完整的严格证明。进一步，还给出球体的引力场、带空腔的球体的引力场的空间分布数学表达式，并给出相应的完整数学证明。由于静电场的库仑定律与万有引力在形式上相同，因而可以不费笔墨很容易得到对应的结论。至于证明，只需将相应的符号替换，其证明过程完全相同。

[1]HALLIDAYD,RESNICKR,WALKERJ.物理学基础[M].6版.张三慧,李椿，滕小瑛，译.北京:机械工业出版社,2005:320-325.

[2] 郑永令,贾起民,方小敏.力学[M].北京:高等教育出版社,2002:65-68.

[3] 贾起民,郑永令,陈暨耀.电磁学[M].2版.北京:高等教育出版社,2001:11-21.

[4] 彭海鹰.均匀带电球面的电场强度分布再讨论[J].物理与工程,2003,13(1):60-61.

[5] 牛庆林,王晓丽.均匀带电球面电场强度的再讨论[J].临沂大学学报,2016,38(1)：142-144.

[6] 刘景世.“均匀带电球面上的电场强度如何计算”的再讨论[J].河南教育学院学报(自然科学版),2011,20(1)：32-33.

Mathematical Proof of Several Important Theorems in Gravitational Field and Electric Field

SHEN Jinzhong1, DENG Liubao2

(1.College of Electrical and Information Engineering,Anhui University of Science and Technology,Huainan Anhui 232001,China；2. School of Finance,Anhui University of Financial and Economics,Bengbu Anhui 233030,China)

Physics is the basis of understanding all kinds of practical models, therefore, a deep understanding of important theorems in physics is very important. The strict mathematical proof of Shell theorem in literature [1] is gave by applying the multiple integral method and basic definitions. Further,consider gravitational field distribution of the uniform solid sphere and two kinds of hollow spheres, and give the corresponding strict mathematical proof. Based on that the expression forms of gravitational field and electrostatic field are similar, mathematical expressions of electric field distribution are given for the uniformly charged spherical shell, a solid sphere and two kinds of hollow spheres.

Shell theorem; gravitational field; second-type surface integral; electric field

2016-10-17

安徽理工大学硕博基金(ZY022)；安徽高校自然科学研究重点项目(KJ2015A076)

沈进中(1985-)，男，讲师，博士，主要从事电力控制，场论和非线性系统教学与研究。E-mail:jzshen009@163.com

O412.3

A

1004-2237(2017)03-0058-07

10.3969/j.issn.1004-2237.2017.03.012