一种特殊补图的最小特征值研究

李 雨，薛婷婷，孙 威，王振东，黄 星

(安庆师范大学，安徽 安庆 246133)



一种特殊补图的最小特征值研究

李 雨，薛婷婷，孙 威，王振东，黄 星*

(安庆师范大学，安徽 安庆 246133)

图的邻接矩阵是表示顶点之间相邻关系的矩阵,它的最小特征值就是图的最小特征值。讨论特殊补图的最小特征值,并刻画此类图最小特征值达极小的唯一图，也是有意义的。

图论；邻接矩阵；补图；最小特征值

设G=(V,E)是一个顶点集为V={v1,v2,…,vn}和边集为E={e1,e2,…,en}的n阶简单图,顶点v∈V的邻域定义为NG(v)={u∶uv∈E},顶点v∈V的度定义为d(v)=|NG(v)|。若|NG(v)|=1，则称v为G的悬挂点。如果图G中任意两点间均有一条路连接，则称G是连通的。图G的邻接矩阵定义为A(G)=(aij)n×n，其中，当vi与vj相邻时，aij=1，否则aij=0。A(G)的特征值被称为图G的特征值。由于A(G)是实对称矩阵，故其特征值为实数，可以进行排序，我们称A(G)的最小特征值为图G的最小特征值，记为λmin(G)。

邻接谱半径的极图问题是谱图理论的热点问题。然而,相对于谱半径,最小特征值研究很少被人注意到。2008年，Bell在文献[1,2]中刻画了某些图类的最小特征值的极小图。他的工作使得图的最小特征值问题受到国内外学者的注意，具体可参阅文献[3-15]。特别是文献[11-15]，都是从补图的结构出发，研究了原图的最小特征值。本文仍然从补图的角度出发研究给定阶数的特殊补图的最小特征值，并刻画此类图最小特征值达极小的唯一图。

下面我们引进一些定义。设G=(V,E)为n阶简单图,对于向量X∈Rn,如果存在一个从V到X中值的映射φ,使得对于任意u∈V有Xu=φ(u),则称X定义在G上。

我们发现对于任意向量X∈Rn，有

(1)

若λ是A(G)对应于特征向量X的特征值,则由特征值的定义,当且仅当X≠0,对于每个v∈V,有

(2)

我们称等式(2)为G关于X的特征等式。另外,对于任意单位向量X∈Rn,有

λmin(G)≤XTA(G)X

(3)

当且仅当X是G的第一特征向量时等式成立。

Gc表示图G的补图。显然有A(Gc)=J-I-A(G),其中J,I分别表示n阶全1矩阵和单位矩阵。因此,对于任意向量X∈Rn,有

XTA(Gc)X=XT(J-I)X-XTA(G)X

(4)

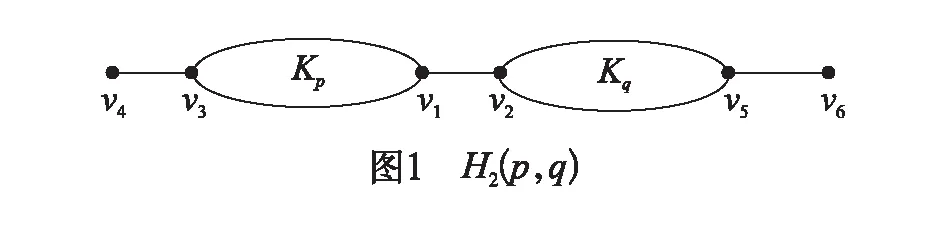
记H2(p,q)(如图1所示)是阶为p+q+2(p≥1,q≥1)的特殊图，它是由两个不相交的完全图Kp,Kq以及两个孤立点v4,v6通过以Kp的一个顶点v1与Kq的一个顶点v2为端点的边v1v2和Kp,Kq各一个顶点v3,v5与两个孤立点v4,v6为端点的边v3v4，v5v6连接的图。特别地，当q=1时,v2=v5；当p=1时,v1=v3。

引理1[16]设A是一个实对称n×n阶矩阵,B为A的m×m阶主子阵,且λ1(A)≥λ2(A)≥…≥λn(A),λ1(B)≥λ2(B)≥…≥λm(B)分别为A与B的特征值,则对于i=1,2,…,m,有λn-m+i(A)≤λi(B)≤λi(A)。

定理2 给定一个正整数n(n≥11),对于任意的整数p≥1,q≥1且p+q=n-2,我们有λmin(H2(p,q)c)≥λmin(H2([n-2/2],[n-2/2])c),当且仅当p=[n-2/2],q=[n-2/2]时等号成立。

证明 设H2(p,q)如图1所示,由于K2⊂H2(p,q)c,λmin(k2)=-1。由引理1可知

λmin(H2(q,p)c)≤-1

(5)

设X是H2(p,q)c的第一特征向量。

情形1：当p=1时。由等式(2)与(5)知Kq中除v2,v5两点外所有的点在X中对应的值相同，记为X1。记Xv1(v3)=X2,Xv2=X3,Xv4=X4Xv5=X5,Xv6=X6,记λmin(H2(1,n-3)c)=λ，这样由等式(2)可以得到,

将上式转换成矩阵等式(B-λI)X′=0,其中X′=(X1,X2,X3,X4,X5,X6)T,

令

f1(x)=det(B-xI)=x6-x4(3n-9)-x3(4n-18)+x2(4n-16)+2x(n-5)-(n-5)。

情形2：当q=1时。由等式(2)与(5)知Kp中除v1,v3两点外所有的点在X中对应的值相同,记为X1。记Xv1=X2,Xv2(v5)=X3,Xv3=X4,Xv4=X5,Xv6=X6,记λmin(H2(n-3,1)c)=λ,再由等式(2)可以得到,

将上式转换成矩阵等式(B-λI)X′=0,其中X′=(X1,X2,X3,X4,X5,X6)T,

令

f2(x)=det(B-xI)=x6-x4(3n-9)-x3(4n-18)+x2(4n-16)+2x(n-5)-(n-5)。

情形3：当p,q≥2时。由等式(2)与(5)可知Kp中除v1,v3点外所有的点在X中对应的值相同,记为X1,在Kq中除v2,v5两点外所有的点在X中对应的值相同,记为X4记Xv1=X2,Xv2=X3,Xv3=X5,Xv4=X6,Xv5=X7,Xv6=X8,λmin(H2(p,q)c)=λ,这样由等式(2)可以知,

将上式转换成矩阵等式(B-λI)X=0,其中X′=(X1,X2,X3,X4,X5,X6,X7,X8)T,

令

f(x；p,q)=det(B-xI)=x8-x6(pq+2n-6)-x5(4pq-8)+x4(4n-15)+x3(8pq-8n+20)-x2(3n-17)-4x(pq-2n+8)+(pq-2n+8)。

由于2≤x≤n-4时，φ(x)=x(n-2-x)取最小值φ(2)=2(n-4)，故当p,q≥2,p+q=n-2时，pq=p(n-2-p)≥2(n-4)。则当p,q≥2且p+q=n-2≥9时，f(-4;p,q)=77208-6738n-495pq<0，从而有λ<-4。

(1)若p≥q+2,当x<-4时，我们有

f(x;p,q)-f(x,p-1,q+1)=(p-q-1)(x6+4x5-8x3+4x-1)>0。

由于λ是方程f(x;p,q)的最小根,从而有f(λ;p,q)=0,这样由上式可得到f(λ;p-1,q+1)<0,这意味着

λmin(H2(p,q)c)>λmin(H2(p-1,q+1)c)>…>λmin(H2([n-2/2],[n-2/2])c)。

(2)若q≥p+1,当x<-4时，且q≥p+2时，我们有

f(x;p,q)-f(x;p+1,q-1)=(q-p-1)(x6+4x5-8x3+4x-1)>0。

当x<-8时，且q=p+1时，我们有

f(x;p,q)-f(x;p+1,q-1)=0。

由于λ是方程f(x;p,q)的最小根,从而有f(λ;p,q)=0,则由上面的讨论知当q≥p+1时，我们有f(λ;p+1,q-1)≤0,这意味着

λmin(H2(p,q)c)≥λmin(H2(p+1,q-1)c)≥…≥λmin(H2([n-2/2],[n-2/2])c)。

下面比较λmin(H2(n-4,2)c)与λmin(H2(n-3,1)c)的大小。

因为n≥11且x<-4，有x2f2(x)-f(x;n-4,2)=x6(n-5)+x5(4n-22)-x4-x3(6n-34)+x2(2n-12)>x6(n-5)+x5(4n-22)-x4=φ(x)关于x单调递减，故有x2f3(x)-f(x;n-4,2)>φ(-4)=7x4>0。因为λmin(H2(n-4,2)c)<-4，我们有λmin(H2(n-4,2)c)<λmin(H2(n-3,1)c)。

再综合情形1、2、3知结论成立。

[4] Y.Z.Fan,Y.Wang,Y.B.Gao.Minimizing the least eigenvalues of unicyclic graphs with application to spectral spread[J].Linear Algebra Appl,2008，429(2-3):577-588.

[5] R. Liu,M.Zhai,J.Shu.The least eigenvalues of unicyclic graph with n vertices and k pendant vertices[J].Linear Algebra Appl,2009，431(5-7):657-665.

[7] Y.Y.Tan,Y.Z.Fan.The vertex(edge) independence number,vertex(edge) cover number and the least eigenvalue of a graph[J].Linear Algebra Appl,2010，433(4):790-795.

[8] Y.Wang,Y.Z.Fan.The least eigenvalue of a graph with cut vertices[J].Linear Algebra Appl,2010，433(1):19-27.

[9] M.L.Ye,Y.Z.Fan,D.Liang.The least eigenvalue of graphs with given connectivity[J].Linear Algebra Appl,2009，430(4):1375-1379.

[10] G.D.Yu,Y.Z.Fan,Y.Wang.Quadratic forms on graphs with application to minimizing the least eigenvalue of signless Laplacian over bicyclic graphs[J].Electronic Journal of Linear Algebra,2014,27:213-236.

[11] Y.Z.Fan,F.F Zhang,Y.Wang.The least eigenvalue of the complements of tree[J].Linear Algebra Appl,2011，435(9):2150-2155.

[12] S.C.Li, S.J.Wang.The least eigenvalue of the signless Laplacian of the complements of trees[J].Linear Algebra Appl,2012，436(7):2398-2405.

[13] Y.Wang,Y.Z.Fan,X.X.Li,et al.The least eigenvalue of graphs whose complements are unicyclic[J].Discussiones Mathematicae Graph Theory,2013，35(2):1375-1379.

[14] G.D.Yu,Y.Z.Fan,Y.Wang.The least eigenvalue of graphs[J].Journal of mathematical research with application,2012，32(6):556-561.

[15] G.D.Yu,Y.Z.Fan.The least eigenvalue of graphs whose complements are 2-vertex or 2-edge connected[J].Operations Research Transactions,2013，17(2):81-88.

[16] W.haemers. Interlacing eigenvalues and graphs[J].Linear Algebra Appl,1995，226-228(95):593-616.

Study on the Minimum Eigenvalue of A Special Complement Graph

LIYu,XUETing-ting,SUNWei,WANGZhen-dong,HUANGXing

(AnqingNormalUniversity,Anqing246133,China)

The adjacency matrix is a matrix representation of adjacent relation between the vertex and the smallest eigenvalue is the minimum feature value. This paper discusses the special characteristics of complementary graph, and describes a special graph of this kind when the minimum eigenvalue reaches the minimum. The paper is of importance to future studies.

graph theory; adjacency matrix; complement graph; minimum eigenvalue

2017-04-12

国家自然科学基金资助项目(11604002，51607004)

李雨(1992-)，女，安庆师范大学计算机与信息学院在读硕士研究生，研究方向：数据挖掘、文本分类。

黄星(1989-)，男，博士，安庆师范大学物理与电气工程学院讲师，研究方向：图论与图像处理。

O157.5

A

1674-3229(2017)02-0005-03