一类基于病毒治疗的时滞HIV-1模型
2017-07-05刘娟
刘 娟
(蚌埠学院,安徽 蚌埠 233030)
一类基于病毒治疗的时滞HIV-1模型
刘 娟
(蚌埠学院,安徽 蚌埠 233030)
研究一类具有标准发生率的利用病毒治疗时滞HIV感染的传染病模型。以细胞内作用延迟时滞为分支参数,利用特征值方法,通过分析模型线性部分特征方程根的分布情况,讨论模型正平衡点的局部渐近稳定性,确定模型产生局部Hopf分支的时滞临界点,给出模型局部渐近稳定和产生局部Hopf分岔的充分性条件。最后,利用仿真示例,验证所得结果的正确性。仿真结果表明,当细胞内作用延迟足够小时,病毒数量将会得到控制。
Hopf分岔;HIV-1模型;时滞;稳定性
0 引言
流行病学中的数学建模为理解疾病的传播机制,有效控制疾病的传播提供了有效策略。人类免疫缺陷病毒(HIV)是一种可以引起获得性免疫缺陷综合征的慢性病毒,严重威胁着人类的健康和社会发展[1,2]。因此,多年以来,国内外研究学者先后提出了多种HIV病毒模型并对其传播规律进行深入研究[3-5]。尤其文献[6]提出了一类具有标准发生率的基于病毒治疗的HIV-1动力学模型:
(1)
其中,x(t),y(t),v(t),z(t),w(t)分别表示未感染宿主细胞,受感染的细胞,病原病毒,重组感染的细胞以及重组病毒在时刻t的数量;η是正常细胞的生产率,d是正常细胞的死亡率,α是受病毒感染细胞重组的速率,β是常细胞的感染率,a是受感染细胞的死亡率,k是受感染细胞产生病原体的速率,u是病原体的死亡率,q是重组病毒的死亡率,b是双病毒感染细胞的死亡率,c是双病毒感染细胞产生重组病毒的速率。文献[6]利用Routh-Hurwitz准则以及扰动引理,证明了模型(1)无病平衡点的全局稳定性。
显然,模型(1)忽略了细胞内作用延迟所引起的时滞因素。时滞对动力学模型的稳定性有着非常重要的影响。比如,时滞可以导致模型稳定性的变化,使得模型从稳定变得不稳定,从而引起模型的Hopf分岔以及周期现象[7]。在实际的疾病传播过程中,周期现象很不利于疾病的传播控制。基于此并考虑到细胞内的作用延迟,本文在模型(1)中引入细胞内作用延迟所引起的时滞因素,研究如下具有时滞的HIV动力学模型:
(2)
其中,τ为细胞内作用延迟所引起的时滞。
1 Hopf分岔的存在性
根据文献[6]的分析结果可知,当

x*=
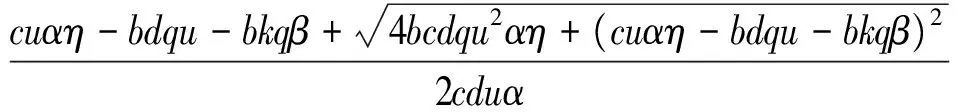
模型(2)在正平衡点E*(x*,y*,z*,v*,w*)处线性化部分的特征方程为:
λ5+m4λ4+m3λ3+m2λ2+m1λ+m0
+(n4λ4+n3λ3+n2λ2+n1λ+n0)e-λτ
+(p3λ3+p2λ2+p1λ+p0)e-2λτ=0
(3)
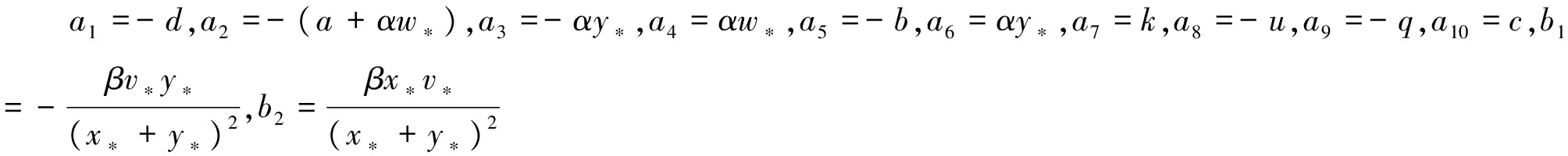
方程(3)左右两边同时乘以eλτ,
n4λ4+n3λ3+n2λ2+n1λ+n0
+(λ5+m4λ4+m3λ3+m2λ2+m1λ+m0)eλτ
+(p3λ3+p2λ2+p1λ+p0)e-λτ=0
(4)
当τ=0时,方程(3)变为
λ5+m04λ4+m03λ3+m02λ2+m01λ+m00=0
(5)
其中,
m00=m0+n0+p0,m01=m1+n1+p1,
m02=m2+n2+p2,m03=m3+n3+p3,m04=m4+n4。
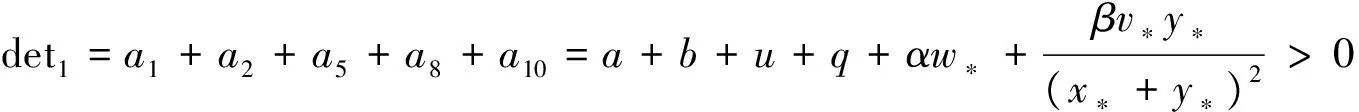
(6)
(7)
(8)
(9)
当τ>0时,令λ=iω(ω>0)为方程(4)的根,则
其中,
g1(ω)=m4ω4-(m2+p2)ω2+m0+p0,
g2(ω)=m5-(m3-p3)ω3-(m1-p1)ω,
g3(ω)=n2ω2-n4ω4-n0,
g4(ω)=m4ω4-(m2-p2)ω2+m0-p0,
g5(ω)=ω5-(m3+p3)ω3-(m1+p1)ω,
g6(ω)=n3ω3-n1ω。
进而,
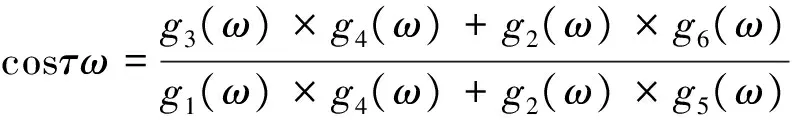
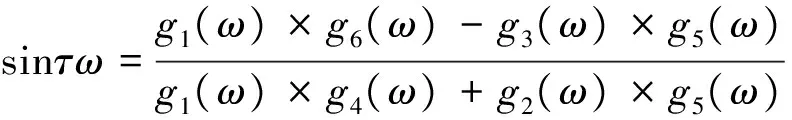
于是得到关于ω的下列方程,
cos2τω+sin2τω=1
(10)
为了给出本文主要结果,我们给出如下假设。
(H2)方程(10)至少存在一个正实根ω0。
对于ω0,有
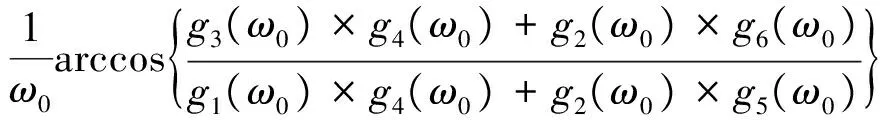
将λ(τ)代入方程(5)并在方程(5)左右两边求λ关于τ的导数,得到,

其中,
H1(λ)=4n4λ3+3n3λ2+2n2λ+n1+(3p3λ2+2p2λ+p1)e-λτ+(5λ4+4m4λ3+3m3λ2+2m2λ+m1)eλτ,
H2(λ)=λ(λ5+m4λ4+m3λ3+m2λ2+m1λ+m0)eλτ-λ(p3λ3+p2λ2+p1λ+p0)e-λτ。
令,
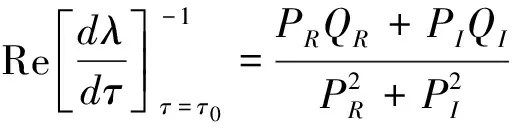
因此,如果条件(H2),即PRQR+PIQI≠0成立。则产生Hopf分岔的横截性条件满足。根据文献[8]中的Hopf分支存在定理,可以得到下列结果。
定理1 对于模型(2),如果条件(H1)、(H2)成立,那么当τ∈[0,τ0)时,正平衡点E*(x*,y*,z*,v*,w*),局部渐近稳定;当τ=τ0时模型(2)产生局部Hopf分岔并在正平衡点E*(x*,y*,z*,v*,w*)处产生局部Hopf分支。
2 仿真示例
选取文献[6]中的一组参数:η=2,β=0.5,d=0.01,a=0.33,α=0.004,b=2,k=50,u=2,c=2000,q=2。得到模型(2)的下列示例:
(11)
经过直接计算得到,
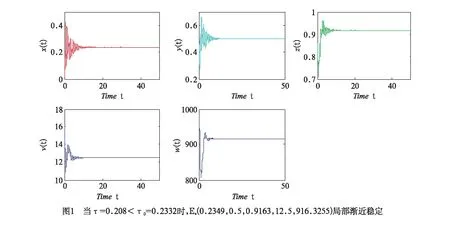
=18.5014>0。进而得到示例系统(11)的正平衡点E*(0.2349,0.5,0.9163,12.5,916.3255),进而得到ω0=1.9902,τ0=0.2332。根据定理1,当τ<τ0=0.2332时,正平衡点E*(0.2349,0.5,0.9163,12.5,916.3255)是局部渐近稳定的,仿真如图1所示。而当τ>τ0=0.2332时,正平衡点E*(0.2349,0.5,0.9163,12.5,916.3255)失去稳定,并产生局部Hopf分支。仿真效果如图2所示。
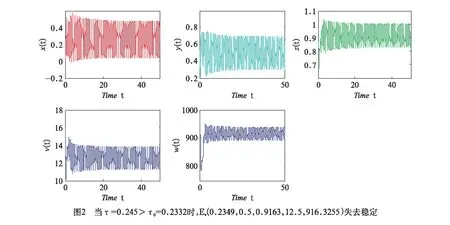
3 结论
本文在文献[6]的基础上,考虑到细胞内作用延迟,研究了一类具有标准发生率的时滞HIV-1病毒动力学模型。并以时滞为分支参数,研究了模型的局部渐近稳定性和局部Hopf分支的存在性。仿真结果表明,在一定条件下,如果时滞取值足够小时,病毒的传播趋于渐近稳定,容易得到控制。当时滞取值超过时滞关键值时,病毒的传播失去控制。因此,可以通过严格控制细胞内作用延迟时间以达到对病毒的控制。和文献[6]相比,本文主要研究了细胞内作用延迟引起的时滞因素对模型的影响。
[1] 刘永奇,熊建栋.一类具有Beddington-DeAngelis功能性反应的时滞HIV模型全局性分析[J].河南师范大学学报(自然科学版),2016,44(4):14-20.
[2] Nolan G P.Harnessing viral devices as pharmaceuticals: fighting HIV-1′s fire with fire[J].Cell,1997,90(5):821-824.
[3] Revilla T,Garcia-Ramos G. Fighting a virus with a virus: a dynamic model for HIV-1 therapy[J].Mathematical Biosciences, 2003,185(2):191-203.
[4] Ali N,Zaman G, Algahtani O. Stability analysis of HIV-1model with multiple delays[J].Advances in Difference Equations,2016,(88):1-12.
[5] 韩溢,杨志春.具有时滞和非线性感染率的HIV模型的稳定性和持续性[J].西南大学学报(自然科学版),2013,35(3):84-90.
[6] 庄科俊.一类基于病毒治疗的HIV-1动力学模型[J].生物数学学报,2015,30(2):372-376.
[7] Zhang J F.Bifurcation analysis of a modified Holling-Tanner predator-prey model with time delay [J].Applied Mathematical Modelling, 2012,36(3):1219-1231.
[8] Hassard B.D,Kazarinoff N.D,Wan Y.H.Theory and Applications of Hopf Bifurcation[M].Cambridge:Cambridge University Press,1981.
A Delayed HIV-1 Model of Fighting a Virus with Another Virus
LIUJuan
(BengbuUniversity,Bengbu233030,China)
A delayed HIV-1 model of fighting a virus with another virus and standard incidence rate is proposed in the present paper. Local stability of the positive equilibrium is investigated by regarding the intracellular delay as a bifurcation parameter. Critical value of the delay at which a Hopf bifurcation occurs is determined using characteristic value method and analyzing distribution of roots of the characteristic equation. Finally, numerical simulations are carried out in order to verify the obtained results. It has shown that the virus may be controlled when the value of the intracellular delay is small enough.
Hopf bifurcation; HIV-1 model; delay; stability
2017-03-07
2015年度安徽省高等学校省级自然科学研究项目(KJ2015A144)
刘娟(1979-),女,硕士,蚌埠学院理学院副教授,研究方向:微分方程、生物数学。
O175.12
A
1674-3229(2017)02-0008-05
