例析多角度寻找三角求值问题的解题突破口

江苏省海门中学 (226100) 曹亚东

例析多角度寻找三角求值问题的解题突破口

江苏省海门中学 (226100) 曹亚东

在我们的平常教学中经常碰到学生问这样的问题:“老师，三角函数公式多它的变换也非常多，请您教教我们如何寻找三角求值问题的解题突破口”.本文以一道习题为例，谈谈我是如何让学生寻找到解题突破口的.

习题 已知函数f(x)=sinx+2cosx，若函数g(x)=f(x)-m在x∈(0,π)上有两个不同零点α、β，则cos(α+β)= .

一、从变换角入手寻找解题突破口

观察方程sinx+2cosx-m=0它有常数m，能否从消去m入手呢？将两方程

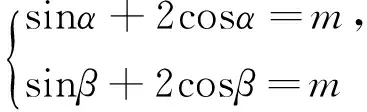
解法一：g(x)在x∈(0,π)上有两个不同零点α、β，∴sinα+2cosα=m，sinβ+2cosβ=m,两式相减得sinα-sinβ+2(cosα-cosβ)=0,

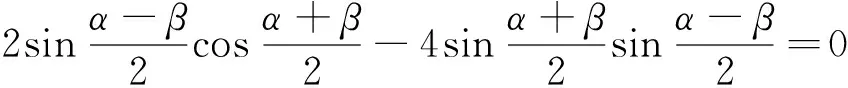
利用角的变换的关键在于尽量向特殊角或可计算角转化.如果题中有较多的相异角，这时就要根据角与角之间的和差、倍角、互补、互余的关系进行变角，从而使问题获解.

二、从变换三角函数名称入手寻找解题突破口

要使方程g(x)=0如何在x∈(0,π)上有两个不同的解α、β，我们能否构造出一个一元二次方程呢？观察方程sinx+2cosx=m，我们首先想到将方程两边平方，由韦达定理得到cosαcosβ以及sinαsinβ，从而求出cos(α+β)的值.

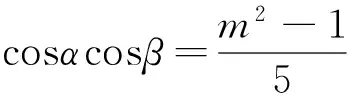
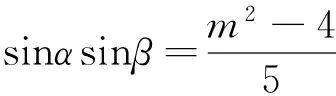
假如我们不平方，能否也能得到一个一元二次方程呢？对于正余弦只能缩角才能升次，这就想到了万能公式的应用.

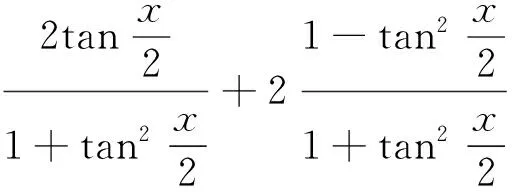
变函数名就是把一个等式尽量化成同一名称或相近的名称，可以把所有的切都转化为相应的弦，或把所有的弦转化为相应的切来求解.

三、从结构式入手寻找解题突破口

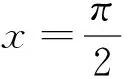
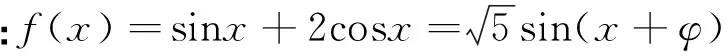
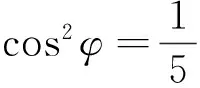
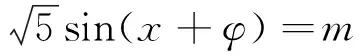
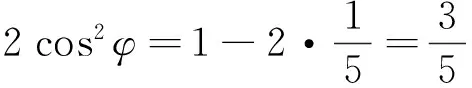
从结构式入手，关键在于题设中给出的信息要和我们学过的公式定理等等沟通起来，不然就不能运用结构寻找到解题突破口.一般题目中往往有明显的结构特征时，就暗示我们要从结构上面来突破.

四、从数形结合的角度寻找解题突破口

数形结合是一种重要的解题途径.把已知的数式等与图像的几何意义结合起来，然后将数和形巧妙的结合起来，从而快速地寻找到解题突破口.观察方程sinx+2cosx-m=0，能否从形的角度入手呢？

这就要求我们要能从方程看出它的几何意义.把点(cosx,sinx)看成是直线2x+y-m=0与单位圆x2+y2=1的交点来求解.

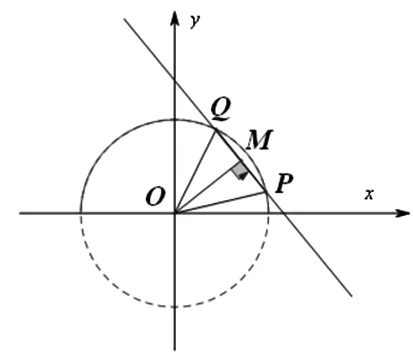
图1

解法五：设P(cosx,sinx)，则sinx+2cosx-m=0在x∈(0,π)上有两个不同零点α、β等价于直线l:2x+y-m=0与单位圆x2+y2=1(y>0)的上半圆有两个交点P,Q，如图1所示.

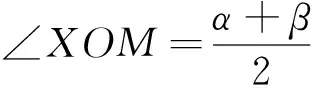
数形结合解题非常好，但对学生的要求比较高，它需要我们的学生牢固掌握一些概念和运算的几何意义，以及曲线的代数特征，然后利用题目中的条件和结论等分析它的几何意义，通过设参数达到数向形的转化.

上面介绍了四种寻找解题突破口的常用方法，实际上数学解题的突破口远远不止这四种方法，在我们平时解题过程中多注意思想方法的积累并将它灵活运用.只有让我们的学生牢固掌握数学的基本概念基本方法和基本定理，根据具体问题具体分析，凭借积累的经验、直觉和灵感等不断尝试探索，从而快速而准确地找寻到具体而恰当的解题方法，这才是学好数学之关键所在.