多角度探究一道试题的一般情形*

北京市第十二中学高中部 (100071) 刘 刚 赵 毅

多角度探究一道试题的一般情形*

北京市第十二中学高中部 (100071) 刘 刚 赵 毅

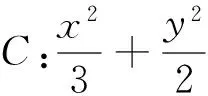
(1)求证：直线PA与PB的斜率乘积为定值；

(2)设点M，N在椭圆C上，O为坐标原点，当OM∥PA，ON∥PB时，求ΔOMN的面积．

试题考查了椭圆的标准方程、直线与椭圆的位置关系、椭圆直径的一个性质及以椭圆一组共轭直径为背景的三角形面积问题，考查了坐标法的应用．经过对(2)问的一般化探究，可以得到下面的结论．

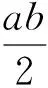
分析1:以MN为底，点O到直线MN的距离为高进行求解．

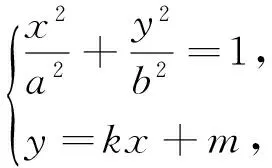
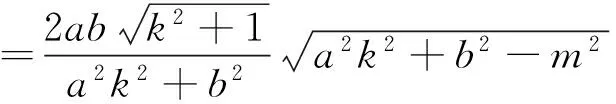
分析2:利用“水平底，铅锤高”表示三角形的面积，并借助椭圆的参数方程进行求解．

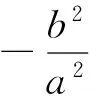
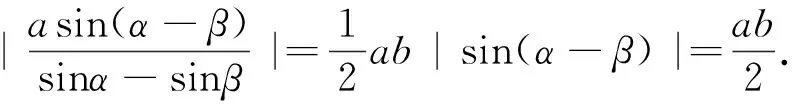
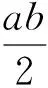
分析3:利用直线OM，ON的方程进行求解．

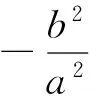
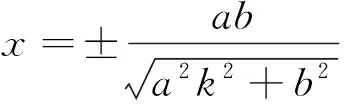
分析4:利用极坐标方程进行求解．

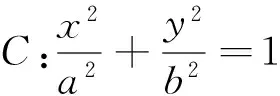
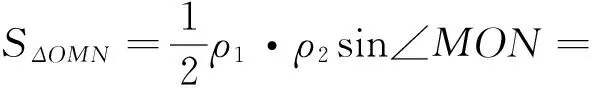
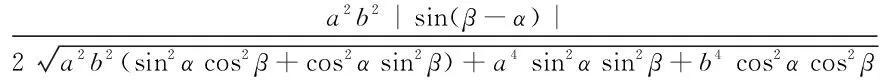
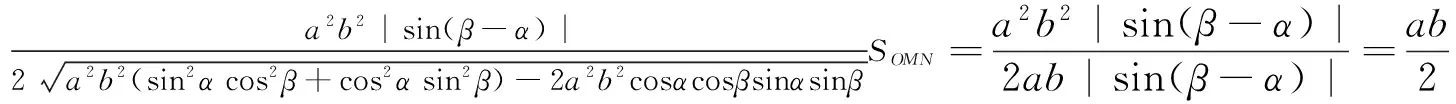
分析5:利用坐标伸缩变换知识把椭圆变为圆进行求解．

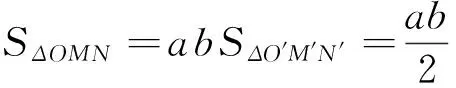
教育家波利亚说过：“没有一道题是可以解决得十全十美的，总剩下些工作要做，经过充分的探讨与研究，总会有点滴的发现，总能改进这个解答，而且在任何情况下，我们都能提高自己对这个解答的理解水平．” 通过以上多角度探究一道试题的一般情形，既能有效考查学生对所学知识的巩固程度，也能考查灵活应用所学知识分析问题和解决问题的能力．

[1]刘刚，赵毅．一道高考模拟试题的探究[J]．中学数学研究(江西)，2016，11．

[2]刘刚，赵毅．一道高考模拟圆锥曲线试题的探究与启示[J]．中学数学研究(江西)，2016，12．

*本文系北京市丰台区“十三五”重点课题《新课程背景下高中数学竞赛教学研究》(课题批准号：2016237-J)阶段成果之一．