一次说题活动的全纪录

浙江省金华市第六中学 (321000) 虞 懿

一次说题活动的全纪录

浙江省金华市第六中学 (321000) 虞 懿

随着新课程改革的深入，数学教研活动在内容和方式上也在不断地发生变化．由原来的“课堂教学”到“说课”，再到目前热行的“说题”活动，将教研内容范围逐步缩小，提高了课堂教学的针对性和有效性，体现了以小见大、去虚务实的教研理念，能更好地反映教师的基本功和提升青年教师专业水平．近期，笔者有幸参加了由市教研室组织的“说题”教研活动，受益匪浅，现将本次说题记录如下，供同行批评指正．

(2016年江苏高考第14题)在锐角三角形ABC中，若sinA=2sinBsinC，则tanAtanBtanC的最小值是 .

一、议审题扬帆起航

本题条件有两个：条件一是“锐角三角形ABC”；条件二是“sinA=2sinBsinC”，本题目标是“求tanAtanBtanC的最小值”.条件一的目的是什么？“锐角”大概是要保证tanAtanBtanC为正；“三角形ABC”能想到哪些？条件二怎么用？观察名称是三个角的正弦值，那么在三角形ABC中，任意一个角的正弦值等于另外两个角的和的正弦值，这是可以想到的.再来观察目标，如何求tanAtanBtanC的最小值？观察目标中角有三个，不是我们熟悉的一元函数，如何减元？而名称是三角形的正切值，三个角的正切值之间有什么联系？又如何实施从条件二中的正弦过渡到目标中的正切？只有启发学生把这些问题想清楚了，才能激发出学生解题的潜质.

二、探题源追本寻根

教材是知识的根本，教材是问题的源泉，教材也是高考试题的根源.面对经典的教材和浩瀚的资料，笔者认为，教材是已知世界，资料是未知世界.目前很多学生只喜欢资料，对教材却不是很熟悉，甚至很多高三学生连高一的教材都找不到了.笔者认为可由教师直接投影教材展现，这样既节省时间，又能引起学生对教材的重视.

题源1 苏教版《数学4》(必修)第116页的例4：

在斜三角形ABC中，求证：tanAtanBtanC=tanA+tanB+tanC.

不难看出，上述高考题的结论与这道例题的结论有相似之处，是这道例题的变式.

题源2 人教A版《数学4》(必修)第146页的复习参考题A组4(1):

证明：tanα+tanβ=tan(α+β)-tanαtanβtan(α+β)．

课本中的例习题是众多教材编写者智慧的结晶，每年的高考试题中都有一些以课本上的例习题为“根”而生成的．对这些题目的条件和结论加强或削弱、延伸或拓展，可真正达到对例习题的使用“源于课本，又高于课本”．

三、觅方法多维解析

学生解题中遇到的最大困难是条件与结论之间如何沟通，对于本题实质上就是正弦与正切之间如何转化．由条件想结论，将正弦化为正切，肯定是两边同除以余弦；由结论想条件，直接化正切为正弦即可．

解法1：由sinA=sin(B+C)=2sinBsinC得sinBcosC+cosBsinC=2sinBsinC，两边同时除以cosBcosC得tanB+tanC=2tanBtanC，设tanB+tanC=2tanBtanC=m，ΔABC为锐角三角形，则tanBtanC>1,m>2．

评注：解题难点在于由“tanAtanBtanC”的结构特点，明确“sinA=2sinBsinC”变形的目标和方向，进而推出“tanB+tanC=2tanBtanC”．倘若分析能力不足，那么可能不能明确变形方向，陷入“思维困境”．

解法2：同解法1可得tanB+tanC=2tanBtanC①,在斜三角形ΔABC中，有tanAtanBtanC=tanA+tanB+tanC．

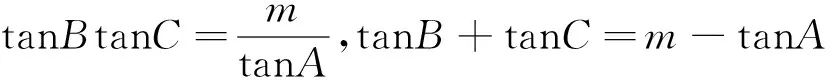
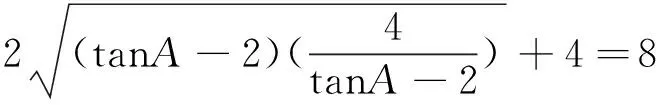
评注：本解法通过引入m进行换元，然后用代入法消元，将问题转化为求函数的最小值，最后借助均值不等式求出最小值．

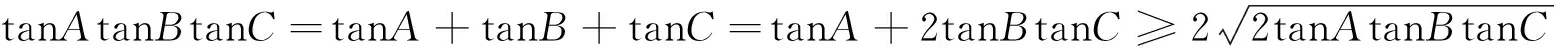
评注：本解法利用基本不等式求范围，但要熟悉结论“在斜三角形ΔABC中，有tanAtanBtanC=tanA+tanB+tanC.”

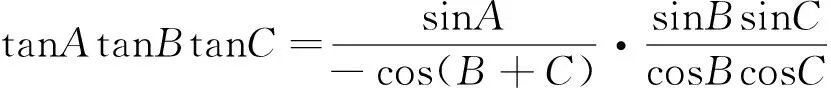
又(sinBsinC-cosBcosC)cosBcosC

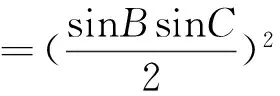
评注：本解法颇为巧妙，对学生提出了较高的思维要求，需要具备较强的洞察力并能熟练运用基本不等式．

四、说反思归纳感悟

数学思想方法和一些思维策略总是蕴含于学习活动之中的，学生获得数学思想方法的途径总的来说有两种，一是来自教师有意识的渗透和训练；二是来自学生自己在解题反思过程中的领悟．在解题后的“反思”过程中，通过反思与整合，把相关知识和方法提炼出来而形成的数学思想方法，学生才会有更深的体会，也更易于接受．也就是说，学生在反思过程中，反思自己是怎样发现和解决问题的，是如何找到突破口的，运用了哪些基本的思考方法、技能和技巧，其中又走过了哪些弯路，有哪些容易发生(或发生过)的错误，原因何在，该记住哪些经验教训等．在反思中认识和掌握数学思想方法，并用这种方法来指导自己进行数学学习与探究，从而对数学的理解实现由量变到质变的飞跃．

五、品思维赏析试题

从试题考查的知识点角度分析仅仅是复习了知识，如果从解题方法看，本题又是一个多元函数最值问题．那么牵及多元函数最值的一般解题思想是什么？如果不能直接用基本不等式或线性规划求解，可以考虑通过换元、消元的思想来达到减元，直至化为一元函数，以达到求最值的目的．解题的本质就是利用化归与转化的思想，这样的例子不胜枚举，可参见下面的试题拓展．教师引导学生多维解析的同时，可将解题过程中涉及的思想方法用彩色粉笔写在黑板的醒目位置，如化归与转化、消元法、换元法、基本不等式法等等．这样做的目的是授之以渔，而不是仅仅教给学生解题的过程．

六、谈变式引申拓展

解题是一种创造性活动，作为数学的学习，积累一定的解题经验对以后解题过程中快速提取信息应该是帮助很大的，而变式拓展则是解题经验自觉积累的有效途径．如在完成上面的高考问题探究后，若我们能从结论或条件的适当变化中编拟出一些问题，就可以巩固方法，辨析异同，提升能力．

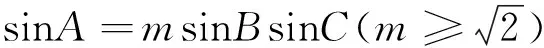
变式2 在锐角三角形ABC中，若sinA=2sinBcosC，则tanAtanBtanC的最小值是 .

变式3 已知三角形ABC中，若sinA+2sinBcosC=0，则tanA的最小值是 .

讲评试题时，教师不要就题论题、孤立地逐题讲题，要透过题中的表面现象，抓住问题的本质特征进行开放式、发散式讲解．

七、论启示服务教学

1．重视教材，用好教材

在课堂教学中经常看到这样一种现象：教师忽视对教材内容中知识的本质特征与内在联系的深入钻研，在课堂上只用很少的时间讲授教科书中的主要知识点，而将大量的时间用于做题，课后布置大量作业让学生反复做，本意是想弥补学生知识理解的不足，结果事倍功半，学生负担过重，苦不堪言．为了改变这种忽视教材、脱离教材的现状，减轻学生过重的学习负担，近年来高考数学试题加大了对教材例习题的改编力度，以期引导师生重视教材，用好教材，达到事半功倍的教学效果．教师只有深入挖掘教材，透彻理解教材，明确教材的编写意图，才能做到基于教材、超越教材，创造性地设计出符合学生学习规律、体现数学学科特点的教学过程，让学生在经历知识发生、发展的过程中学习数学知识，感悟数学思想，积累数学活动经验，逐渐由学会数学向会学数学转变．只有这样，学生在面临新的数学情境、新的数学问题时，才能从容淡定、应对自如．

2．把握核心，重视思想

数学核心内容、思想方法是高中数学学科体系的灵魂．在高中阶段，数学学科涉及的知识点汇成了数学结构系统的两条“河流”．一条是由具体的知识点构成的易于被发现的“明河流”，数学核心内容是“明河流”的主要交汇点，它是构成高中数学学科的“骨架”；另一条是由数学思想方法构成的具有潜在价值的“暗河流”，它是构成高中数学学科的“血脉”和灵魂．有了数学思想作灵魂，各种具体的数学知识点才不再孤立、零散．因为数学思想能将“游离”状态的知识点凝结成优化的知识结构，有了它，数学概念和命题才能活起来，做到相互紧扣，相互支持，组成一个有机整体．教师在教学中只有抓住数学核心内容、思想方法这一主线，才能高屋建瓴，取得更大的教学效益．学生只有真正把握了数学核心内容和重要的数学思想方法，才能跳出题海，走出就题论题的小路，走上以题论“法”、以题论“道”的大道．

总之，本次说题活动的尝试给教师专业化素养发展带来了一个全新的视角，笔者认为我们应该加强高考试题的研究，将有价值的数学问题通过说题的教学形式予以展示和交流，这样既发挥了优秀试题的典型性，也大大提高了教师对有价值试题的研究能力，使得教学水平得到进一步的提升．