解析几何问题中参数选择策略初探

江苏省江阴市华士高级中学 (214421) 王 炜 沈亚军

解析几何问题中参数选择策略初探

江苏省江阴市华士高级中学 (214421) 王 炜 沈亚军

1 问题缘由

解析几何问题信息量大、字母符号多、方法灵活、运算量大，能考查考生独立思考和运用所学知识分析问题、解决问题的能力，从而在高考中受到命题者的青睐.在高中解析几何的教学耗时多，尤其是在高三，教师和学生都投入了大量的时间和精力，并且在综合试卷讲评时都要重点讲解，课堂上学生听得懂，课后学生也非常重视，及时整理消化并找相关试题进行针对性训练，但考试的效果并不理想.

例如无锡市2017届高三(上)期末数学试卷第18题：

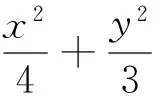
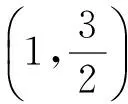
(2)设B(x1,y1),C(x2,y2)，且3y1+y2=0，求当ΔOBC面积最大时，直线l的方程.

该题第(2)问江阴市的得分情况如下表(满分8分，平均分0.16分)：

分数[0,1)[1,3)[3,5)[5,7)[7,8)8合计人数44172803912454757百分比92.85%5.89%0.82%0.25%0.08%0.11%100.00%

笔者所带班级的得分在区间[0,1)内的学生占到86.05%，平均分只有0.23分.通过数据统计及部分学生谈话，笔者了解到，致误原因多数是因为参数选择不当导致运算繁琐.

2 参数选择策略

策略一：设点(利用点B,C的坐标解题)

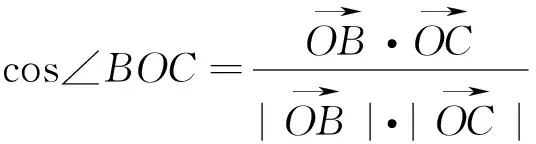
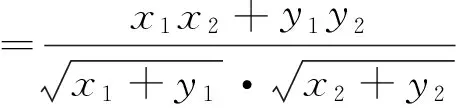
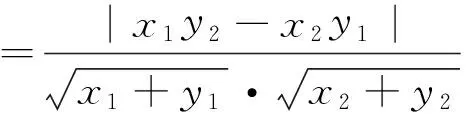
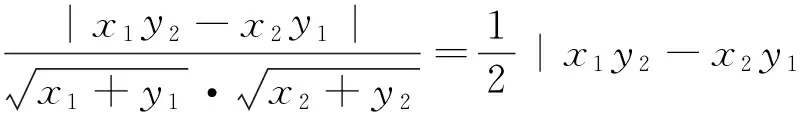
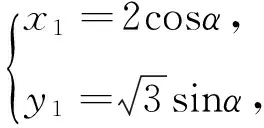
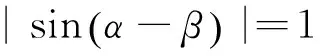
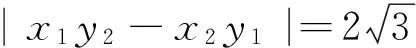
点评：字母多，运算量大，要求较高.

策略二：设线(设直线l的方程)

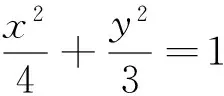
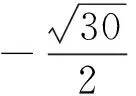
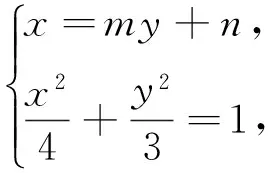
学习解析几何时，教师应该提供学生更多的独立思考和有信心实践的机会.是否还存在“懂而不会”的现象，及时检测就显得有必要，根据检测的结果对接下来的数学课堂作相应的调整和优化.该题参数的选择，设线优于设点，设直线l的方程为x=my+n优于设为y=kx+b，参数的选择可以从两方面考虑：①如何更高效的建立已知和目标之间的关系;②如何更好地消参.

从学生的检测情况如下：

[0,1)[1,3)[3,5)[5,7)[7,8)8合计69138524313.95%20.93%30.23%18.60%11.63%4.65%100.00%

平均得分3.60分，没有任何思路的学生有3人；选择解法1的学生有21人，但得分较低；选择解法2-1的有13人；选择解法2-2的学生有6人.说明通过这节课的学习，学生对于解析几何问题中参数选择策略的掌握已经有了不小提升，但离这一策略的完全掌握还有一段距离，也不可能通过一节课就完全掌握，这需要教师还要在后续的学习中持续跟进.

3 结语

波利亚说过：“掌握数学就是意味着善于解题，不仅要善于解一些标准题，而且善于解一些要求独立思考、思路合理、见解独到和有发明的题.”数学是教学生学会思考的一门学科，其核心能力是数学思维能力，解题过程不能局限于以往思路的“复制→粘贴”.课堂之所以充满生命的活力，就是因为教师面对的是一个个鲜活的生命体，那么教师在课堂上的主导作用和学生的主体作用均不可忽略.解析几何问题中参数选择策略，要求解题者独立尝试进行多种参数的选择，当第一思维受阻时，参数选择策略就起到关键性的作用.这正体现了解题思维的灵活性，既要能把思维发散出去，有效预判，又要能够从发散的思维中优化思维，从而有效解决解析几何问题. 学生对策略性知识的掌握不是一蹴而就的，教师必须遵循学生的认知规律，精心设计，留给学生足够的时间和空间进行真正的思维碰撞和实践机会，相信学生的数学思维能力能够得到长足的提升.

[1]鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.