一道离心率试题的命制与分析*

福建省泉州市第七中学 (362000) 吴宝树

一道离心率试题的命制与分析*

福建省泉州市第七中学 (362000) 吴宝树

在全国统一命题背景及新课程改革背景下，做好高三复习工作的一个重要环节就是命题工作.在认真研读全国卷考试大纲和考试说明的基础上，领会新课程改革对核心素养的要求，命制出有质量的试题，将会对考生的复习迎考起到很好的帮助.在本校的一次高三月考命题中，本人负责命制解析几何部分的试题，本文选取其中一道试题，分析试题的来源、命制过程及试题功能.

1 试题呈现

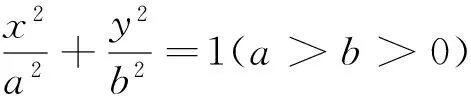
2 考查目标

本题考查了椭圆的离心率问题、等比数列通项公式、三角形边角关系、函数的单调性问题以及解不等式问题，综合运用了函数与方程的思想、转化与化归的思想、数形结合等数学思想，考查了学生的转化意识、数学语言互译能力及发现问题、分析问题、解决问题的能力.

3 命制过程

3.1 试题来源

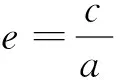
教材人教A版选修1-1第33页，给出椭圆焦点三角形图形: 椭圆的两个焦点F1,F2与椭圆上任意一点P组成的三角形.

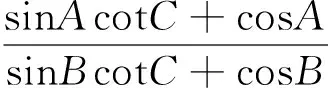
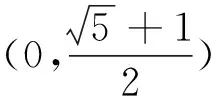
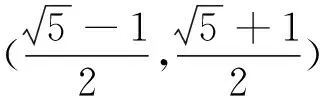
3.2 命制与改编

方案一 去繁就简

2008年这道联赛一试试题的核心问题是利用三角形两边之和大于第三边构造不等式，从而求得公比的范围.据此，可以得到如下题目：

题1 已知ΔABC的三边a,b,c成公比为q的等比数列，求q的取值范围.

方案二 改变背景

引入椭圆焦点三角形作为背景，将方案一中的三角形放在椭圆中，取椭圆的焦点三角形作为背景，在焦点三角形中，除了利用两边之和大于第三边构造不等式外，还要关注椭圆的焦半径a-c≤|PF|≤a+c这一隐含条件，题目的难度递进了一步.据此，可将题目改进如下：

题2 已知椭圆上存在一点P，F1,F2为左右焦点，若ΔPF1F2的三边|PF1|,|F1F2|,|PF2|成公比为q的等比数列，求q的取值范围.

方案三 改变设问

圆锥曲线离心率问题是考试的热点，也是难点问题，将最后设问与圆锥曲线离心率结合在一起，紧扣考试热点，同时也丰富了解法，拓宽了解题思路. 据此，可以得到如下题目：

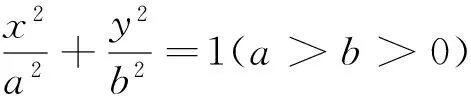
方案四 问题完善

在方案三的问题中，需要对|PF1|,|F1F2|,|PF2|的大小关系进行讨论，即分公比大于1或公比小于1两种情况，解题过程完全一致，显得比较繁琐.因此，可以适当降低试题的难度，最后成题的时候规定了|PF1|,|F1F2|,|PF2|的大小关系，既达到了考察目的，解题过程又不会显得过于繁琐. 据此，可以得到如下题目：

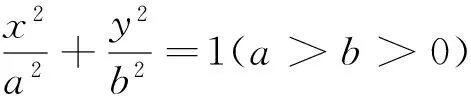
4 解题思路

本题题干简洁，易于学生快速把握题目的意思，从试题条件可以提取出如下信息：1、ΔPF1F2为焦点三角形；2、三角形的三边|PF1|,|F1F2|,|PF2|成公比大于1的等比数列.设问为求椭圆的离心率范围，需要根据条件构造不等式，并求出不等式的范围.解决此类问题经常用到定义法、函数单调性法、导数法、换元法、配方法、不等式法、数形结合法等解题方法，是高考中常见的题型.

解决本题有以下两种思路：

思路一：利用三角形两边之和大于第三边，构造不等式，运用函数与方程的思想转化为双勾函数处理求解.

思路二：由已知条件直接解出焦半径|PF1|，|PF2|，利用三角形两边之和大于三边，同时结合椭圆焦半径的范围构造不等式.

5 试题详解

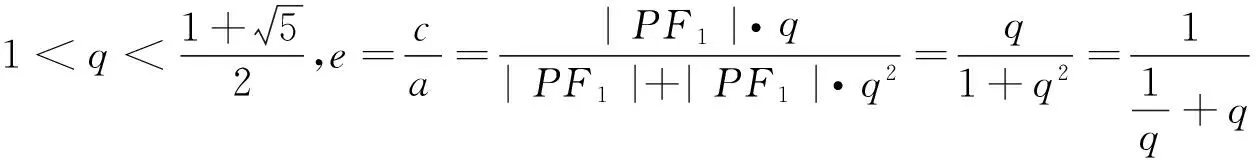
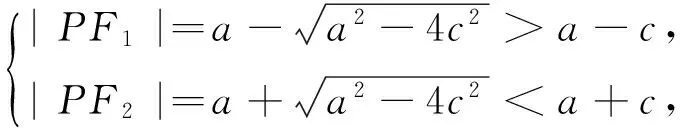
6 试题评价

本题属中档题，学生需要准确把握题目的意思，利用图形的直观特征，通过建模的思想，建立解决问题的模型，在模型的求解过程中，需要综合运用多种手段，才可得到正确答案.

这道试题充分体现了一道好的试题的功能和作用，充分考察了学生把握信息的能力和综合解决问题的能力.通过对一道联赛试题的变式和改造，充分地暴露了试题的生成过程和命制过程，充分发挥了直观想象，将建模的意识和数学学科的核心素养充分地融入到试题当中. 该试题一方面利用几何直观想象巧构数学函数问题，另一方面又把数学函数问题通过合理处理转化为几何直观图像想象问题，揭示了问题的本质.几何直观为高中数学学科核心素养之一，本题充分发掘图像的性质，利用三角形的边角关系以及椭圆的焦半径，构造不等式，求出椭圆离心率范围.从图形的直观特征出发，运用函数与方程的思想，求解出不等式的范围.直观解决问题教学这种重要手段，是探索和形成论证思路的思维根本.通过几何直观构造论证求解，揭示函数本质，体现思维自然规律.

[1]吴宝树.一道质检试题命题思路的剖析[J].中学数学研究(江西),2016(3):10-12.

[2]黄永生,杨丹.一道试题的解法思考与改编[J].福建中学数学.2015(10):14-15.

*本文为福建省教育科学“十三五”规划2016年度课题《基于全国Ⅰ卷函数与导数的考察研究》(课题编号：FJJKXB-314)的研究成果；也为福建省普教室2016年度课题《优化设计实践性作业，提高学生数学建模素养策略研究》(MJYKT2016-211)研究成果.