平面向量一道例题的拓展

江西省上饶中学 (334000) 吴选录

平面向量一道例题的拓展

江西省上饶中学 (334000) 吴选录

在北师大版高中教材必修4的《数乘向量》一节中有一道例题(例3)是关于三点共线的平面向量表达，笔者在对本例的教学中进行了拓展，引导学生探究直线的向量式方程，进而拓展到平面区域的向量表示.通过探究，培养了学生的发散思维、创新思维，渗透了化归转化的数学思想方法.

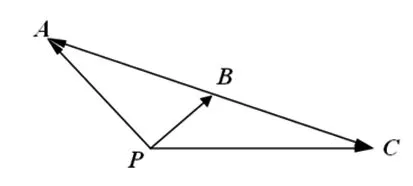
图1

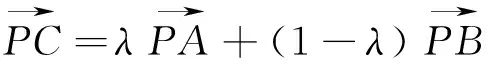
评析：①本题证明的关键是利用向量的共线关系，在共线的三点中选取两个向量，建立共线向量关系式，然后转化得到要证明的结论;②这道例题给出了判断三个点共线的一个方法，而实际上这道题还蕴含有更丰富的意义.

(1)当x+y=1时，点C构成的是什么图形？

(2)当x+y=2时，点C构成的是什么图形？

(3)当x+y=-1时，点C构成的是什么图形？

(4)当x+y=0时，点C构成的是什么图形？

(5)当x+y=c(c为常数)时，点C构成的是什么图形？

(6)当x+2y=1时，点C构成的是什么图形？

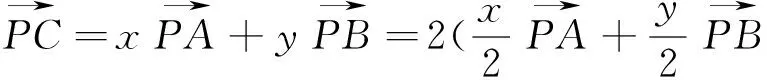
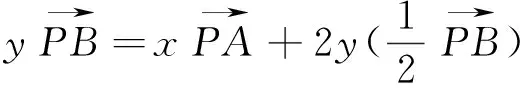
下面举几个应用以上有关结论的例子

例1 如图2，在三角形AOB中．

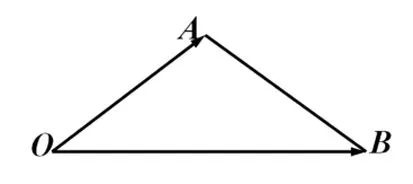
图2

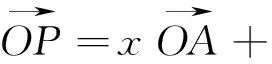
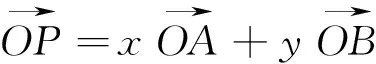
答：(1)x+y=1；(2)点P位于三角形ABC的内部．

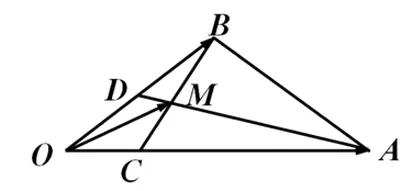
图3

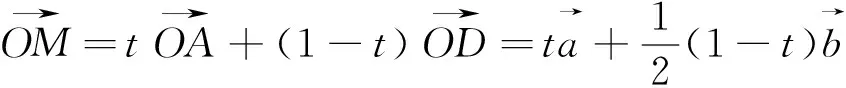
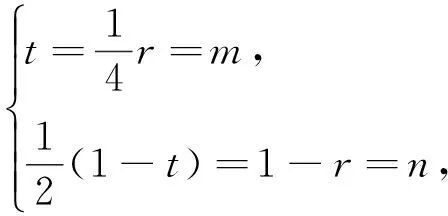
评析：点M的位置受到两组三点共线的制约，解题关键抓住两组三点共线，利用平面向量基本定理解决问题．

图4

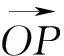
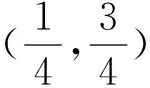
解析：图中区域满足，00，易得答案为D．

在平常的教学中，我们教师要深入钻研教材，发掘教材更深层次的作用，培养学生发现问题、分析问题、解决问题的能力.