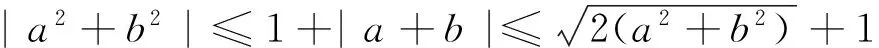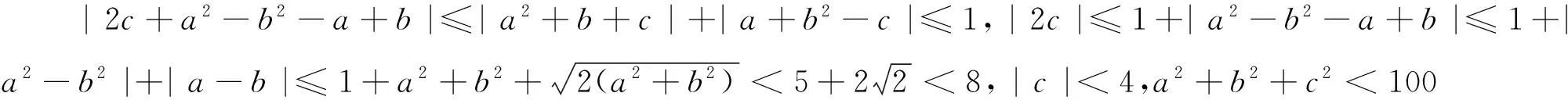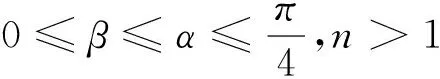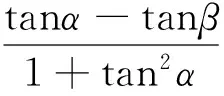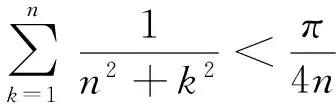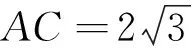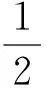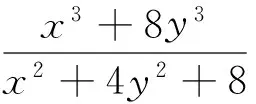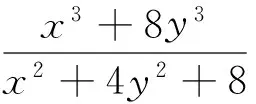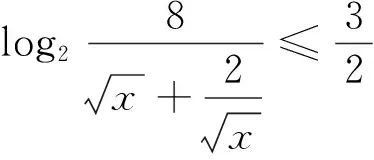例谈基于核心素养下的估算能力的培养
2017-07-05浙江省绍兴鲁迅中学312000陈少春
浙江省绍兴鲁迅中学 (312000) 陈少春
例谈基于核心素养下的估算能力的培养
浙江省绍兴鲁迅中学 (312000) 陈少春
最近笔者拜读了章建跃主任的《树立课程意识,落实核心素养》一文,在文中章博士提出数学育人的核心是对学生进行数学的思维和言语的教育,即经过数学的阅读、运算、推理和表达的训练,使学生正确理解数学知识,构成用数学知识合理解释直至创造性地处理问题的能力.应该去掉“非数学”的任务,让数学课的教学目标纯粹一些.对此笔者有些肤浅的感触,现将一些思考抛出,与同仁分享.
从高等数学的角度考虑,估算能力是一个科研工作者必须具备的一种能力,在思考解决某一问题的方法是否可行是需要科研工作者提前有一个大致的“预估”,不然会导致科研工作走弯路、岔路,浪费大量的物力、人力.同时估算能力不是与生俱来的,是需要后天培养的.因此浙江省高考数学《考试说明》在运算求解能力中明确提出:“能根据要求对数据进行估算,并能进行近似计算”.可见“估算”是运算能力的重要组成部分,是高考考查的能力之一.估算是以正确的算理和深刻理解研究问题的本质为基础,通过大体估值,合情猜想和特值探路等手段,进行粗略、近似地计算并获得正确答案的过程.这是一种更高层次的思维能力,在数学解题中渗透估算意识,有效地避免“小题大做,费时费力”的逻辑推理过程,达到简洁、快速、合理、准确解题的目的,恰到好处地契合了浙江高考命题倡导的“多考点想,少考点算”的基本理念,同时为学生进一步到高等学府做研究打下坚实的基础.那我们在平时教学中怎么培养学生的估算能力呢?
一、培养估算意识和兴趣
1.突出估算的重要性
估算在日常生活中虽然有广泛的应用,但由于教学的忽视和学生生活经验的缺乏,很少引起学生的注意.教师在教学中应多举实例,多加引导,让学生明白生活中处处要用到估算:点菜时事先估计餐费、外出时估计费用,估计完成一件工作所需的时间、装修预算、铺地面需要多少块砖,估计树的高度、湖面的宽度、楼层的高度等.学生在这些熟悉的、感兴趣的情境中自然而然感受到生活离不开估算.另一方面,学生很向往大学生活,在平时的教学中可以利用蕴含估算思想的大学知识来解高中数学问题,激发学生的估算兴趣.大学里微积分是一种重要的思维方法,它起源于极限思维、近似思维,在解决某些数列不等式放缩问题上事半功倍,过程简洁明了.
例1 (2014年陕西理21)设函数f(x)=ln(x+1),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的导函数.
(1)令g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N*,求gn(x)的表达式;
(2)若f(x)≥ag(x)恒成立,求实数a的取值范围;
(3)设n∈N*,比较g(1)+g(2)+…+g(n)与n-f(n)的大小,并加以证明.
解:(1)(2)略;
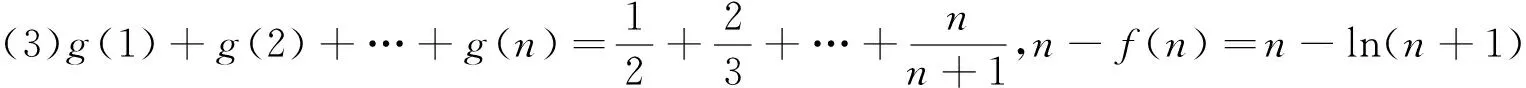

(1)求数列{an}的通项公式;
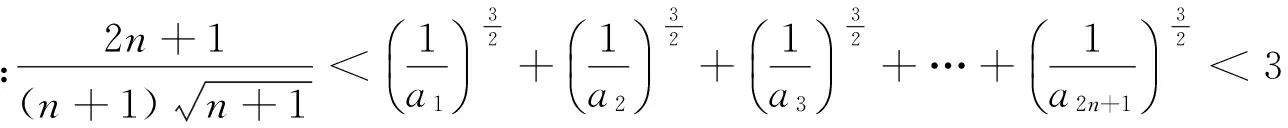
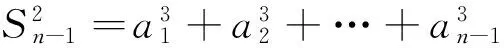

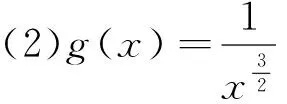
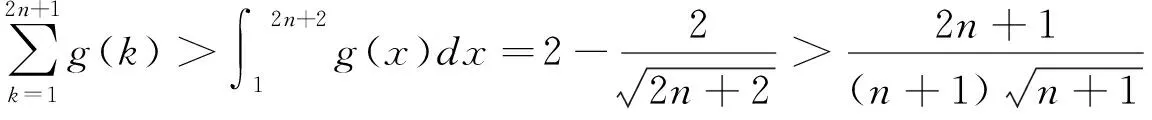
2.凸显估算的优越性
长期以来,学生受数学计算精确性的影响,看到题目,想到的是笔算,很少想到估算.教师可设计一些既可笔算,又可估算的题目,让学生用笔算与估算进行解答,通过两种方法的对比,形成强烈的反差,从而凸显估算的优越性,从内心上给学生以巨大的冲击.
|fk(a2)-fk(a1)|+|fk(a3)-fk(a2)|+…+
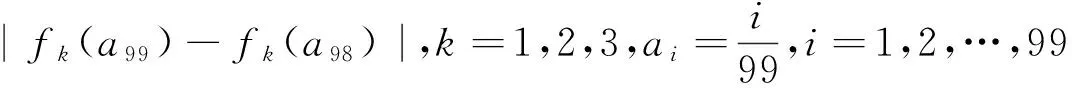
A.I1 C.I1 数学基础知识的重要性不言而喻,且现行高中教学改革和教学考试考查中对于基础知识的理解和把握越来越引起广泛的重视.根深之树不易折,泉深之水不会涸.因此在课堂上就需要把基础知识讲清讲透,通过举一反三,强化学生对基础知识的理解. 例4 (2015年浙江理7)存在函数f(x)满足,对任意x∈R都有( ). A.f(sin2x)=sinxB.f(sin2x)=x2+x C.f(x2+1)=|x+1| D.f(x2+2x)=|x+1| 这个问题考查的是函数周期性和对称性的性质:若函数g(x)是周期为T的周期函数,则f(g(x))也是周期为T的周期函数;若函数g(x)图像关于直线x=a对称,则f(g(x))图像也关于直线x=a对称.若学生掌握这个性质,上面那个选择题就可以估算“秒杀”. 例 (2013年浙江理8)已知e为自然对数的底数,设函数f(x)=(ex-1)(x-1)k(k=1,2),则( ). A.当k=1时,f(x)在x=1处取到极小值 B.当k=1时,f(x)在x=1处取到极大值 C.当k=2时,f(x)在x=1处取到极小值 D.当k=2时,f(x)在x=1处取到极大值 这个问题考查的是函数极值的概念,若学生对极值概念理解到位,那么选项C呼之欲出. 估算作为一种能力,集中表现在估算过程中需要运用各种有效策略,可以说“几乎不存在不用策略的估算”,有效的估算,都会或多或少用到一定的策略与方法.常用的估算策略有: 1.大体估值:比较大小,证明不等式问题 例5 (2016年浙江理8)已知实数a,b,c. A.若|a2+b+c|+|a+b2+c|≤1,则a2+b2+c2<100 B.若|a2+b+c|+|a2+b-c|≤1,则a2+b2+c2<100 C.若|a+b+c2|+|a+b-c2|≤1,则a2+b2+c2<100 D.若|a2+b+c|+|a+b2-c|≤1,则a2+b2+c2<100 2.特值探路:参数范围、离散问题 A.11B.9C.7D.5 例8 (2009年天津卷理10)0 A.-1 C.1 3.合情猜想:不等式、最值问题 例9 (2016年浙江理14)在ΔABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是 . 例11 设x,y,z>0,满足xyz+y2+z2=8,则log4x+log2y+log2z的最大值是. 解:由题xyz+y2+z2=8知y、z的数学逻辑地位是等价的,故可猜想当y=z时,log4x+log2y+log2z取到最大值,这时log4x+log2y+log2z= 合情猜想很多老师和同学认为这个方法不严谨,确实有时候我们的猜想是错误的,但是笔者觉得其实是体现一个学生的“数感”,东北师范大学史宁中说过:直觉思维在我们的数学研究中占有非常重要的地位,很多创新都是产生于直觉.为了能鼓励学生大胆、真实地估算,教师对估算结果的要求应该宽容一些,只要学生估算的答案在一定的合理范围之内,就应该得到肯定. 思想上重视,行动上落实,习惯上强化,一般性的目标一定可以实现.数学估算能力的培养也是一样,良好的数学估算意识养成,需要一个过程,而形成的关键是时间,因为根据科学家研究表明,一个好习惯、好意识的养成需要21天,90天的重复会形成稳定的习惯或意识,所以一个观念,如果被别人或自己验证21次以上,它一定会形成你的信念或意识.例如采用《好题本》(课堂和课外结合)收集好的估算题,做个有心人,那么提升数学估算能力和水平亦是指日可待.正所谓静待花开,芬芳自来.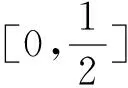
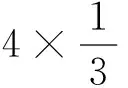
二、打实数学基础,掌握基本方法
三、有效积累和总结估算策略