“微元法”在电磁感应问题中的应用

■湖南省新田县第一中学 唐朝忠

“微元法”在电磁感应问题中的应用

■湖南省新田县第一中学 唐朝忠

微元法又叫微小变量法,是分析、解决物理问题的常用方法之一。在由导体棒切割磁感线引起的电磁感应现象中,若回路闭合,则导体棒中将产生感应电流,使得导体棒受到安培力的作用,导体棒在安培力的作用下,其速度将变化,速度的变化将导致安培力发生变化,进而导致导体棒的加速度也发生变化。运用微元法求解此类电磁感应问题将会获得事半功倍的效果。

一、导体棒只受安培力作用

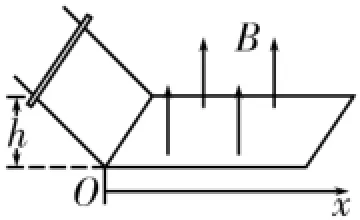
如图1所示,宽度为L的光滑金属导轨一端封闭,电阻不计,足够长。导轨的水平部分处在方向竖直向上、磁感应强度大小为B的匀强磁场中。质量为m、电阻为r的导体棒从高度为h的导轨的倾斜部分上由静止开始滑下,导体棒由于在磁场中受安培力的作用,在导轨的水平部分上滑行距离s后停下。

(1)求导体棒刚滑到导轨的水平部分上时的速度v0。

(2)写出导体棒在导轨的水平部分上滑行的速度v与在导轨的水平部分上滑行的距离x的函数关系。

解析：(1)导体棒在从静止开始刚好滑到导轨的水平部分上的过程中,由机械能守恒定律得mgh=mv20,解得v0=

(2)当导体棒在磁场中的速度为v时,受到的安培力大小F=BIL=,安培力安的方向与速度v的方向相反。因为安培力是变力,所以需要使用微元法将变力问题转化为恒力问题。在极短时间Δt内,导体棒受到的安培力可以看成恒力,设导体棒的加速度为a,则由牛顿第二定律得F安=ma,解得在极短时间Δt内,导体棒速度的变化量为-vΔt,又有vΔt= Δx,因此在时间t内导体棒速度的变化量·vΔt=-,则v= v+Δv=。

点评:微元法是将研究的对象或过程进行无限细分,以达到化变为恒、化曲为直的目的。本题第(2)问利用微元法将变力问题转化为恒力问题,分析微小恒力所遵循的物理规律,然后将与每个微小恒力相关的物理量累加求和,从而顺利求得速度v与位移x的函数关系。

二、导体棒既受安培力又受重力作用

图2

如图2所示,在竖直平面内有一边长为L、质量为m、电阻为R的正方形金属线框,竖直向下的匀强重力场和水平方向的磁场组成了一个复合场,磁场方向与线框平面垂直,磁感应强度大小随竖直向下的z轴按B=B0+kz的规律均匀增大。将线框在复合场中以初速度v0水平抛出,重力加速度为g,求:

(1)线框的竖直分速度为v1时,线框中瞬时电流的大小。

(2)如果线框从开始抛出到瞬时速度大小为v2所经历的时间为t,那么线框在时间t内的竖直分位移大小为多少?

解析：(1)因为线框左右两边切割磁感线产生的感应电动势抵消,线框上下两边所在处的磁感应强度大小不同,所以线框中感应电流的大小

(2)线框受重力和安培力作用,其中重力mg为恒力,安培力为变力,因此可以把线框的运动分解为在重力作用下的匀加速运动和在安培力作用下的变加速运动。线框在重力作用下,在时间t内增加的速度(Δv)1=gt。设在极短时间Δt内,变力可以看成恒力,变加速运动可以看成匀加速运动,则线框在安培力作用下的加速度,在极短时间Δt内速度的增加量Δt,又有vzΔt=Δz,因此在时间t内线框因安培力的作用而增加的速度。由运动的合成知在时间t内总的增加的速度为从宏观上看时间t内速度的增加量为,即解得

点评:本题中线框虽然在复合场中受到重力和安培力两个力的作用,但是因为重力是恒力,安培力是变力,所以需要先将线框的运动分解成重力作用下的自由落体运动和安培力作用下的变加速运动,再利用微元法将变力问题转化成恒力问题,最后运用运动的合成求解线框的位移。

三、导体棒受到的重力和安培力不在一条直线上

图3

如图3所示,两平行光滑金属导轨安装在一光滑绝缘斜面上,导轨间距为L、足够长且电阻忽略不计,斜面倾角为α。条形匀强磁场的宽度为d,磁感应强度大小为B,磁场方向与斜面垂直。长度为2d的绝缘杆将导体棒和正方形单匝线框连接在一起形成一个整体装置,其总质量为m,置于导轨上。导体棒中通以大小恒为I的电流(由外接恒流源产生,图中未画出)。线框的边长为d(d〈L),电阻为R,下边与磁场区域上边界重合。将装置由静止释放,导体棒恰好运动到磁场下边界处返回。导体棒在整个运动过程中始终与导轨垂直,重力加速度为g。求线框第一次穿越磁场所需的时间t0。

解析：设线框刚离开磁场下边界时的速度为v1,则线框将继续向下运动2d,由动能定理得,解得线框在第一次穿越磁场的过程中,装置在磁场中受到的合力F=mgsinα-F',感应电动势ε=Bdv,感应电流安培力F'=BI'd,由牛顿第二定律可知,在t到t+Δt时间内,有Δv=,则即解得t=0

点评:本题中装置受到的重力和安培力不在一条直线上,如果按照例2的方法将导体棒的运动分解成在重力作用下的运动和在安培力作用下的变加速运动,则会使解题过程烦琐,且容易出错。

(责任编辑 张 巧)