LLC谐振变换器模糊自适应控制研究

吴建明，汪 伟，蔡 慧

(中国计量大学 机电工程学院，浙江 杭州 310018)

LLC谐振变换器模糊自适应控制研究

吴建明，汪 伟，蔡 慧

(中国计量大学 机电工程学院，浙江 杭州 310018)

LLC谐振变换器由于其高效率、高功率密度和软开关特性，在众多领域得到了广泛的应用.然而目前普遍采用的是电压控制模式，在该种控制模式下动态响应较慢，不能很好适应LLC谐振变换器的宽负载变化要求.针对这一问题，我们设计出一种模糊自适应控制方式，使LLC谐振变换器在不同的负载和输入电压的情况下都能快速稳定地响应.并且详细分析了其工作原理并给出了关键设计，最后还通过仿真验证了这种控制方法具有更快的动态响应速度.

LLC谐振；自适应控制；变换器；模糊PID

LLC 谐振变换器具有良好的软开关优势，在全负载范围下都可以实现零电压开关，并且高频化和磁集成技术可以有效地减小变换器体积，易实现变换器高效率与高功率密度的要求，这使得其得以广泛应用于电池充电、通信电源等众多领域[1].目前LLC谐振电路反馈回路普遍采用电压型控制模式，在该种控制模式下变换器具有动态响应速度较慢的缺点，难以适应宽负载变化的要求.

LLC谐振电路因其工作的复杂性，很难建立准确的小信号模型[2]，又由于在不同的工作条件下谐振网络增益变化曲线不同，因此用传统的控制方法实现快速动态响应均比较复杂.目前改进的方法一般有电流模式[3]和近似时间最优控制方式[4]，前者需要另外增加电流采样电路，增加电路设计难度，且受误差放大器及补偿电路的影响而仍然具有低瞬态响应速度的特点；后者能实现快速反应，但其控制器设计的复杂程度非常高，难以广泛应用.模糊自适应控制可以不用依赖准确的系统模型，根据反馈信号，通过模糊规则对PID参数实时调节[5]，使变换器在不同的工作条件下均有较快的动态响应.在文献[3]中提出了平均电流控制以及文献[6]中提出了谐振电容电压型控制，他们需要增加采样和反馈回路，从而增加了控制电路设计的复杂性.文献[7]中提出的自动转换最小误差控制通过PID控制器和瞬态抑制器之间的切换实现快速调节，在参数匹配的情况下能得到较好的性能，但在系统参数有变化时不能保证理想的控制性能.

模糊控制在智能控制领域理论研究相对比较成熟，且相对比较容易实现，因而得到了广泛的应用.模糊控制算法可依据经验进行控制器的设计，按照模糊规则实时调节参数.所以，本文将通过对LLC谐振变换器的原理及工作特性进行分析，在传统的PID控制基础上结合自适应模糊控制设计一个控制器.该控制方法既利用了经典控制技术的简单、灵活性，还充分发挥模糊控制对非线性系统进行快速整定的优点.控制器以输出电压误差e和归一化频率fn为输入对PID参数进行实时调节，不需要另外增加采样反馈回路，对不同的LLC谐振电路也有很好的适应性.最后通过与传统的电压型控制进行对比以验证其效果.

1 LLC串联谐振变换器

1.1 变换器拓扑结构及工作原理

全桥LLC谐振主电路拓扑结构如图1，其中，Q1～Q4为4个MOSFET管及其体二极管，C1～C4为寄生电容，谐振电容Cr、谐振电感Lr和励磁电感Lm组成谐振网络，变压器比为n，与变压器副边相连的二极管D1～D4组成全桥整流电路，Cf即输出电容，RL为负载.

图1 全桥LLC谐振变换器Figure 1 Full bridge LLC resonant converter

LLC谐振变换器主电路可分为三个部分，逆变部分、谐振网络和副边整流部分.逆变部分功率管以固定的50%占空比互补导通(实际中有死区).谐振网络包含两个谐振电感和一个谐振电容，谐振电感Lm、Lr和谐振电容Cr主要作为分压器.

(1)

由式(1)可知其阻抗随工作频率的改变而改变，所以可随负载的变化而改变频率以调节输出电压Vout.整流网络则是对谐振网络产生的正弦波形进行整流，然后传输到输出级.

1.2 频率特性分析

LLC谐振变换器的谐振网络中有两个串联谐振电感Lm、Lr和一个串联谐振电容Cr，在谐振网络中也就形成了两个谐振频率[8].

当副边二极管导通时，变压器副边电压嵌位励磁电感Lm，Lm两端电压恒定不参与谐振，只有谐振电容Cr、谐振电感Lr参与谐振，定义谐振频率为

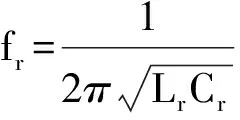
(2)

而当副边整流二极管处于截止状态时，就相当于变压器与副边断开，此时没有能量传递到副边，Lm也不再被副边嵌位，谐振电容Cr、谐振电感Lr和励磁电感Lm都参与谐振.定义此时谐振频率为

(3)

LLC谐振变换器是通过改变开关频率fs来调节输出的，根据开关管的开关频率fs与谐振频率的fr、fm的关系可将变换器的工作状态分为fs>fr、fm

谐振网络常用基波分析法(FHA)进行稳态分析，可以得到谐振网络的电压增益为

(4)

由式(4)可知，谐振网络的增益主要受参数K值和Q值影响.当电感比K值变大时，全桥LLC谐振变换器的直流增益曲线就会变得缓慢，增益的变化范围也会随之减小，可能导致输出电压无法调节到所需的值.当电感比K值减小时，则会使得变压器损耗增加，因此K值不宜过大也不宜过小[9].

对于控制器的设计需要重点分析不同Q值即不同的负载情况下谐振网络电压增益的变化，图2为通过MATLAB软件绘制的不同负载情况下的增益曲线，其中K值为7.根据开关管是否实现ZVS以及后级整流是否实现ZCS将LLC谐振变换器工作状态分为3个区域:区域1谐振电路工作在容性状态，电流超前电压的变化，不能实现初级开关管的ZVS；区域2谐振电路工作在感性状态，能实现初级开关管的ZVS，次级整流管电流也会自然过零，实现ZCS，是谐振电路工作的最佳区域；区域3谐振电路工作在感性状态，能够实现开关管的ZVS，而次级整流管电流不能实现ZCS.

图2 谐振网络电压增益曲线图Figure 2 Resonant network voltage gain curve

从图2中可以发现，不同的负载对应着不同的增益曲线，每条曲线都是随频率的增大先快速增大然后慢慢减小.并且非谐振点的增益会随负载的增大而减小，所能到达的最大直流增益也越小，但所有的曲线都经过同一点，即归一化频率等于1时的点，此时工作频率等于谐振频率，电压增益不随负载的变化而改变，谐振网络的增益为1.从图2中可以看出在不同的频率段增益随负载变化而改变的大小也不一样，在归一化频率越接近1时其变化越小，在0.4～0.5附近变化最大.

2 模糊自适应控制工作原理

传统的控制是采用输出电压作为反馈信号，经过PID调节对频率进行调节，这种模式结构简单，容易实现，且能有不错的稳压效果，因此应用广泛.然而由上文对增益特性分析可知LLC谐振变换器的电压增益是非线性变化的，且在不同的负载条件下增益响应曲线不同，所以普通PID电压控制方式难以在变换器不同的工作条件下都实现快速稳定的调节.

模糊控制可以不要求被控对象的精确模型且适应性强，非常适应模型不确定的非线性系统.但是单纯的采用模糊控制，不仅难以制定确定的模糊规则，且难以完全消除稳态误差.因此，本文结合两种控制的优点，采用的是模糊PID控制，它可在线调整PID参数，不仅保持了PID 控制系统可靠性、实时性等特点，还具有更好的适应性，非常适用于LLC谐振变换器当中.

控制器由采样模块、模糊逻辑控制模块、PI控制模块和驱动电路组成.在传统的PI电压控制模式下加入模糊逻辑控制器，整体结构如图3.

图3 自适应模糊控制整体结构框图Figure 3 Block diagram of adaptive fuzzy control

一般模糊逻辑控制器以输出电压误差e以及误差变化率εe作为输入语言变量，Kp、Ki为模糊逻辑控制确定输出语言变量.由前文对变换器的分析可知，电压增益是通过频率进行调节的，且由图2的电压增益曲线可知，增益随频率的变化而变化的快慢也与频率大小有关，当开关频率小于谐振频率时，即工作在图2中的区域2，频率变化斜率随频率的增加而明显变缓.因此，模糊逻辑控制器以输出电压误差e和当前的开关频率归一化的值fn为输入语言变量，Kp、Ki为模糊逻辑控制确定输出语言变量.通过模糊推理对PI控制参数实时调节.

推理规则设计的原理主要是通过当前工作频率归一化的值判断电压增益的变化速率，结合误差的大小及方向估计需要调整的频率范围，以此确定ΔKp和ΔKi值.

再根据变换器频率特性分析可知，在不同的频率段增益随负载的变化而变化的程度差别较大，并且在不同的频率下电压增益变化速率差别也较大.由图2中所示可按归一化频率fn大小将工作状态划分为四段，分别为:0.4～0.6段增益曲线最陡，0.6～0.8段曲线偏陡，0.8～1和大于1段的情况曲线都较平缓.模糊逻辑控制规则即是在频率较低时曲线较陡，增益随频率变化明显，应减弱控制效果；在频率较高时曲线较缓，增益随频率变化不明显，应增强控制效果.当负载增加，电压增益曲线整体变缓，则应增强控制效果；当负载减小，电压增益曲线整体变陡，则应减弱控制效果.例如，在变换器工作频率归一化值在0.6～0.8段，且当误差为正时，需增大频率减小电压，但增益变化速率会随频率增加越来越慢，所以需增大Kp加快反应速度；但当误差为负时，则需减小Kp以提高系统稳定性.

3 模糊逻辑控制器设计

模糊逻辑控制器以输出电压误差e和开关频率归一化的值fn为输入语言变量，ΔKp和ΔKi为模糊逻辑控制确定输出语言变量，通过改变ΔKp和ΔKi的值而调整参数Kp和Ki值.其中模糊控制的输入语言变量e和输出变量ΔKp和ΔKi都为7个模糊子集，分别表为正大(PB)、正中(PM)、正小(PS)、零(ZO)、负小(NS)、负中(NM)、负大(NB).其中正大(PB)和负大(NB)的隶属度函数采用高斯函数，而正中(PM)、正小(PS)、零(ZO)、负小(NS)和负中(NM)均采用三角函数作为隶属度函数，如图4所示为输出电压误差的隶属度函数图.输入变量fn采用5个模糊子集，分别表为正(PM)、零(ZO)、负小(NS)、负大(NB).其中正(PM)和负大(NB)的隶属度函数采用高斯函数,零(ZO)、负小(NS)采用三角函数作为隶属度函数.

图4 输出误差e隶属度函数图Figure 4 Output error e membership function graph

模糊逻辑控制器需要根据控制规则进行逻辑判断，控制规则是根据对控制对象即LLC谐振变换器的分析和文献[10-12]等中总结经验制定，再通过实验验证进行优化和修改.主要按以下方法进行规则制定：当误差较大时，需要快速的动态响应，应当取较大的Kp值；在误差变化在中等值时，需要控制超调和加快响应速度，取较小的Kp和适中的Ki；当误差较小时，为了提高稳态误差应当取较大的Ki和适中的Kp值.例如，在启动停止时，输出电压误差e较大，模糊化为NB或PB时，则应使ΔKp为PB、PM或PS，对Kp进行按比例增大.当输出到达稳定状态时，输出电压误差e接近0，则ΔKp应为NB、NM或NS对Kp减小,ΔKi为PB、PM或PS对Ki增大.

当频率归一化在1附近时，增益随频率变化较小，在存在误差的情况下应加大Kp值以加快系统的响应速度；当频率归一化在较小的情况下，增益随频率变化较大，且在不同负载情况下增益不同.所以，在存在正误差的情况下，应减小Kp和提高Ki以提高系统的稳定性和减小波动；在误差为负值情况下应提高Kp和减小Ki加快响应速度.例如:当存在误差，fn在PB时的ΔKp要比在NB是ΔKp大.

模糊控制规则表如表1.

表1 模糊规则表

PI控制器参数按下式确定

(5)

模糊控制器实时调节Kp、Ki值是在原来的值上乘以相应系数ΔKp和ΔKi，通过对这个系数的实时调节以实现改变Kp、Ki的大小.

4 仿真结果

根据所设计的模糊PID自适应控制器，在MATLAB/Simulink中对全桥LLC的控制性能进行仿真.全桥LLC谐振变换器主要参数如下:直流输入电压为170～195V，输出额定电压为24V，输出电流为1～6A，谐振频率为58kHz，开关频率为30～120kHz，Lm=1240μH，Lr=160μH，Cr=47nf，控制器的PI参数分别为Kp=7、Ki=4000.

将本文设计的模糊控制结果与传统的电压型控制结构进行对比，如图5所示输入电压为195V，负载电流从1A突变到6A和从6A突变到1A时输出电压动态响应对比图.

由对比图5(1)可见，在传统电压型控制模式下，当负载突然增大时，电流由1A突变到6A,输出电压降落为486mV，调整时间约9ms；当负载突然减小时，电流从6A突变到1A，输出电压超调为317mV，调整时间约8ms.由图5(2)可见，在模糊自适应控制下，负载增大时，输出电压降落288mV，调整时间为3ms；负载减小时，输出电压超调231mV，调整时间为4ms.由此可见，模糊自适应控制模式在负载突变的情况下不仅有更快的动态响应速度，而且减小了输出电压的波动幅度.可见，在负载突变时模糊自适应控制有更好的动态响应.

图6为负载1A，输入电压从195V突变到170V，再从170V突变到195V输出电压的动态响应对比图.

图5 负载动态响应对比图Figure 5 Comparison of dynamic load response

图6 输入突变动态响应对比图Figure 6 Comparison of the dynamic response of input mutation

由对比图6(1)可见，在传统电压型控制模式下，当负载不变，输入电压由195 V突变到170 V时，输出电压降落为521 mV，恢复调整时间约11 ms；当输入电压由170 V突变到195 V时，输出电压超调为430 mV，调整时间约8 ms.由图6(2)可见，在模糊自适应控制下，输入电压由195 V减小到170 V时，输出电压降落304 V，调整时间为约为4 ms；输入电压再恢复到195 V时，输出电压超调319 mV，调整时间为7 ms.由此可见，模糊自适应控制在输入电压突变时比传统电压控制模式动态响应速度更快，输出电压的波动幅度更小.所以在输入电压发生波动的情况下模糊自适应控制有更好的动态响应.

5 结 语

本文通过深入分析LLC谐振电路增益特性，并结合现代智能控制设计出一个具有自适应性能的控制器.同时详细的分析了其控制原理，并给出了其具体的设计方法.该控制器能在负载变化和输入电压波动等不同的工作条件下均能实现快速的动态响应，保证电压稳定输出.同时此控制器不需要额外增加采样电路，且设计简单，容易实现，对不同的LLC谐振电路有很好的通用性.

[1] ZHONG S,XU J P, ZHAO S, et al. Bi-frequency control for LLC resonant converter with fast transient response [J]. Institution of Engineering and Technology,2016,52(20):1710-1712.

[2] 梁昊，张军明.一种简化的LLC谐振变换器小信号分析方法[J].电力电子技术,2011,45(10):71-72,95. LIANG H， ZHANG J M.A simplified small-signal analysis method for LLC series resonant converter[J]. Power Electronics,2011.45(10):71-72,95.

[3] JANG J,KUMAR P S,KIM D, et al. Average current-mode control for LLC series resonant DC-to-DC converters[C]//International Power Electronics and Motion Control Conference (IPEMC), Harbin:IEEE,2012:923-930.

[4] WANG F, LEE F C, MATTAVELLI P. Simplified optimal trajectory control (SOTC) for LLC resonant converters[J].IEEE Transactions on Power Electronics,2013，28(5):2415-2426.

[5] 崔雅静，杜艳丽，王晓雷.自适应模糊PID控制器的设计[J].控制工程,2008,15(增刊2):128-129,157. CUI Y J, DU Y L, WANF X L. Design of self-adaptive fuzzy PID controller[J].Control EnginSeering of China,2008,15(suppl 2):128-129,157.

[6] 姜龙飞，高建龙.谐振电容电压控制LLC谐振变换器分析与设计[J].电力电子技术，2016,50(9):48-50. JIANG L F, GAO J L. Analysis and design of resonant capacitor voltage controlled LLC resonant converter[J].Power Electronics,2016,50(9):48-50.

[7] MARYAM S A, BEHZADM, ALEKSANDAR P. Auto-tuned minimum-deviation digital controller for LLC resonant converters [C]//Energy Conversion Congress and Exposition (ECCE).Montreal:IEEE,2015:1723-1728.

[8] IVENSKY G，BRONSHTEIN S，ABRAMOVITZ A.Approximate analysis of resonant LLC DC-DC converter[J].IEEE Transactions on Power Electronics,2011,26(11):3274-3284.

[9] YU R，HO G K Y， PONG B M H, et al.Computer-aided design and optimization of high efficiency LLC series resonant converter[J].IEEE Transactions on Power Electronics,2012,27(7):3243-3256.

[10] 窦亮亮,徐伟中,李雄，等.温室环境模糊控制器的设计[J].中国计量学院学报,2007,45(1):34-37，53. DOU LL, XU W Z, LI X, et al. Application of fuzzy control in greenhouse environment control systems[J].Journal of China University of Metrology,2007，45(1):34-37，53.

[11] 陈家伟,陈杰,陈冉,等.变速风力发电机组自适应模糊控制技术[J].中国电机工程学报,2011,31(21):93-101. CHEN J W, CHEN J, CHEN R，et al. Adaptive fuzzy logic control technique for variable-speed wind turbines[J].Proceedings of the CSEE,2011,31(21):93-101.

[12] BETIN F， PINCHON D， CAPOLINO G A. Fuzzy logic applied to speed control of a stepping motor drive[J].IEEE Transactions on Industrial Electronics,2000,47(3):610-622.

Research on adaptive control of LLC resonant converters

WU Jianming, WANG Wei, CAI Hui

(College of Mechanical and Electrical Engineering, China Jiliang University, Hangzhou 310018, China)

The LLC resonant converter has been widely used because of its high efficiency, high power density and soft switching characteristics. However, the commonly used voltage control mode cannot adapt to the requirements of the LLC resonant converter because of its slow response. To solve this problem, we designed a kind of fuzzy adaptive control method to impove the response and stability of the resonant converter under different loads and input voltages. The principle of the system was analyzed and the key design was given. The simulation results show that the control method has a faster dynamic response.

LLC resonance; adaptive control; converter; fuzzy PID

2096-2835(2017)02-0196-07

10.3969/j.issn.2096-2835.2017.02.010

2017-02-26 《中国计量大学学报》网址：zgjl.cbpt.cnki.net

国家自然科学基金青年基金资助项目(No.51407173).

吴建明(1992-)，男，江西省九江人，硕士研究生，主要研究方向为DC/DC变换器.E-mail:273259279@qq.com 通信联系人：蔡慧，男，副教授. E-mail: caihui@cjlu.edu.cn

TP273.4

A