一种FIR频率平面滤波器及其在光场滤波中的应用

方力，叶龙，钟微，张勤

(中国传媒大学 媒介音视频教育部重点实验室，北京 100024)

一种FIR频率平面滤波器及其在光场滤波中的应用

方力，叶龙，钟微，张勤

(中国传媒大学 媒介音视频教育部重点实验室，北京 100024)

本文提出了一种FIR频率平面滤波器，它具有近似4D平面的通带形状。该滤波器的设计基于窗函数法，设计简单，且具有线性相位特性，因此非常适合用于光场处理。理论分析和实验表明，由无遮挡朗伯表面构成的光场可以使用该滤波器实现深度滤波。

4D滤波器；光场；场景分析；窗函数法；线性相位

1 引言

基于图像渲染(Image-based Rendering)模拟场景中弥漫的光的行为，而不是采集场景的几何形状和纹理，能够从预先采集的视图中生成一个新的视图，而不依赖于场景的几何信息。光场(Light Field)渲染及其变种[1，2]模拟与场景相关联的7D全光函数(Plenoptic Function)[3]的一个4D子集，是一种重要的基于图像渲染技术。相比于基于模型渲染(Model-based Rendering)方法，它的复杂度不依赖于场景的复杂度，易于实现实时渲染，因此近些年来吸引了大量的研究兴趣。

7D全光函数描述了光在时间(一维)、空间(三维)、方向(二维)和频率(一维)一共七个维度的行为。在透明介质的无遮挡静态场景中，它可以被简化为一个4D函数[1]。4D光场通常使用两平面参数化(Two-plane Parameterization，2PP)来表示光线，如图1所示。每条光线由它与两个参考平面的交点来描述：其中一个平面被称作相机平面，用(s，t)表示，另一个是焦平面，用(u，v)表示。一个完整的光场可以包含多组这样的平面。注意颜色通常不被算在光场的维度里，因为它们通常被分成红、绿、蓝三个通道单独处理。

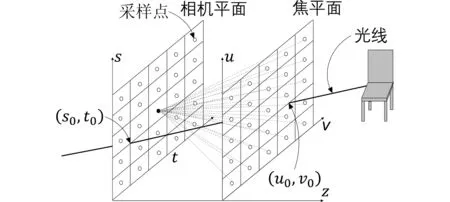
图1 四维光场的两平面参数化

关于光场的滤波，许多人取得了许多研究成果。1996年Gortler和Szeliski等人提出了具有深度补偿的四线性插值滤波器[2]，证明了深度信息对于提高重光场建质量是非常重要的。2000年Chai和Shum等人分析了光场的频谱，给出了最优恒定深度重建滤波器[3]。2004年Zhang使用特征滤波器的方法设计了一个蝶型滤波器用来重建光场[4]。2003年Dansereau和Bruton 提出了一个频率平面IIR滤波器[5]，能够实现光场的深度滤波器。2007年他们又提出了一个双扇形IIR滤波器[6]，能够提取场景中一定深度范围的光场。2013年Dansereau提出了一个频域超扇形滤波器[7，8]，用于光场去噪和生成全景聚焦图像。2015年Edussooriya等人提出了一组IIR深度-速度滤波器[9]，用于动态光场处理。然而，上述这些滤波器中大部分都是IIR滤波器，需要级联额外的网络才能实现线性相位(Linear-phase，LP)特性或者零相位滤波，设计灵活性差。

针对这个问题，本文提出了一种具有线性相位特性的FIR频率平面滤波器，可以实现光场的深度滤波。论文其余部分结构安排如下：第二节展示了一个朗伯场景(Lambertian Scene)可以使用4D频率平面滤波器实现深度滤波；第三节给出了这样的滤波器的设计方法；第四节给出了实验结果；第五节讨论了结论。

2 朗伯场景的频谱特性

2.1 全向点光源的频谱支撑域

为了分析场景的光场，首先需要理解不同类型场景的行为和光场中的场景元素。由于任何的复杂几何模型都可以通过一系列点的叠加来模拟，因此我们首先分析空间中的一点。图2给出了空间中一个点的顶视图，点的坐标为p=[px，py，pz]，从该点发出的一条光线穿过了两个参考平面。

图2 单一点光源的两平面参数化顶视图

从图2中可以清楚地看出，光场中的光线只有一部分会与点p相交。从图中的相似三角形中可以推导出与点p相交的所有光线的关系，s和u之间任意与点p相交的光线满足

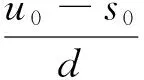
(1)

同样，t和v也满足类似的关系

(2)

请注意公式(1)和(2)分别描述了4D光场中的一个超平面[10]。只有这两个方程同时满足才能确定一条光线与空间的点相交。将这两个方程改写成矩阵的形式，则点p所占据的4D光线空间的子集可以描述成

(3)

公式(3)表示公式(1)和(2)所描述的两个超平面的交集。正如3D空间中两个平面的交集为一条线，4D空间中两个超平面的交集是一个平面。因此，公式(3)是4D空间中一个平面的方程。

为了描述点光源在光场中所对应平面中光线的值，我们首先假设场景中点p位置有一个全向点光源，该点发出的所有光都具有恒定值，因此该点在光场中对应的平面也具有恒定值。令该全向点光源的光场为l(s，t，u，v)，那么它的连续傅里叶变换为

L()=l(s，t，u，v)

·e-j(ss+tt+uu+vv)dsdtdudv

(4)

由于场景中只包含一个点p且该点位于参考平面u-v上，其中pz=d，因此该光场只包含了一个平面u=px，v=py。注意该平面是对齐的，平行于s-t平面，垂直于u-v平面。如果点p位置有一个全向点光源，那么光场平面的值将会是一个恒定值，因此整个光场沿着s和t将具有恒定值。这意味着沿着s和t的积分只在频域原点处有非零值，因此它的傅里叶变换可以改写成

L()=δ(s)δ(t)
l(s，t，u，v)e-j(uu+vv)dudv

(5)

这种简化等同于观察到的信号在s和t上是恒定的，因此它的频谱支撑域必须存在于这些轴上的零频率处。所得的频域信号的支撑域由公式(5)中的两个狄拉克函数定义。每个狄拉克函数定义了一个过原点的超平面，则它们的乘积定义了这两个超平面相交的平面。因此，空间中点p(其中pz=d)位置的一个全向点光源的频谱支撑域是一个过原点的平面。

上述观察所得可以推广到场景中任意深度处的一点，任意一个点光源对应光场中的一个平面，无论光源的深度是多少。而平面的朝向则随着光源深度变化而变化。这样，光场的频谱支撑域应该是上述过原点平面旋转后的版本。我们可以将新光场看作是pz=d的情况旋转后的版本：

l′(s，t，u，v)=l(R[s，t，u，v]T)

(6)

其中R是一个依赖于光源深度pz的4D旋转矩阵。傅里叶变换的性质告诉我们，空间域的旋转对应于频域的旋转，公式(6)在频域可以写成

L′()=L(RT)

(7)

因此，频域旋转后的光场的频谱支撑域是过原点平面旋转后的版本。

我们可以利用平面频谱支撑域的朝向和空间域光场平面的朝向之间的关系，从而避免了直接使用旋转矩阵R。在s-u平面，平面频谱支撑域垂直于空间域光场中的平面，即旋转了90°。在t-v平面，这一现象同样存在，两者结合在一起完整地描述了频谱支撑域的朝向。从公式(3)中可以发现，空间域平面在s-u和t-v坐标下的斜率都是d/pz。将这个平面分别在s-u和t-v坐标下旋转90°，即

(8)

这个方程描述了场景中任意深度位置的一个全向点光源的频谱支撑域，它的朝向只依赖于场景中点的深度pz。

2.2朗伯表面的频谱支撑域

2.1节分析了全向点光源的频谱支撑域，通过叠加的方法，可以将此结论扩展到表面。这需要将一个表面表示成一组表面元素的集合，比如多边形。当表面元素的数量非常巨大时，每一个表面元素变得无穷小，它的行为接近于空间中的一个点。

(a)

(b) 图3 平面频谱支撑域在(a)s-u平面和(b)t-v平面的投影

将这种方法应用于一个朗伯表面(Lambertian Surfaces)产生了一个特别简单的结果。一个朗伯表面的亮度与观看角度是无关的，因此可以看做是由无数个全向点光源组成的。这种处理不是完美的，因为它无法模拟遮挡，因此需要假设是场景中的一个朗伯表面且没有遮挡。在这个假设下，光场中朗伯表面的频谱支撑域可以看作是无数个点光源的频谱支撑域的叠加。

我们从最简单单一恒定深度表面开始，取一个平行于参考平面的表面，深度为pz。在该平面上所有的点光源都具有相同的深度，因此也具有相同的平面频谱支撑域，由公式(8)给出。由这些平面叠加而成的频谱支撑域本身就是个平面。这一观察所得对于包含任意数目的朗伯表面都成立，只要它们都具有相同的深度pz。图3(a)和(b)分别给出了场景中具有单一恒定深度的朗伯表面的频谱支撑域在s-u平面和t-v平面的投影。

3.FIR频率平面滤波器

在第二节我们证明了由位于单一恒定深度的朗伯表面组成的场景，它所产生的光场是由完全平行的、恒定值的平面组成。公式(8)描述了这样的光场的频谱支撑域，它是由两个4D超平面相交得到的平面，且在s-u平面和t-v平面上的投影都是一条斜率为的直线，其中pz是朗伯表面所在的深度。类似的，对于一个包含若干个位于不同离散深度上的朗伯表面的场景，它的光场包含了一组组平行平面，每一组平行平面的朝向取决于对应朗伯表面的深度。如果我们设计一个频率平面滤波器，只允许位于深度pz的朗伯表面通过，而去除或者模糊所有其他的场景元素，那么就可以实现深度滤波。

为了获得这样的4D频率平面通带，首先需要设计4D超平面滤波器，它可以通过2D直线滤波器来实现。由于直线没有宽度，理想的直线通带是无法实现的。在实际应用中，我们可以用宽度非常窄的频域矩形窗来近似直线通带，它的空间域表达式由公式(9)给出：

(9)

其中为直线的斜率，N为滤波器的阶数。可以看出，这样的2D直线滤波器具有偶对称系数，也就是说，具有线性相位特性。图4给出了这种2D直线滤波器的一个例子。

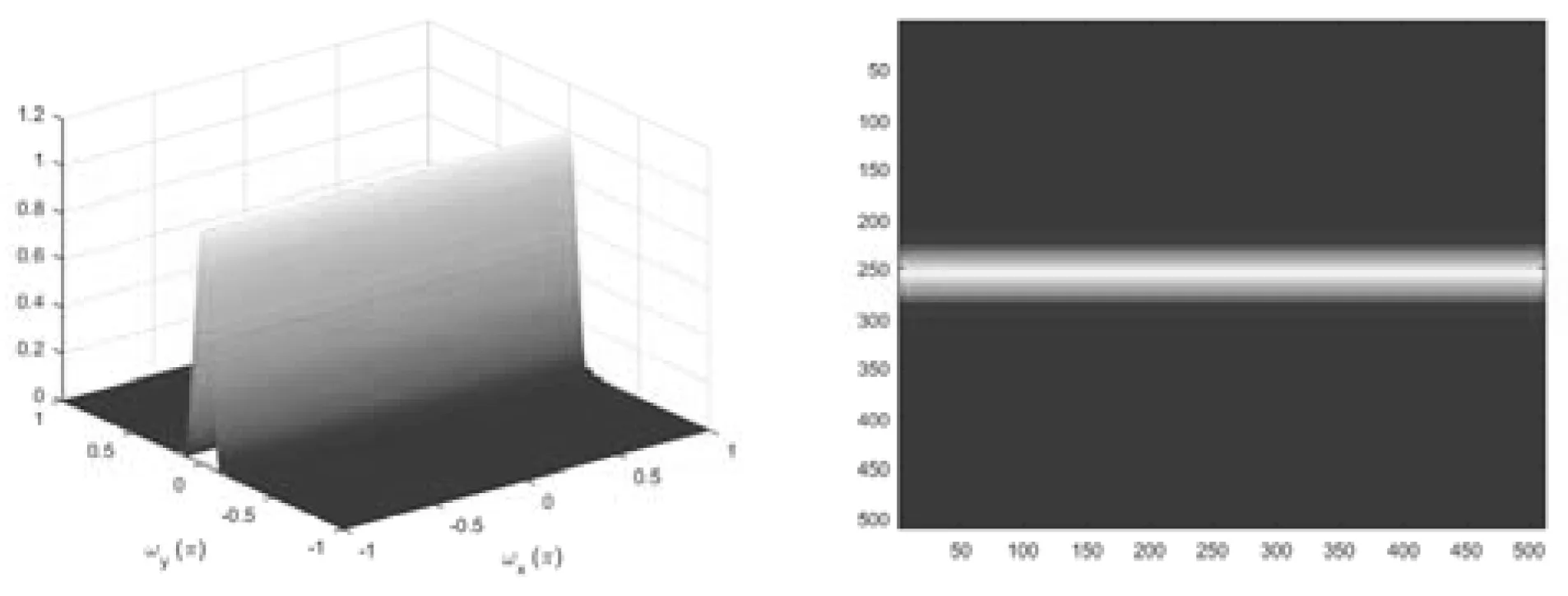
(a)频率响应 (b)频域顶视图图4 斜率为0的直线滤波器，阶数N=32，使用矩形窗

4D频率平面滤波器由两个不同平面的2D直线滤波器的卷积得到

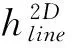
(10)

其中每个2D直线滤波器是由公式(9)得到的。这样的滤波器具有接近图3中所示的频率平面通带。由于两个2D直线滤波器都具有线性相位特性，因此所得的4D频率平面滤波器同样具有线性相位特性。在第四节我们将通过实验来验证它的深度滤波性能。

4 实验与分析

第三节提出的频率平面滤波器具有两个可以调节的参数：滤波器阶数和窗函数。具体的参数选择可以参考一维滤波器的窗函数设计法。需要注意的是，当光场规模较大时，滤波器的阶数极大影响处理时间，因此滤波器的阶数不宜过大。同时，还需要选择合适的窗函数，以避免或减小振铃效应。

斯坦福大学光场存档(StanfordLightFieldArchive)是一个公开的数据库，适用于评估光场滤波技术。图5展示了其中的“乐高骑士”(LegoKnights)光场的正视图。它包含了一个17×17网格上个的289张视图，每张视图的分辨率为1024×1024。光圈位置足够接近理想的网格，因此忽略其偏差导致的输出图像质量降低可以忽略不计。“乐高骑士”包含了不同深度的相对简单的几何物体，基面上由凸起组成的规律网格便于演示滤波器对于不同深度的选择性。因此我们选择“乐高骑士”光场作为实验对象。实验平台是一台笔记本电脑，使用了主频为2.3GHz的Inteli7-3610QM处理器，内存为8GBytes。测试程序运行在Matlab上，没有使用分块或其他加速算法。为了降低存储需求和处理时间，光场中的视图被下采样到512×512像素。

图5 输入光场“乐高骑士”的正视图

为了验证频率平面滤波器的深度滤波性能，我们设计了两个尺寸为17×17×17×17的空间域频率平面滤波器，斜率分别为0.6和2.5，使用了β=3的凯泽窗。分别将它们应用到输入光场，图6给出了深度滤波的输出光场的正视图。可以看出，两个频率平面滤波器分别保留了中间小人和背景，而将其它深度范围的场景元素模糊掉。大致的通带范围可以根据基面上凸起的清晰程度判断。

值得注意的是，有一部分想要的信号也被轻微模糊了，比如图6(a)中间小人头盔的亮斑附近和(b)中背景。这是因为“乐高骑士”中包含了轻微的镜面反射，这会导致频谱的“拉伸”[11]，并被滤波器衰减掉一部分。另一个可能的原因是，光场处理中假设相机是一个理想的针孔相机，从而导致光场测量出现误差，引起不必要的模糊。

(a)斜率为0.6

(b)斜率为2.5图6 空间域频率平面滤波器输出光场的正视图

作为对比，图7展示了文献[12]中提出的频率平面IIR滤波器的深度选择性能，其中(a)中使用的滤波器斜率为0.6，(b)中使用的滤波器斜率为2.5，和前面例子相同。对比图6和7，可以看出，本文所提出的频域频率平面滤波器的通带要比文献[12]中的方法要窄，而且没有出现振铃效应，而7(b)中的背景上可以观察到很明显的振铃效应。因此，本文提出的方法整体上要优于文献[12]中的方法，而且本方法的设计可以借鉴设计一维滤波器的窗函数法来调整参数，设计简单灵活，同时具有线性相位特性。

(a)斜率为0.6

(b)斜率为2.5 图7 文献[12]中提出的频率平面IIR滤波器输出光场的正视图

5 结论

本文提出了一种4DFIR频率平面滤波器，它的通带形状近似一个过原点的平面，可以提取场景中具有单一恒定深度的表面。该滤波器简单地使用窗函数法实现，参数调整简单灵活，可以借鉴一维滤波器的设计方法。与文献[12]中的频域方法相比，不仅设计更加简单灵活，而且在窄过渡带的情况下不会出现振铃效应。此外，本文提出的频率平面滤波器具有线性相位特性，具有一定的应用价值。

[1]MLevoy，PHanrahan.Lightfieldrendering[J].SIGGRAPH，ACM，1996，31-42.

[2]SJGortler，RGrzeszczuk，RSzeliski，MFCohen.Thelumigraph[J].ProcSIGGRAPH，1996，43-54.

[3]EHAdelson，JRBergen.Theplenopticfunctionandtheelementsofearlyvision[J].Computationalmodelsofvisualprocessing，1991，91(1)：3-20.

[4]CZhang.Onsamplingofimage-basedrenderingdata[D].PhDthesis，DepartmentofElectricalandComputerEngineering，CarnegieMellonUniversity，2004.

[5]DGDansereau，LTBruton.A4Dfrequency-planarIIRfilteranditsapplicationtolightfieldprocessing[J].IntlSymposiumonCircuitsandSystems(ISCAS)，IEEE，2003(4)：476-479.

[6]DGDansereau，LTBruton.A4-Ddual-fanfilterbankfordepthfilteringinlightfields[J].IEEETransactionsonSignalProcessing，2007，55(2)：542-549.

[7]DGDansereau，DLBongiorno，OPizarro，SBWilliams.Lightfieldimagedenoisingusingalinear4Dfrequency-hyperfanall-in-focusfilter[J].ProceedingsSPIEComputationalImagingXI，Feb，2013，86570P.

[8]DGDansereau，OPizarro，SBWilliams.LinearVolumetricFocusforLightFieldCameras[J].ACMTransGraph34，2(2015)：15-1.

[9]ChamiraUSEdussooriya，DonaldGDansereau，LenTBruton，PanajotisAgathoklis.Five-DimensionalDepth-VelocityFilteringforEnhancingMovingObjectsinLightFieldVideos[J].IEEETransSignalProcess，2015，63(8)：2151-2163.

[10]SLang.CalculusofSeveralVariables[J].SpringerVerlag，January，1995.

[11]CZhang，TChen.Lightfieldsampling[J].Synthesislecturesonimage，videoandmultimediaprocessing2，1(2006)：1-102.

[12]Dansereau，DonaldGilbert.Plenopticsignalprocessingforrobustvisioninfieldrobotics[D].PhDdissertation，TheUniversityofSydney，2014.

(责任编辑：宋金宝)

A Closed Form Sound Source Location Solution Using Range Differences of Arrival or Gain Ratios of Arrival Video Frames

FANG Li，YE Long，ZHONG Wei，ZHANG Qin

(Key Lab of Media Audio & Video of Ministry of Education，Communication University of China，Beijing 100024，China)

A 4D FIR frequency planar filter with a passband that approximated a 4D plane is proposed.The proposed filter is simply designed by window method，and possesses linear-phase property.Therefore，it is efficient to process light field.Theoretical deduction and experimental results show that a light field containing Lambertian surfaces with no occlusions can be selectively filtered for depth using the proposed filter.

four-dimensional filter；light field；scene analysis；window method；linear phase

2017-05-01

方力(1989-)，男(汉族)，河南西峡人，中国传媒大学博士研究生.E-mail：lifang8902@gmail.com

TN

A

1673-4793(2017)04-0028-06