浅析几何直观：寻找解决问题的“天平”

陈沁

摘 要：新课程教育背景下，教师要创新教学方法，从学生学习兴趣入手，降低学习难度，为学生后续学习奠定基础。对此，通过《解决问题的策略：假设》案例教学，对几何直观问题的解决进行简要分析。

关键词：几何直观；解决问题；天平模型；解决方法

天平模型贯穿教学始终，是教学形式的一种创新，对学生数学学习具有帮助性作用，同时也能为学生数学学习积累经验，这种经验对学生问题的解决具有帮助性作用。引导学生在头脑中构建天平模型，激发学习兴趣，进而解决有关问题。

一、教材设计

以某教材《解决问题的策略：假设》为案例。教材设计2道习题，例题1：倍数关系假设：小美将960毫升的水倒进6个小杯、2个大杯中，杯全部被倒满。小杯容量是大杯容量的，求小杯、大杯容量各有多少毫升？例题2：相差关系假设：3个大盒与4个小盒中装球，全部装满球数量为100个。大盒比小盒多8个球，问：大盒小盒中各有多少球？

二、教學分析

在教学过程中，首先对学生进行测试。结果显示：例题1掌握率在61%，例题2掌握率在20%。针对“两种不同量的假设”学生在之前学习中有所涉及，例如异分母分数加减等问题。其实，解决问题的关键在于数量相等关系，“假设”方法主要是为等量关系奠定基础。所以，在教学中，怎样帮助学生建立假设后的等量，成为问题解决的核心。

三、设计目标

数学是一门偏理性学科，是数与形的结合。据调查显示：人们在感知能力上，对于“形”的表现较为深刻。在本次教学中，关于“数”的有关知识概念较为抽象化，因此，怎样通过“形”进行教学，简化学生学习，成为教学重要的研究课题。在方程教学中，借助天平简化学习，天平则成为方程解决的关键。但是，天平是否在等量关系解决中构成模型。笔者认为：数量相等关系模型，就是解决问题的核心。所以，可以通过几何直观引导数量相等关系，进行模型构建。另一方面，数学教学不仅是知识的传递，更多的是为学生后续数学探究奠定基础。而通过这样设计引导，能够帮助学生找到问题的切入点，简化数学知识，让学生更好地认识数学，为今后发展奠定基础。

所以，笔者将例题1、2进行了整合，通过苹果与梨的重量导入天平教学模型，以更好地形成比较，将抽象化的知识点形象化，帮助学生更好地理解。

四、教学过程

教学1：应用天平，感悟数量关系。首先，教师进行图片展示（如图一），并提出图中的天平代表什么？学生经过思考得出：4个苹果的重量为600克，进而得出一个苹果的重量。在这一过程中，让学生了解一种量建立相等数量关系时，我们可以直接得到答案，为后续“假设”教学奠定基础。通过图形的形式更好地阐述数量关系，便于理解。

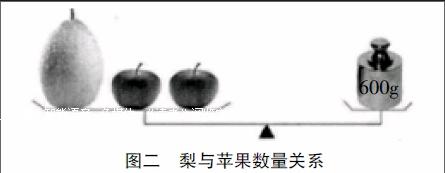
教学2：掌握变化的数量关系。教师将图形（如图二）呈现在学生眼前，进而学生得出：一个梨和两个苹果的重量等于600克；教师提问：我们在计算苹果与梨的重量时，是否可以按照上述计算方法，将总重量除以3？学生回答：梨和苹果重量不一，不能相除。那么，我们怎样在原有问题下，将梨变为苹果？学生经过思考回答：补充条件，梨的重量是苹果的2倍（倍数关系）。也有学生提出：梨比苹果重150克（相差关系）。教师提问：同学们，能够找到假设后的天平吗？学生回答：4个苹果重量为600克。2个梨重量为600克。

这样的假设，成为问题方法研究的基础，进而让学生懂得“假设的意义”。

让学生了解问题特点。而如何假设则成为方法难点。在教学过程中，不断地引导、鼓励学生进行多样化的假设，通过不同水果将其假设为同一种水果。

教学3：引入天平，深化数量关系。如果我们设置：梨比苹果重150克，该问题是否可以通过假设解答。教师引导学生进行小组研究，得出：将梨换做苹果。这时，教师进行教学演示，发现天平两边不平衡，让学生明白数量关系相关知识点，因为将梨换做苹果后，重量减少了150克，而右边重量不变。如果想让天平平衡我们还需要在右边减150克。

通过相差关系进行问题假设，究其原因，假设后总量发生了变化，原有等量关系不平衡，进而需要重新进行等量假设；第二，假设后数量关系更为繁琐，而知识点又具有一定抽象性，需要引导学生找到切入点，而通过天平模型进行假设说明，简化学生理解，进而让学生掌握数量关系。

通过此次教学实践，天平教学方法效果良好，学生参与性较高，降低了学生的学习难度，对教学起到了帮助性作用。笔者分别从：教材设计—教学分析—设计目标—教学过程进行分析，希望对教学有所帮助。

参考文献：

[1]丁占海.读“图”教学：让几何直观自然地生长[J].教学与管理，2013（35）.

[2]潘天平.几何直观在解决一次函数实际问题中的应用探究[J].教育实践与研究，2014（8）.