基于VMD与分层极限学习机的滚动轴承故障诊断方法研究*

秦波，孙国栋，王建国(内蒙古科技大学机械工程学院，内蒙古包头014010)

基于VMD与分层极限学习机的滚动轴承故障诊断方法研究*

秦波，孙国栋，王建国
(内蒙古科技大学机械工程学院，内蒙古包头014010)

针对滚动轴承信号的不规则特性，致使信号故障特征难提取及难以辨识的问题，为实现滚动轴承故障的智能诊断，提出基于VMD排列熵与分层极限学习机的滚动轴承故障诊断方法。首先将测得振动信号进行变分模态分解(Variational Mode Decomposition，VMD)，利用排列熵进一步提取各模态特征组成高维特征向量集;其次利用自动编码器(Automatic Encoder，AE)对极限学习机的隐含层进行分层，且使隐含层节点的输入权值和阈值满足正交条件;最后将构建的特征向量作为H-ELM算法的输入，通过训练建立H-ELM滚动轴承故障分类模型。实验结果表明:H-ELM滚动轴承故障分类模型比SVM、ELM故障分类模型具有更高的精度、更强的稳定性。

滚动轴承;变分模态分解;自动编码器;极限学习机

0 引言

滚动轴承工作状态正常与否直接关系着机械设备乃至整个系统的运行状态，因此需要对滚动轴承实施状态嫉测和故障诊断［1］。但是由于加工工艺、工作环境等原因造成其信号非线性、非平稳。而传统的时频域分析方法大多针对线性、稳态信号的分析，因此难以精确、稳定地识别轴承的故障［2］。

目前，为了精确、稳定地识别轴承的故障类型，国内外科研工作者提出了一系列的方法。文献［3］提出一种GA和LM组合优化BP神经网络的故障诊断方法，实验结果表明，组合优化后的BP神经网络具有更高的诊断效率和精度。钟小凤等［4］通过主成分分析方法(PCA)对滚动轴承的故障特征进行特征提取，将提取后的特征向量输入到最小二乘支持向量机故障诊断模型中实现滚动轴承的故障诊断。虽然上述方法具有一定的有效性，但BP神经网络学习时间较长、易造成欠拟合和陷入局部最优解等缺陷。SVM支持向量机与BP相比具有了更强的稳定性，并能确保局部和全局最优解完全相同。但SVM模型的低稀疏度使其在处理大样本数据时训练时间大幅度增加。Huang［5］提出的极限学习机具有训练时间短、泛化能力强且适合多维度数据训练，但其隐含层节点的输入权值和阈值随机生成，且只有一个隐含层，致使模型的精度低，鲁棒性差。2013年王杰［6］使用粒子群算法选择最优的输入权值矩阵和隐含层偏差，从而计算出输出权值矩阵相比于ELM算法，粒子群极限学习机算法具有较高的精度，但容易陷入局部极小值而找不到全局最优解。黄勤芳等［7］结合小波分析理论对滚动轴承振动信号进行故障特征提取，引入结构风险最小化原理对极限学习机进行改进及优化，构建了滚动轴承振动故障诊断模型。仿真结果表明，故障诊断模型的分类准确率有了进一步提高。但所要调节的参数增加，需要多次训练，降低了效率。

针对上述问题，提出基于VMD排列熵与分层极限学习机的滚动轴承故障诊断方法。先对测得振动信号进行变分模态分解并提取排列熵组成高维特征向量集;而后利用自动编码器对极限学习机的隐含层进行分层，使隐含层节点的输入权值和阈值满足正交条件;最后将高维特征向量集作为H-ELM算法的输入，通过训练建立H-ELM滚动轴承故障分类模型。

1.1 变分模态分解

VMD是2014年K.Dragomiretskiy［8］等提出的一种新的信号处理方法，核心思想为变分问题。VMD的分解过程即变分问题的求解过程，包括构造和求解两部分，涉及了3个重要概念:经典维纳滤波、希尔伯特变换和频率混合。

(1)变分问题的构造

变分问题是将输入信号f(x)分解为n个摸态函数Un(t)，假设每个“模态”的有限带宽具有中心频率ωn，使每个模态的估计带宽和最小。约束条件为各模态之和等于输入信号f(x)，具体构造步骤如下:

①通过Hilbert变换，得到每个模态函数Un(t)的解析信号。

②对各模态的解析信号混合预估中心频率，将每个模态的频谱移动到基频带上。

③使用解调信号的H高斯平滑，估计各模态信号带宽，即梯度的二范数的平方。由此受约束的变分问题如下:

其中，t表示对t求偏导数，δ(t)为冲击函数。

(2)变分问题的求解

通过引入拉格朗日乘子γ(t)和二次惩罚因子α得到式(1)的增广拉格朗日函数。

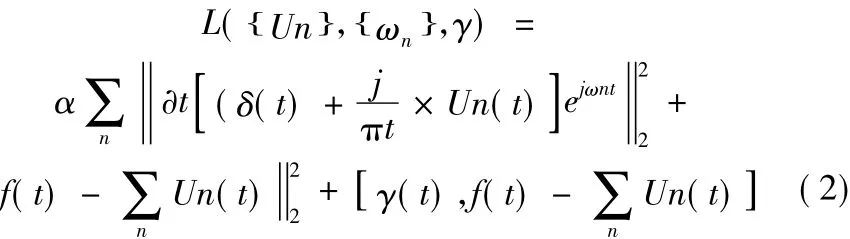
利用交替方向乘子法(ADMM)［9］求解上式的迭代，迭代次数为k收敛条件为:

然后利用傅里叶等距变换，将迭代后的结果转变到频域上进行更新，解得:

VMD算法步骤:

②根据式(4)～式(6)更新Un，ωn，γ;

③根据收敛条件(3)判断结果是否满足，满足就停止计算，否则返回步骤②。

1.2 分层极限学习机

在极限学习机算法中，使输入样本数据等于输出样本数据，这样ELM就能够无监督学习;并使随机生成的隐含层节点的权值α和阈值b都满足正交条件，这就是ELM自动编码器的基础［10］，下面叫做ELM-AE。

在ELM-AE中生成的正交隐含层参数把输入样本数据映射到高维空间中，如由Johnson-Lindenstrauss引理［11］得到如下计算公式:

其中:α=［α1，α2，…，αN］是连接输入层和隐含层节点的正交权值，b=［b1，b2，…，bN］是正交的隐含层节点阈值。ELM-AE的输出权值β使特征空间到输入数据的学习转换，根据以下公式计算输出权值β:

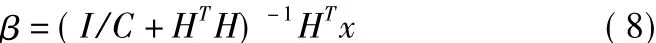
H-ELM是在ELM-AE的基础上进行堆叠而形成的一个分层神经网络。H-ELM不需要微调，其隐含层参数通过ELM-AE进行初始化，使得参数满足正交条件，其网络结构如图1所示:圆圈表示神经元节点，每一层的输出会作为下一层的输入依次进行，直到达到满意的精度和合适的测试时间，最后一个隐含层与输出层的输出矩阵用最小二乘法进行计算。

图1 H-ELM的网络结构

H-ELM算法步骤如下:

①给定训练样本S={(xj，tj)|xj∈Rn，tj∈Rm，j= 1，2，…，N}隐含层激活函数为g(x);

②设置好H-ELM的网络结构，使得x=y，利用极限学习机自动编码器对其隐含层进行分层，使得参数满足正交条件;

③计算隐含层输出矩阵H;

④利用式(8)计算输出权重β;

⑤当1≤i≤y－1时，循环步骤③、④，计算第i层隐含层的输出矩阵;

⑥当i=y时，利用最小二乘方法计算最后一层的隐含层输出矩阵。

2 实验验证

借助LMS Test.Lab数据采集仪与美国Spectra Quest公司机械故障综合模拟试验台搭建数据采集系统(图2)来验证所提方法的有效性。该实验台由电机、变频器、联轴器与转子等组成。加速度传感器分别布置在靠近电机轴承座的水平径向、垂直径向和水平轴向三个方向上采集信号，所采集的振动信号经由LMS Test.Lab数据采集仪接入计算机进行分析、保存。滚动轴承的转速为2100r/min，采样频率为5120Hz，数据的采样点数为5120个。

图2 基于LMS的机械故障综合模拟试验台

通过依次对图2中轴承的正常、外圈故障、内圈故障、和滚动体故障4种状态件进行更换，并采集上述四种状态下的振动加速度信号，分别获得每种状态30组数据，每组数据包含5120个采样点。抽取每种状态20组作为训练样本，余下10组作为测试样本。

首先对训练样本和测试样本数据进行VMD分解得到其模态U分量，其中，从K为5开始，出现了中心频率相近的模态，本文认为出现了过分解，因此，模态数选为4，如图3内圈故障的模态U分量所示。然后求取4种状态信号模态U分量的排列熵值，组成特征向量作为H-ELM滚动轴承故障诊断模型的输入。表1为测试样本的四种状态下的部分排列熵值。

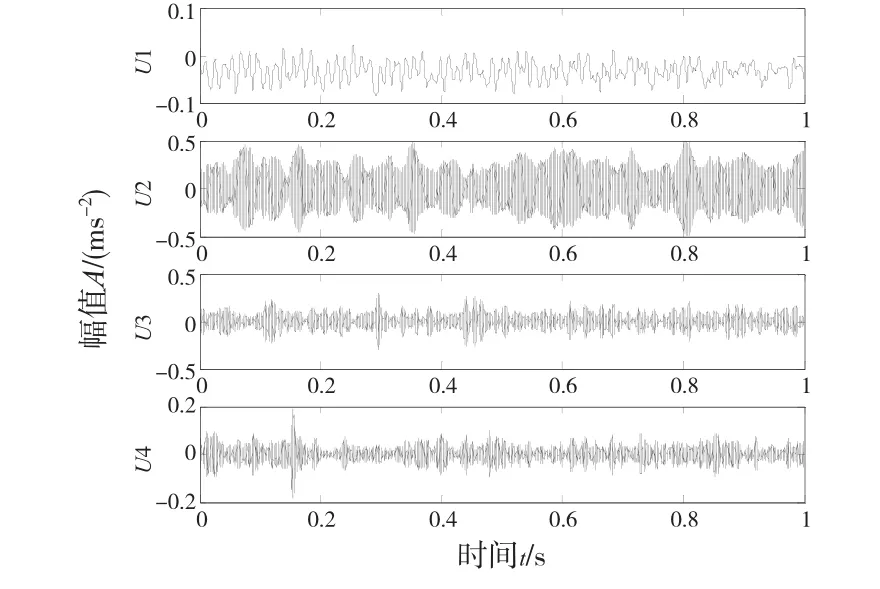
图3 内圈故障的模态U分量

表1 滚动轴承四种排列熵值特征向量

为验证所提方法的优越性。分别将表1中的特征向量输入到SVM、ELM与H-ELM中进行训练与测试，其中SVM中惩罚参数C与核宽度系数σ人为设为2与0.2;H-ELM中首先确定各多层极限学习机的层数。先从测试时间来看，H-ELM模型进行轴承故障识别，当网络结构超过5层时，测试时间迅速增长，效率偏低，因此舍弃超过5层以上的网络结构。再从测试正确率来看，4层要比3层的测试正确率要高。因此HELM模型的网络结构选择4层。利用核函数自适应确定各层的神经元节点数口分别为41，37，100，2。

三种算法的测试样本分类结果分别如图4～图6。从图4中看出SVM对于轴承故障分类精度达到90% (36/40);从图5中看出ELM对于轴承故障分类精度达到87.5%(35/40);从图6中看出，H-ELM对于轴承故障分类精度达到100%(40/40)。上述四种方法的对比结果如表2所示。

图4 SVM的测试样本分类结果

图5 ELM的测试样本分类结果

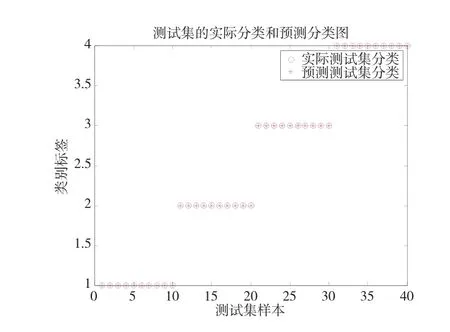
图6 H-ELM的测试样本分类结果

表2 SVM、ELM、H-ELM三种诊断模型性能比较

3 结束语

针对滚动轴承振动信号的不规则性和复杂性，导致轴承状态难以有效识别的问题，提出基于分层核极限学习机的滚动轴承故障诊断方法。VMD作为一种新的方法用来分解振动信号得到模态分量，本质是一组白适应维纳滤波器，各模态携带着不同频率的滚动轴承故障信息，对其提取排列熵值能够更精确地表达故障特征。然后利用提取的各模态分量的排列熵作为本模型的输入，进行轴承故障的分类和识别。通过实验结果分析，得出所用方法对比SVM、ELM具有良好的效果以及更高的模型的精度与鲁棒性，在轴承故障诊断领域有广泛的应用前景。

［1］秦波，刘永亮，王建国，等.基于小波包与奇异值分解的GA-SVM滚动轴承故障诊断方法研究［J］.机械设计与制造，2016(6):38－42.

［2］张沛朋，郭飞燕.基于PCA-SVM的滚动轴承故障诊断研究［J］.组合机床与自动化加工技术，2015(11):88－90.

［3］钟小倩，马文科，宋萌萌.基于GA和LM组合优化BP神经网络的滚动轴承故障诊断方法［J］.组合机床与自动化加工技术，2014(12):91－95.

［4］钟小凤，贺德强，苗剑.基于PCA-LSSVM的机车走行部滚动轴承故障诊断研究［J］.广西大学学报(自然科学版)，2014，39(2):328－333.

［5］G B Huang，Q Y Zhu，C K Siew.Extreme learning machineaheory and applications［J］.Neurocom-puling，2006，70:489－501.

［6］王杰，毕浩洋.一种基于粒子群优化的极限学习机［J］.郑州大学学报(理学版)，2013，45(1):100－104.

［7］黄勤芳，程艳，陈伟珍.改进极限学习机在滚动轴承振动故障诊断中的应用［J］.机械设计与制造，2016(1):80－83，87.

［8］Dragomiretskiy K，Zosso D.Variational mode decomposition［J］.IEEE Transactions on Signal Processing，2014，62 (3):531－544.

［9］Liu H，Song B，Qin H.An adaptive-ADMM algorithm with support and signal value detection for compressed sensing［J］.IEEE Signal Processing Letters，2013，20(4):315－318.

［10］WIDROW B，GREENBLATT A，KIM Y，et al.The No-Prop algorithm:a new learning algorithm for multilayer neural networks［J］.Neural Networks，2013，37:182－188.

［11］JOIINSON W B，LINDENSSTRAUSS J，SCHECHTMAN G.Extensions of Lipschitz maps into Banach space［J］.Israel，Journal of Mathematics，1986，54(2):129－138.

(编辑李秀敏)

Research on Rolling Bearing Fault Diagnosis Method Based on VMD and Hierarchical Extreme Learning Machine

QIN Bo，SUN Guo-dong，WANG Jian-guo
(School of Mechanical Engineering，Inner Mongolia University of Science＆Technology，Baotou Inner Mongolia 014010，China)

According to the irregularity characteristics of the rolling bearing signals，cause the bearing condition is difficult to identify，and the hierarchical extreme learning machine faultdiagnosis modelis proposed.Firstly，the measured vibration signals are decomposed into variational mode decomposition，using the permutation entropy to extractthe features of each modelto form a high dimensionalfeature vector set;Secondly，the hidden layer of the extreme learning machine is layered by using automatic encoder，and the input value and threshold value of the hidden layer nodes are satisfied;Finally，the combined feature vector is used as the inputof the algorithm，and the faultclassification modelof the rolling bearing of the hierarchical extreme learning machine is established.The experimental results show that the H-ELM rolling bearing fault classification model is better than ELM，and the SVM fault classification model has higher accuracy and stronger stability.

rolling bearing;variationalmode decomposition;automatic encoder;extreme learning machine

TH165;TG506

A

1001－2265(2017)04－0107－04

10.13462/j.cnki.mmtamt.2017.04.027

2016－08－02;

2016－09－01

国家自然科学基金(51565046);内蒙古自然科学基金(2015MS0512);内蒙古科技大学创新基金(2015QDL12)

秦波(1980—)男，河南南阳人，内蒙古科技大学讲师，工学硕士，研究方向为复杂工业过程建模、优化及故障诊断，(E－mail)nkdqb@ 163.com;通讯作者:孙国栋(1992—)，男，山东聊城人，内蒙古科技大学硕士研究生，研究方向为机电系统智能诊断，(E－mail)sgdyl121115@163.com。