基于改进遗传算法的自动组卷问题研究

梁树杰

（广东茂名幼儿师范专科学校，广东 茂名 525200）

基于改进遗传算法的自动组卷问题研究

梁树杰

（广东茂名幼儿师范专科学校，广东 茂名 525200）

利用标准传统遗传算法进行自动组卷，有收敛速度慢和未成熟收敛的缺点。本文运用遗传算法的原理和分段二进制编码策略，得到改进遗传算法。实验结果表明，利用改进遗传算法进行解自动组卷，能够明显地提高组卷成功率和减少组卷时间。

遗传算法；改进；效率；时间

0 引言

随着计算机和互联网的发展，网上考试系统得到了广泛的应用。自动组卷技术是网上考试系统的重要技术。应运用高效、科学的算法，才能有效地解决自动组卷问题，基于改进遗传算法的自动组卷技术对于完善网上考试系统具有重要的作用。

1 自动组卷问题分析

一般来说，用户对最终生成的试卷都有一定的要求，如试卷试题的难度系数、题型分布、知识覆盖面和答题时间等。从数学方法来看，在组卷之前，应建立组卷控制指标对应的状态空间。用an表示控制指标，用m表示试卷试题数量，用S表示试卷矩阵。在矩阵S中，各行由试题难度系数、知识覆盖面等控制指标状态，对这些属性指标用二进制编码表示；各列为试题控制指标的全部取值。在求解组卷问题时，将矩阵S作为目标状态矩阵，并用S、D、Q、Z、T分别表示试卷的总分、难度、题型、知识范围和答题时间，并满足如下约束条件：

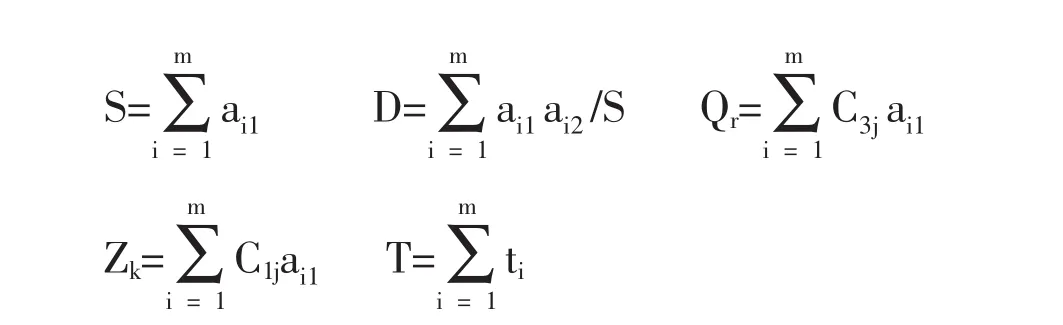
2 标准遗传算法

遗传算法是对决策变量编码，并把它作为运算对象来解决问题的一种算法。在运用遗传算法时，无需获取问题领域的具体信息，不受搜索空间是否可微或连续的限制。运用遗传算法解决问题时，必须制定编码方案和确定适应函数，并利用适应度值度量解的质量。在问题的演绎过程中，可以根据解的适应值进行选择[1]。不仅要确定函数还要确定选择策略、选择控制参数、算子设计。通过制定优胜劣汰选择机制，使有较好适应值的解的存活概率更高；选择不同遗传操作的概率、群规模、算法执行最大代数，以及有关的辅助控制参数；选择再生、杂交、变异等方法。并确定算法的终止准则[2]。根据用户建立约束条件，从试题库中搜索与特征参数相匹配的试题。

3 基于改进遗传算法的自动组卷问题求解

运用标准遗传算法自动求解组卷问题，要出现收敛速度慢、早熟等问题。所以，还应对标准遗传算法进行改进，以更好地求解组卷问题。

3.1 制定编码方案

可以采用分段二进制编码策略改进标准遗传算法。将题库划分成若干段，每段表示一种题型。结合各题型的数量确定各段长度，然后分别对各段进行二进制编码[3]。根据试题库中试题的数量，确定编码长度。假设试题库的试题数量为n，有 a、b、c 三种题型， 各段长度分别用 k1、k2、k3表示 ， 则 n={[a1，a2，...，ak1]， [b1，b2，...，bk2],[c1，c2，...，ck3]}，且满足

运用二段制编码，能够缩小组卷搜索空间，并能提高组卷问题求解效率；也能满足试卷的题型及其试题数量要求[4]。在初始化阶段，组卷中各题型的分数保持相等，以满足试卷的总分要求，并降低试卷的冗余度，提高组卷效率。

3.2 适应度函数定义

3.3 遗传算子设计

还应做好选择算子、变异算子和交叉算子的设计工作。首先，在设计选择算子时，把最佳个体保存法和适应度比例选择法结合起来，以选择最佳的个体。在此基础上，直接复制个体，并直接带入下一代[6]。在选择其余的个体时，要使用比例选择法，以确保个体被选中的概率与适应度保持一定的比例。个体被选中的概率用表示。在设计交叉算子时，应结合编码策略，使用单点交叉法，即在段内进行交叉。在设计变异算子时，利用局部搜索能力，并将其作为组卷问题求解的辅助算法[7]。经过初始化后，群体能满足题分和题型的比例要求。还应采用同题型内两点变异法，使题型在所属编码段实现变异。

3.4 控制参数确定

在确定控制参数时，还要确定变异概率和交叉概率。这两个参数对遗传算法具有重要的影响。在标准遗传算法中这两个参数基本上是固定值。为搜索全局最优解，还应确定适应度标准，在适应度发生变化时，使交叉概率和变异概率随之改变。还应确定最优解搜索的终止条件，使种群在出现用户满意试卷后停止搜索最优解[8]。还应规定最大适应度值的变化率，当前后两代最大适应度值的变化小于这一数值，之后不再发生显著的进化效果，结束群体进化过程。

3.4 改进遗传算法的实验验证

下面通过实验验证改进遗传算解决自动组卷问题的效果。从有600道题的试题库选取试题组卷，包括单选题、多选题、判断题、填空题、简答题等五种题型，试卷总分100分，各题型分数固定。在选题时，应满足题型约束，选择各章节的试题分值与要求之间的误差不超过±2分，且难度分值误差也不超过±2分。首次实验的群体规模的变异概率与交叉概率分别设为0.01和0.6。实验结果如表1所示。

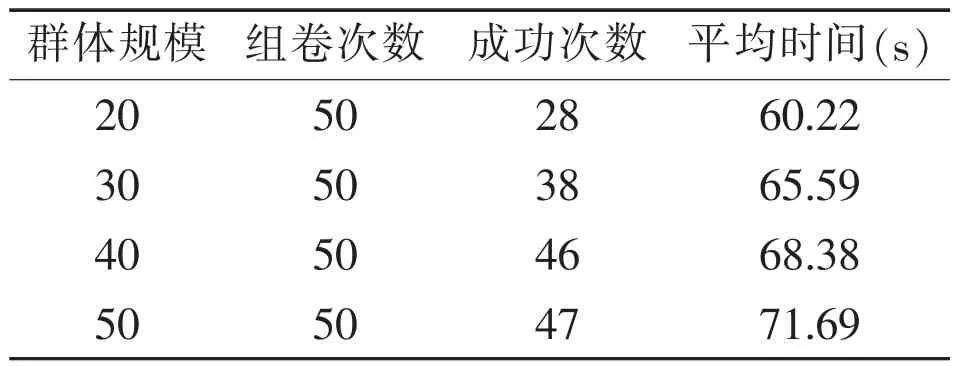
表1 群体规模实验结果

分析实验结果发现，在群体规模较小的情况下，只有少量试题参与组卷，只能在较小的空间范围查找最优解，获得有效试卷的概率较小；随着群体规模逐渐扩大，获得有效试卷的次数逐步提高。由此可见，群体规模对算法的收敛性产生较大影响。群体规模设为40和50时，获得的组卷效果差别并不明显。因此可以说明，在群体规模达到一定数值后，群体规模变化对算法的收敛性影响较少。群体规模变化对程序运行时间影响明显。

为了分析改进遗传算法中参数的灵敏性，进行第二次实验。建立的初始群的试题类型、分数分布达到组卷要求。在利用改进遗传算法进行组卷问题求解时，还应考虑试题难度系数、组卷时间和试题章节分布条件。在分析某项约束条件时，应把其他误差对应的权重设定为零，以排除其他因素的干扰。实验结果如表2所示。

表2 参数灵敏度实验结果

从表2的实验分析结果发现，改进的遗传算法对试题章节分布影响最大。如果消除这个影响，能明显提高改进遗传算法的成功率，明显缩短组卷问题求解的时间。因此，应适当降低各章节试题分布的误差权重。

按照组卷要求，采用标准遗传算法和改进遗传算法分别进行实验，并比较实验结果，结果如表3所示。实验结果表明，采用改进遗传算法能够提高组卷成功率，明显减少平均组卷时间。因此，采用改进遗传算法能更好地解决自动组卷问题。

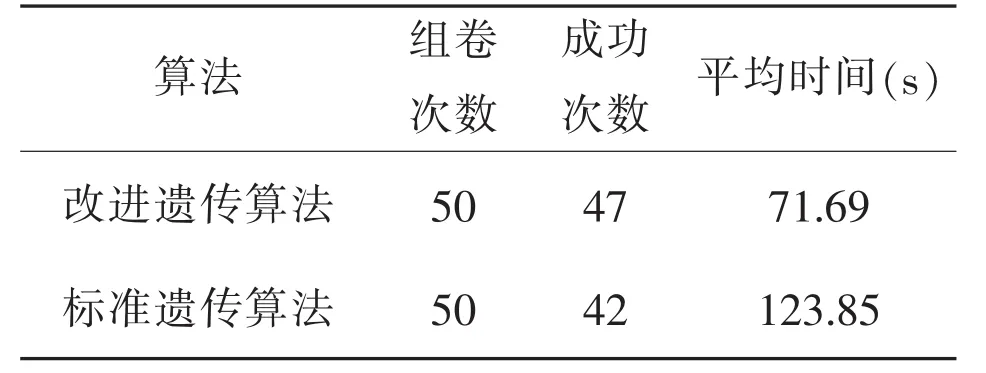
表3 标准进遗传算法和改进进遗传算法组卷实验结果比较

4 结论

通过研究发现，标准传统遗传算法不能满足快速组卷的需求。利用遗传算法原理和分段二进制策略获得的改进遗传算法，能减少组卷迭代次数，提高组卷成功率，减少组卷时间。因此改进遗传算法能提高在线考试系统自动组卷的效率。

[1]陈国彬,张广泉.基于改进遗传算法的快速自动组卷算法研究[J].计算机应用研究,2015（10）:2996-2998.

[2]席卫文，张春辉，王飞，等.一种基于改进遗传算法的医学题库自动组卷设计与实现[J].中国医学物理学杂志,2016（8）:861-864.

[3]宋芝兰.基于遗传算法自动组卷问题的设计研究[J].商场现代化，2011（4）:9-10.

[4]樊光辉,韩宝强.改进遗传算法在自动组卷中的应用[J].软件导刊，2011（11）:74-76.

[5]杨世达,金敏,梅磊.面向自动组卷问题的改进类电磁算法[J].计算机工程与应用，2011（35）:51-53.

[6]黄小明,刘长安.改进遗传算法在自动组卷系统中的应用[J].科学技术与工程，2010（8）:1999-2002.

[7]王凤蕊,王文宏,潘全科等.解决智能组卷问题的和声搜索算法研究[J].计算机仿真,2010（3）:298-301.

[8]宋秋莲.改进型遗传算法在自动组卷系统中的应用研究[J].计算机光盘软件与应用,2013（24）:117-118.

责任编辑仇大勇

Problems of the Automatic Test Paper Based on the Improved Genetic Algorithm

LIANG Shujie
(Guangdong Preschool Normal College in Maoming,Maoming Guangdong 525200,China)

The standard traditional genetic algorithm for automatic test paper has the disadvantages of slow and premature convergence.The genetic algorithm is improved by applying its principle and the segmented binary encoding strategy in this paper.The experimental results show that the improved genetic algorithm for automatic test paper can significantly improve the success rate of test and reduce the test time.

genetic algorithm;improvement;efficiency;time

TP18

A

1674－5787（2017）02－0149－03

10.13887/j.cnki.jccee.2017（2）.39

2017-03-02

本文系全国教育信息化项目“网络环境下教师继续教育研修模式的研究”(项目编号：1436219964)的研究成果之一。

梁树杰（1981—），男，广东高州人，硕士，广东茂名幼儿师范专科学校讲师，研究方向：计算机应用技术。