拥挤收费下出行者出行时段选择影响分析

岳贤飞，傅白白，武可心

(1.山东建筑大学 交通工程学院，山东 济南 250101；2.山东建筑大学交通研究所，山东 济南 250101；3.山东建筑大学建筑城规学院，山东 济南 250101)



【交通运输】

拥挤收费下出行者出行时段选择影响分析

岳贤飞1,2，傅白白2,3*，武可心1

(1.山东建筑大学 交通工程学院，山东 济南 250101；2.山东建筑大学交通研究所，山东 济南 250101；3.山东建筑大学建筑城规学院，山东 济南 250101)

城市机动车保有量持续增加，使得道路拥挤问题日益严峻。通过拥挤收费增加当前道路资源的利用率是解决此问题的有效手段。本文基于时空消耗理论，以社会福利最大化为目标函数建立多时段路网最优定价模型并给出算法，对高峰期时段实行3种不同额度的拥挤收费，得出对出行者出行时段的影响结果。通过算例分析，得出在时空资源固定的情况下拥挤收费对调节高峰时段与平峰时段的交通量分布、减少总出行交通量有显著作用，进而可以缓解城市道路的交通拥堵问题。

拥挤收费；时空资源；社会福利；交通拥堵

城市道路交通拥挤收费不同于传统意义上的道路收费，是指利用经济学中的价格原理对交通需求加以限制以缓解系统拥挤状态的交通管理手段。拥挤收费是通过对进入某一区域或某一条道路的车辆进行收费，或是对行驶在城市道路上的某一个时段的车辆进行收费，从空间和时间上来达到缓解交通拥挤的目的。新加坡是世界上最早实施城市道路收费并且获得成功的国家之一，采用ERP技术在中心商业区进行拥挤收费后，收费区域的交通量下降了10% ～ 15%，车速提高30%以上[1-2]。伦敦从2003年起在市中心22 km2的区域通过ANPR技术实行5英镑费率的通行证制收费后[3-4]，市中心交通总量降低18%(其中小汽车降低35%)，平均延误时间降低30%，车速提高了17 km/h。瑞典首都斯德哥尔摩对内城区30 km2的区域按照过渡时段、高峰时段、低峰时段分别实施拥挤收费，使得早高峰时段的出行延误时间减少了三分之一，晚高峰时段的出行延误时间减少二分之一[5]。

拥挤收费是近年来许多学者研究的热点问题， Pigou[6]首次提出拥挤收费思想，政府通过制定收费政策以增加道路使用成本，从而改变人们出行行为，进而使交通流量在时空上重新分布以达到缓解交通拥堵的目标。Liu等[7-8]利用简单路网分析拥挤收费对出行者出行路径和出行时段的影响。Gardner等[9]量化了随机拥挤收费问题的定价和出行信息的作用，并研究需求不确定和供给不确定对收费网络中网络性能和财政收入的影响。黄海军等[10]针对公共与个体两种交通方式并存的竞争系统，扩展了Tabuchi[11]的定价与方式划分研究，通过寻找出行者选择不同交通方式的成本平衡点推导和比较了各种交通收费政策下的流量分布和系统总成本，进一步加深了对竞争系统定价和方式划分问题的认识。胡怡玮等[12]基于变权层次分析法对拥堵收费状态下出行者路径选择决策问题进行分析研究，通过微调收费价格使路网中的每条路径的组合权重与该路的通行能力的比值相等，出行者按照评定的优先级向量进行路径选择。王浩庆等[13]利用广义出行费用函数，讨论拥挤收费情况下交通分配模型，并通过实例分析拥挤收费下的路段出行时间可靠度的变化情况。刘炳全[14]研究了转向限制网络基于时间的边界拥挤收费设计问题在路段和交叉口处考虑速度约束和转向限制，更加全面地体现现实交通网络的特征，提出一种新的交易旅行信用方案(或称交易旅行电子路票方案)来管理出行者的路径选择问题。

城市道路资源从时空消耗理论角度可分为时间资源和空间资源，上述研究多聚焦于拥挤收费对出行者出行路径的影响，而对出行者出行时间的研究甚少。本文从时空消耗理论角度，以拥挤收费对出行者出行时间的影响效果进行研究，并将出行者出行时段分为高峰期、平峰期1(高峰期前)、平峰期2(高峰期后)，探讨拥挤收费后，因出行成本变化引起的出行者对出行时段的选择倾向性。

1 模型假设及符号定义

1.1 模型假设

(1)本文中的交通元指小汽车和公交车；

(2)考虑小汽车和公交车两种交通方式，并假设它们之间相互独立，互不影响；

(3)出行者完全掌握路段的收费信息；

(4)只对小汽车进行拥挤收费，公交车的运行不受到拥挤收费的影响。

1.2 符号定义

L为城市道路中单条机动车道总面积，km2；T为城市道路单位服务时间(一定周期内的服务时间，如每天平均服务小时数)；Rdi为第i类别道路时空总资源，km2·h；Li为第i类别道路面积km2；η1i城市不同道路类别道路交叉口利用系数；η2i为城市不同道路类别的车道综合利用系数；lp为机动车平均出行距离，km；c为道路交通量，取路段可能通行能力，pcu/h；B为系统总效益，C为系统出行总成本，W为系统社会福利；H为所有出行时段h的集合，A为路网中所有路段a的集合；fhr,ij为连接OD对(i,j)间路径r在时段h的流量，pcu/h；I为OD对中起点i的集合，J为OD对讫点j的集合；Ph,ij为交通出行时间段h，OD对(i,j)间的出行价格；U表示不同时段下各个路段流量和OD交通量组成的可行集；xha为在出行时段h中路段a上的流量，pcu/h；cha为出行时段h中路段a上的平均成本，它是所有时段和路段交通流量的函数，cha=cha(x)；Chr,ij为连接OD对(i,j)间路径r在时段h的平均路径成本；τhr,ij为连接OD对(i,j)间路径r在时段h的拥挤定价收费；δhra,ij为开关变量，若时段h，路段a在连接OD对(i,j)的路径r上，其值为1，否则为0。

2 数学模型

2.1 模型特征

时空消耗理论是交通个体(人或车)一定时间内占用的空间或一定空间使用的时间，也可以定义为交通元在道路上占用时间与空间的乘积。根据不同类型的交通元，分为行人时空消耗、机动车时空消耗与非机动车时空消耗。

城市道路作为一时空资源，每个交通元在出行过程中既占用道路的时间资源又占用道路的空间资源。时间资源不具有重复性，当一个交通元在原来占用的位置离开后，其他交通元可以紧接占用该位置，因而道路的空间资源可以重复利用。同时，时间资源和空间资源又具有依赖性，无论是时间资源还是空间资源中任何一个被消耗完毕后，这意味着整个时空资源被消耗完毕，另一种资源失去意义。因此道路设施在一定时间和空间内所能容纳的交通需求极其有限。城市道路的时空总资源Rd是城市道路中机动车道总面积与城市道路机动车道单位服务时间的乘积[13]，即

(1)

其中，i=1,2,3,4分别表示快速路、主干路、次干路、支路。交通个体所占的城市道路时空资源Rs可表示为[15]

Rs=lp/c 。

(2)

2.2 多时段一般路网最优定价模型

从时空资源角度，城市道路由于其用地面积有限，资源总量Rd有限。从式(1)可看出，在已有道路设施下L作为城市道路中单条机动车道总面积是一个固定值，为满足日益增长的交通需求，通过拥挤收费增加城市道路服务时间内通过的总交通量，提高城市道路总资源利用率，进而可以解决城市道路的拥堵问题。

据上述假设和分析，本文建立多时段一般路网最优定价模型，在给定的收费政策下，追求系统社会福利最大化。考虑一天中H个不同时段，假定所有时段相同并等于1的多时段模型。多时段系统最优模型可表示为下列优化问题：

(3)

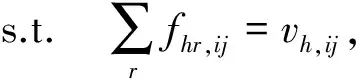
(4)

(5)

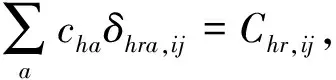
(6)

(7)

Ph,ij=Chr,ij+τhr,ij,∀h,r,i,j ，

(8)

fhr,ij,xha,cha,τha≥0 。

(9)

上式应满足以下条件：

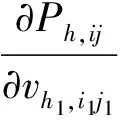
(10)

以满足，OD(i,j)在时段h的交通量对OD(i1,j1)在时段h1出行价格的影响，等于OD(i1,j1)在时段h1的交通量对OD(i,j)在时段h的出行价格的影响。出行价格Ph,ij表示OD对(i,j)在时段h的出行价格，定义为平均路径成本Chr,ij与拥挤费用τhr,ij之和。

3 算法设计

上述模型是一有约束的非线性最优化问题。模型中，假设cha是连续单调增函数，随着路段流量的增加而增加。因出行价格Ph,ij函数是需求函数的反函数，均为连续单调递减，容易证明目标函数关于xha和vh,ij是严格凸的，有唯一的系统最优路段流量和OD流量解。由传统的Frank-wolfe算法得到模型的唯一解。

令

(11)

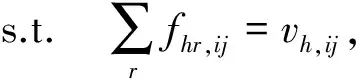
(12)

(13)

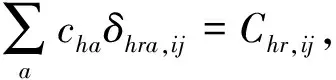
(14)

(15)

Ph,ij=Chr,ij+τhr,ij,∀h,r,i,j ，

(16)

fhr,ij,xha,cha,τha≥0 。

(17)

将式(11)简化为

(18)

s.t.Af=b,f≥0 。

(19)

设目标函数F在可行域U内可微，点x(k)∈U，目标函数F在x(k)处的线性逼近表示为

f(x)≈f(x(k))+f(x(k))T(x-x(k)) 。

(20)

用上式右边的线性函数来近似代替式(18)中的目标函数，则在x(k)的邻域有与(18)式近似的线性规划

(21)

或者等价的线性规划

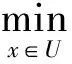
(22)

Frank-wolfe算法步骤如下：

第1步：选取初始数据。取初始可行点求x(0)∈U，给定终止误差ε>0，令K=0。

第2步：求解近似线性规划

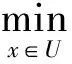
设得到最优解y(k)。

第4步：进行有效一维搜索。求解线搜索问题

minf(x(k)+λd(k))，s.t. 0≤λ≤1 。

设得最优解λk。令x(k+1)=x(k)+λkp(k)，k=k+1，转第二步。

4 算例分析

在拥挤收费作用下，假设出行者只改变自己的出行时间而不改变出行路径。将出行者出行时间分为3个长度相等的时段，令式(11)中h=1,2,3。其中，当h=2，表示处于交通高峰期；当h=1,3时分别表示交通处于平峰期1(高峰期前)和平峰期2(高峰期后)。a=A=1，表示只选取一条路段进行分析。因此式(11)可简化为：

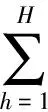
(23)

路段不收费时广义费用函数为：

(24)

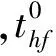
(25)

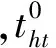
表1 收取拥挤费τ1=1元出行者的出行时间分布对比

由表1得出，在实施拥挤收费τ1=1元前，出行者的出行时间分布呈现“驼峰”现象，在h=2(高峰期)出行者分布较为集中，在h=1或h=3(平峰期)出行者分布较为松散。实施拥挤收费以后，首先出行总量较之收费前下降1.97%。由于在高峰期出行成本的增加，部分出行者会改变自己出行时间，提前或者延后自己的出行。这使得出行者的出行时间分布与收费之前相比，呈现一个“削峰填谷”分布。在h=1时，收费后的出行量增加9.63%；在h=2时，收费后的出行量下降11.92%；在h=3时，收费后的出行量增加12.19%。

表2 收取拥挤费 τ2=2元出行者的出行时间分布对比

表2为收取拥挤费τ2=2元后出行者的出行时间分布对比。在增加收费额度之后，出行总量下降3.29%，下降幅度明显增加。在h=1时，收费后的出行量增加17.28%；在h=2时，收费后的出行量下降18.08%；在h=3时，收费后的出行量增加13.96%。在实行τ2=2元的收费后高峰期的出行量下降明显且要比τ1=1元下降幅度明显，说明适当增加拥挤收费额度可以提高缓解交通拥堵的效果。

表3 收取拥挤费 τ3=4元出行者的出行时间分布对比

表3较之表2中的拥挤收费，增加一定额度。增加收费额度后出行总量下降4.68%，下降幅度又有新的提升。在h=1时，收费后的出行量增加34.13%；在h=2时，收费后的出行量下降30.18%；在h=3时，收费后的出行量增加21.18%。从上述数据看出，在收费额度从τ2=2元增加到τ3=4元后，高峰期出行量下降幅度很大，在h=1时段内出行者数量变化明显，远大于h=3时段内的出行量。这说明增加收费额度到一定值后，出行者为了降低其出行成本，更倾向于提前自己的出行时间。

图2 拥挤收费前后出行者出行密度等高线图
Fig.2 The contour plot of travel density before and after congestion charging

图2a给出了拥挤收费前出行者的出行密度等高线，在实施收费前出行者出行密度跨度较大，出行者出行时间选择较为密集。图2b为拥挤收费后出行者出行密度等高线，与图2a相比，在实施收费后，因出行成本的增加，部分出行者避开高峰拥挤时段，向平峰时段转移。这使得出行者出行密度跨度较小，出行时间分布较为均匀。

5 结论

本文研究了拥挤收费下出行者对出行时间的选择，建立了相应的模型，给出了相应的算法及求解，得出出行者为降低出行成本，在拥挤收费下会改变原来的出行时间甚至取消出行计划。对比分析3个不同费用额度的拥挤收费，得出了出行者在不得已改变其出行时间时，相比延后出行时间而更倾向于提前自己的出行时间。当收费额度达到较高值时，出行者出行总量下降幅度明显增大，说明对高峰期实施适当的收费政策可以有效缓解城市道路的拥堵问题。最后得出拥挤收费前后出行者出行密度等高图，发现收费后出行者集聚在高峰时段出行这一现象明显减轻，从侧面反映出拥挤收费可以缓解交通拥堵问题。

[1]GOH M. Congestion management and electronic road pricing in Singapore [J]. Journal of Transport Geography, 2002, 10(1):29-38.

[2]PHANG S P, TOH R S. From manual to electronic road congestion pricing: The Singapore experience and experiment [J]. Transportation Research Part E: Logistics and Transportation Review, 1997, 33(2):97-106.

[3]KIM K S, HWANG K. An application of road pricing schemes to urban expresswaysin Seoul [J]. Cities, 2005, 22(1):43-53.

[4]PRUD'HOMME R, BOCAREJO J P. The London congestion charge: a tentative economic appraisal[J]. Transport Policy, 2005, 12(3): 279-287.

[5]ELIASSON J, HULTKRANTZ L, NERHAGEN L, et al. The Stockholm congestion-charging trial 2006: Overview of effects[J]. Transportation Research Part A: Policy and Practice, 2009, 43(3): 240-250.

[6]PIGOU A C. The Economics of Welfare [M].London: MacMillan, 1920:70-73.

[7]LIU L N, MCDONALD J F. Efficient congestion tolls in the presence of unpriced congestion: a peak and off-peak simulation model[J]. Journal of Urban Economics, 1998, 44(3): 352-366.

[8]LIU L N, MCDONALD J F. Economic efficiency of second-best congestion pricing schemes in urban highway systems[J]. Transportation Research Part B: Methodological, 1999, 33(3): 157-188.

[9]GARDNER L M, BOYLES S D, WALLER S T. Quantifying the benefit of responsive pricing and travel information in the stochastic congestion pricing problem[J]. Transportation Research Part A: Policy and Practice, 2011, 45(3): 204-218.

[10]黄海军,BELL M G H,杨海.公共与个体竞争交通系统的定价研究[J].管理科学学报, 1998 , 1(2):17-23.

[11]TABUCHI T. Bottleneck congestion and modal split[J]. Journal of Urban Economics, 1993, 34(3): 414-431.

[12]胡怡玮，李正刚，胡万欣，等. 基于变权层次分析法的拥挤收费路径选择研究[J].重庆交通大学学报(自然科学版)，2014,33(6):127-131.

[13]王浩庆.基于出行时间可靠度的拥挤收费研究[D].成都:西南交通大学，2015:5-6.

[14]刘炳全.城市交通网络拥挤收费设计：模型与算法[D].武汉: 武汉大学，2014:4-5.

[15]郑安文，朱晓宏，邵正宇，等. 城市道路交通供给能力研究[J].应用基础与工程科学学报, 2002, 10(4): 429-435.

Analysis of the influence on travelers’ choice of travel time under the congestion pricing

YUE Xian-fei1,2, FU Bai-bai2,3*,WU Ke-xin1

(1. School of Transportation Engineering, Shandong Jianzhu University, Jinan 250101, China；2. Traffic Research Institute of Shandong Jianzhu University，Jinan 250101, China；3.School of Architecture and Urban Planning, Shandong Jianzhu University, Jinan 250101, China)

∶With the sustainable growth of urban vehicles’ ownership, it makes the road congestion become an increasingly serious problem. And it is an effective means to solve the urban road congestion by increasing the utilization rate of current road resources through congestion charging. Based on the theory of time-space consumption, the optimal pricing model of multi-time road network was established to achieve the maximum social welfare as the destination function and the corresponding algorithm was given in this paper. To the peak period, three different amounts of congestion charges were applied to get the influence on travelers’ travel time. Finally, the algorithm case was analyzed to prove that when the time-space resources are fixed, congestion pricing has a significant effect on regulating the traffic volume distribution during normal periods and peak periods, and reducing the total traffic volume, thus relieving the traffic congestion in urban roads.

∶congestion pricing; time-space resource; social welfare; traffic congestion

10.3976/j.issn.1002-4026.2017.03.011

2016-10-22

国家自然科学基金(71171124，71471104，71371026)

岳贤飞(1990—)，男，硕士研究生，研究方向为交通运输规划。

*通信作者，傅白白。E-mail：fubaibai@163.com

U491

A

1002-4026(2017)03-0058-07