海洋水文气象观测设备误差校准算法研究

杨俊贤，万婧，刘忠民，赵杰，杨立，朱洪海，惠力，杨英

(1.山东省科学院海洋仪器仪表研究所，山东省海洋环境监测技术重点实验室，山东 青岛 266001；2.山东省海洋仪器仪表科技中心，山东 青岛 266001 3.国家海洋局烟台海洋环境监测中心站，山东 烟台 264011)



【海洋科技与装备】

海洋水文气象观测设备误差校准算法研究

杨俊贤1，万婧2，刘忠民3，赵杰1，杨立1，朱洪海1，惠力1，杨英1

(1.山东省科学院海洋仪器仪表研究所，山东省海洋环境监测技术重点实验室，山东 青岛 266001；2.山东省海洋仪器仪表科技中心，山东 青岛 266001 3.国家海洋局烟台海洋环境监测中心站，山东 烟台 264011)

为了提高海洋水文气象数据采集精度，需要对观测设备获得的数据参数进行误差校准标定。本文分别对分段线性化算法、最小二乘法的曲线拟合计算方法和样条函数分段三次多项式算法进行对比分析，最终将通过所有误差标定点且标定点处曲线光滑连续的样条函数分段三次多项式曲线拟合法，作为标准数据与观测数据进行误差校准标定的基本方法。通过实验对比分析，三次样条函数分段拟合误差标定法能够降低数据测量误差，保证观测设备获得较为准确、可靠的数据参数。

水文气象观测;最小二乘法;样条函数分段拟合;误差校准

海洋环境监测对国家海洋经济发展、环境保护、防灾减灾、国防安全具有至关重要的作用，因此，世界各国都非常重视海洋环境的观测工作[1]。岸边海洋台站采用水文气象观测设备对海洋参数单要素或多要素进行全天候自动化观测，以保证海洋水文气象观测数据的连续性和可靠性。水文气象观测设备集成很多要素的传感器，如风、温湿、雨量、气压、温盐等等，在长期连续的使用过程中传感器输出的数据会产生偏差[2]。为了降低误差，保证观测数据的准确性，根据标准计量部门每次给出的数据误差报告，通过分段线性化、最小二乘法和样条函数分段三次多项式3种方法进行了计算对比分析，最终选择三次样条函数误差校准算法对观测数据进行现场快速有效标定。

1 误差标定算法

观测设备的误差校正，首先通过高精度测试方法将误差从设备中分离出来，得到一组离散的误差值。分离出的离散误差值作为采样点的实际误差值，进行数据拟合，得到一个连续的误差曲线。根据拟合的误差曲线进行插值计算，实现在测量范围内对任意点数据进行误差校正。为了最大限度地接近实际的误差曲线，拟合曲线应尽可能的通过所有的实际误差点，降低标准数据的损失[3]。另外，在保证拟合精度的前提下，还需要采用简单、方便、运算快、易于实际应用的拟合曲线。

1.1 分段线性化标定

分段线性化的基本原理就是把一定量程范围内的输入与输出呈非线性关系的数据分成若干段，在每一段上可以认为输入与输出之间存在着线性关系，即输入的局部范围内，其输入和输出可以近似地认为是线性关系[4]。理论上，只要分段数量足够多，任何连续的函数都可以用分段线性化来处理分析。

设输入为x，分成若干段为x1,x2,x3，…，xn，输出y分别对应为y1,y2,y3，…，yn，如图1所示。

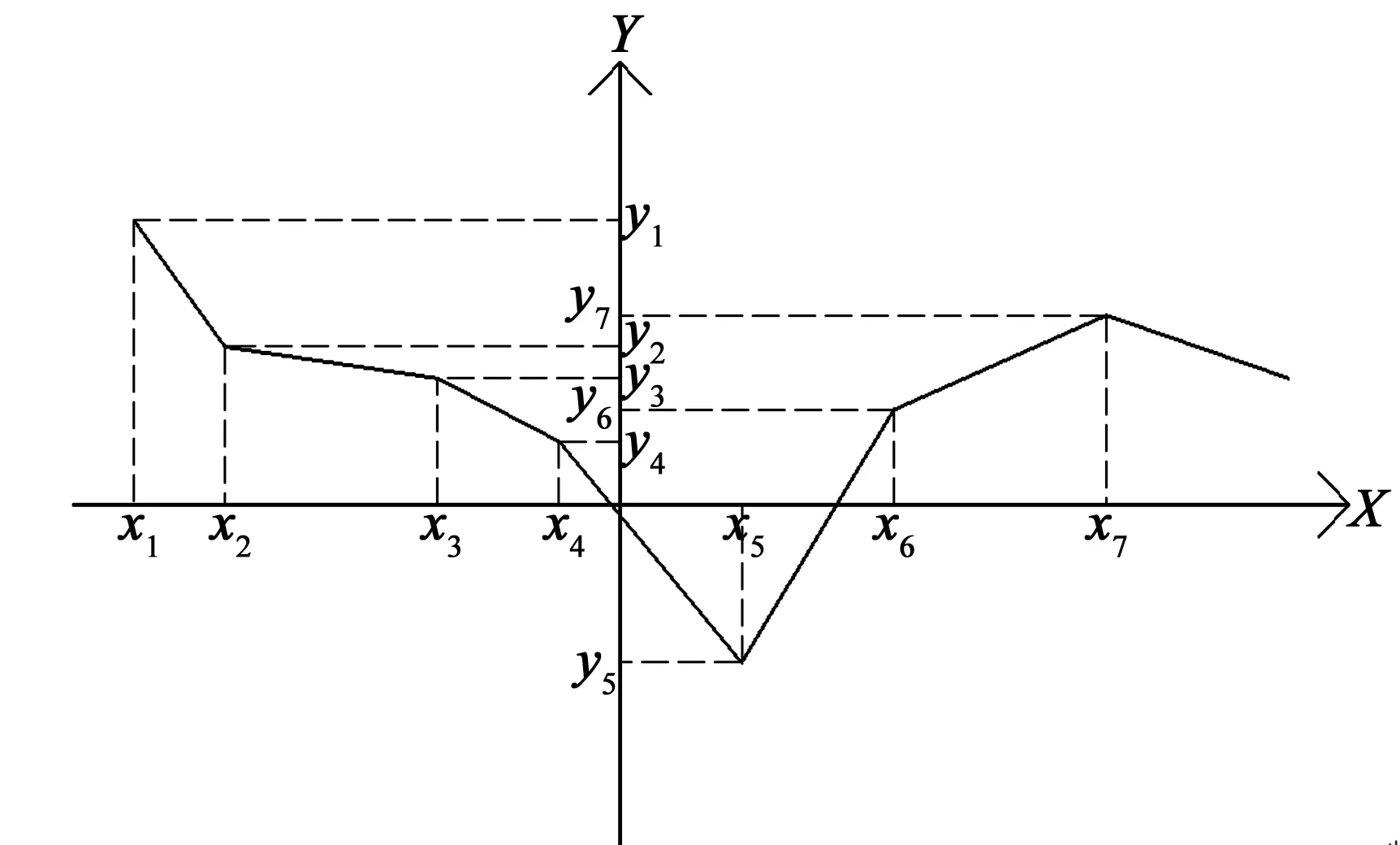
图1 分段线性化分段示意图Fig.1 Piecewise linear block diagram

图中表明共有7组数据，共分成6段，每一段数据要根据数据点进行斜率计算，计算公式如式(1)所示：

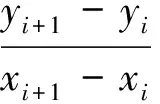
(1)

对于分段范围内的数据，要严格按照分段运算公式进行计算，不能超出分段限定，否则会增大数据误差范围。输入与输出的分段计算公式为：

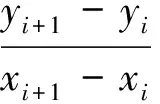
(2)

分段线性化方法能够保证通过所有标准误差点，但是在每个分离误差标准点处斜率不连续，其左右斜率有一个数据跳跃变，曲线不光滑，整体误差曲线拟合精度较低[5]。但分段线性化具有其函数曲线模型简单、计算方便、软件程序编写方便等特点，在没有上位机软件协助处理的情况下，此方法应用较广。

1.2 最小二乘法多项式拟合

最小二乘法多项式拟合误差曲线就是从标准误差数据集(xi,yi)(i=0, 1, 2，…，n)中求整体误差函数P(x)的数值方法。该方法可实现离散误差数据点(xi,yi)(i=0, 1, 2,…,n)，只用一个多项式函数P(x)来表示整体误差的变换趋势[6]。拟合的处理就是误差λi=P(xi)-yi(i=0, 1, 2,…,n)，按最小二乘法原则使其残差的平方和最小，即式(3)所示。

(3)

在离散数据的最小二乘拟合中，最常用的数学多项式模型如式(4)所示，正则方程如式(5)所示。参数校正采用3次曲线拟合的方法，将标定数据分为8段进行三次曲线拟合，其误差范围较小[7]。

(4)

(5)

以温度的校准为例，已知温度的8组测量值与实际值得的比对报告如表1所示。

表1 温度测量值与实际值比对

参照公式(5)将测量值与实际值代入正则方程组求解三次曲线拟合多项式系数a0，a1，a2，a3。拟合多项式计算得到的系数为a0=-0.432 37，a1=1.113 44，a2=-0.007 81，a3=0.000 132 463 8，多项式拟合曲线如图2所示。

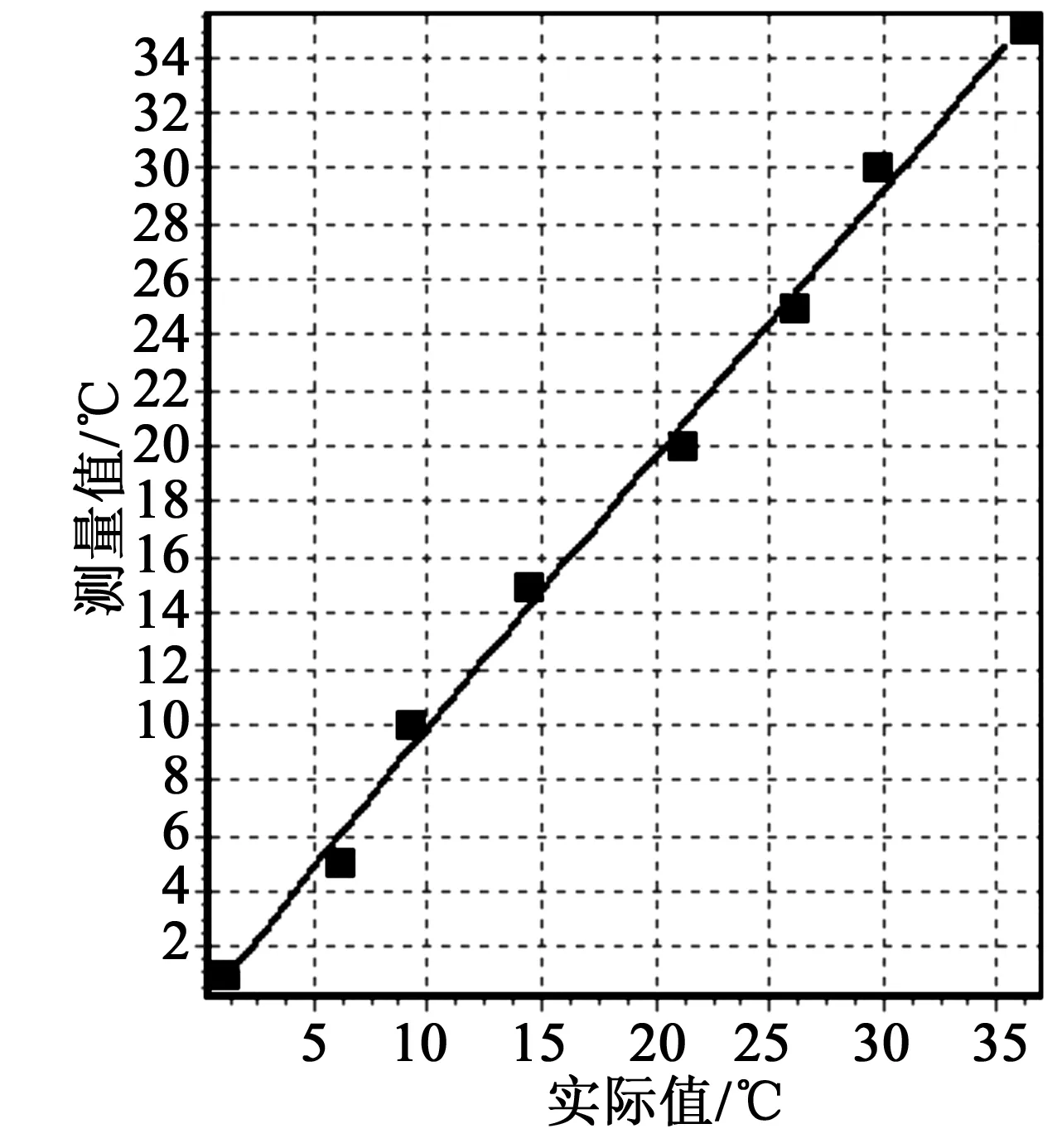
图2 多项式拟合曲线图Fig.2 Polynomial fitting curve

虽然最小二乘多项式拟合法数据模型具有简单、运算方便、计算快等特点，但是在实际误差校准应用中存在不确定性[8]。从图2可以看出，最小二乘法拟合曲线不能完全通过所有标准误差点，多数只是接近标定值，因此标准误差点损失较大，误差的校准精度很难保证。

最小二乘法的函数曲线模型具有一定的主观性，只有在分离后的误差数据序列有明显规律的情况下，拟合曲线才能在实际中应用。与最小二乘法不同，样条函数拟合的方法，可以拟合标定分离出具有各种变化趋势的标准误差点，确保函数曲线经过所有离散标定误差点。

1.3 样条函数分段三次多项式

样条函数三次多项式误差标定算法属于一种分段函数标定，它在分离标准误差点构成的每个小区间上是三次多项式[9]。拟合曲线能够通过每个标准误差点，并且具有连续的一阶、二阶导数，保证标定点斜率连续性。

设si(x)为两个相邻标准误差点(xi,yi)，(xi+1,yi+1)之间的分段三次多项式函数，公式为：

si(m)=ai+bim+cim2+dim3

(6)

上式中m代表节点x轴的区间宽度，i=1，2，…，n。根据标准误差点和已知条件，求出样条曲线方程中的4n个未知系数ai，bi，ci，di，得到每段曲线函数表达式，根据表达式可对分段区间内的数据进行误差标定。求解条件公式如(7)所示。

(7)

其中，si(mi)中mi=xi-xi=0,i=1,2,…，n。si(mi+1)中mi+1=xi+1-xi，i=1,2，…，n-1。

求解公式(7)只能满足4n-2个方程，需要根据自然边界条件补足两个定解方程式，就可求得分段三次多项式函数未知系数。

(8)

设λi=s″i(xi)=2ci，代入式(8)中，可得到λi与mi，yi的关系式(8)，将数据节点和指定的首位端点条件带入矩阵方程，求解三对角矩阵，获得二次微分值λi，从而获得未知系数值。

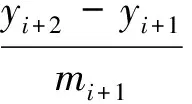
(9)

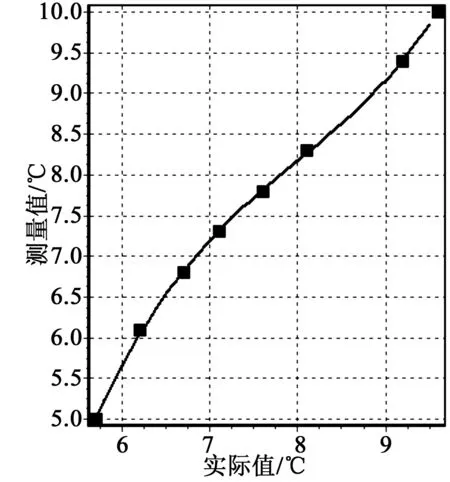
图3 分段三次多项式拟合曲线图Fig.3Piecewise cubic polynomial fitting curve

以表1中的数据为例，取标定参数点(5.7，5.0)和(9.6，10.0)，求得的系数为a2=-46.670，b2=18.833，c2=-2.248，d2=0.094，曲线如图3所示。

误差标定曲线采用样条函数分段三次多项式拟合的方法，保证拟合曲线二阶连续而且光滑，误差曲线拟合效果好，校准误差准确率高[11]。由于样条函数三次多项式系数的确定需要求解一个线性方程组，计算量增大，因此为了减少运算量，三次样条函数的构造采用追赶法求解一个三对角型方程组。根据数据计算的复杂程度，数据拟合与插值计算仍然须借助上位机软件对水文气象观测设备进行误差修正。

2 实验结果

以温度测量为例，取表1中标定参数点(5.7，5.0)和(9.6，10.0)数据段之间的数值进行3种误差标定算法的对比分析，如表2所示。

表2 3种误差标定算法对比表

将两组标定点数值代入公式(1)得k=1.282，将表2中的测量值代入公式(2)可以得到分段线性化误差标定后的数据，图4中将标准值，测量值和分段线性化标定后的值进行对比分析，可见分段线性化标定后的数据趋势基本接近标准值，但是在对测量值6.4～7.8 ℃的范围内的标定值与标准值之间有一定的偏差。

参照表1中的测量值与实际值的8组标定点，代入公式(5)得到最小二乘法三次多项式系数a0=-0.432 37，a1=1.113 44，a2=-0.007 81，a3=0.000 13，将该系数和表2中测量值代入公式(4)，得到最小二乘法误差标定后数据，图5中应用最小二乘法标定后的数值与测量值之间的数据变化不大，实际中最小二乘法在标定参数点(5.7，5.0)和(9.6，10.0)数据段之间没有达到误差标定目的。

参照表1中的测量值与实际值的8组标定点，代入公式(8)得到样条函数分段三次多项式系数a2=-46.670，b2=18.833，c2=-2.248，d2=0.094 ，将该系数和表2中测量值代入公式(4)，得到样条函数分段三次多项式误差标定后数据，通过图6可以明显看出采用样条函数三次多项式进行误差标定后的数据与标准值之间的数据基本重合，因此在实际应用中采用样条函数法来进行数据误差校准能够达到很好的效果。

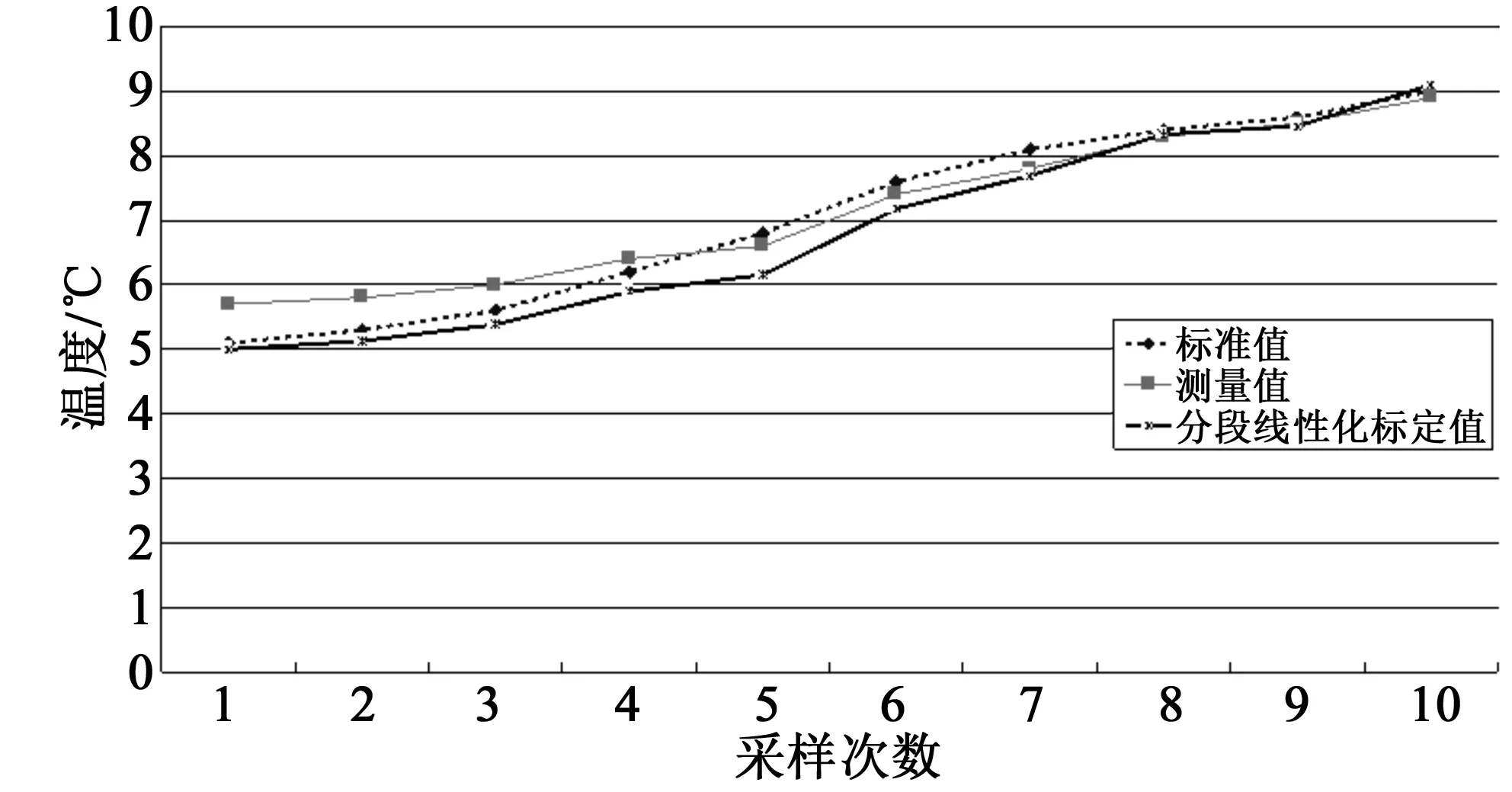
图4 分段线性化标定分析对比图 Fig.4 Contrast figure of piecewise linearization calibration analysis

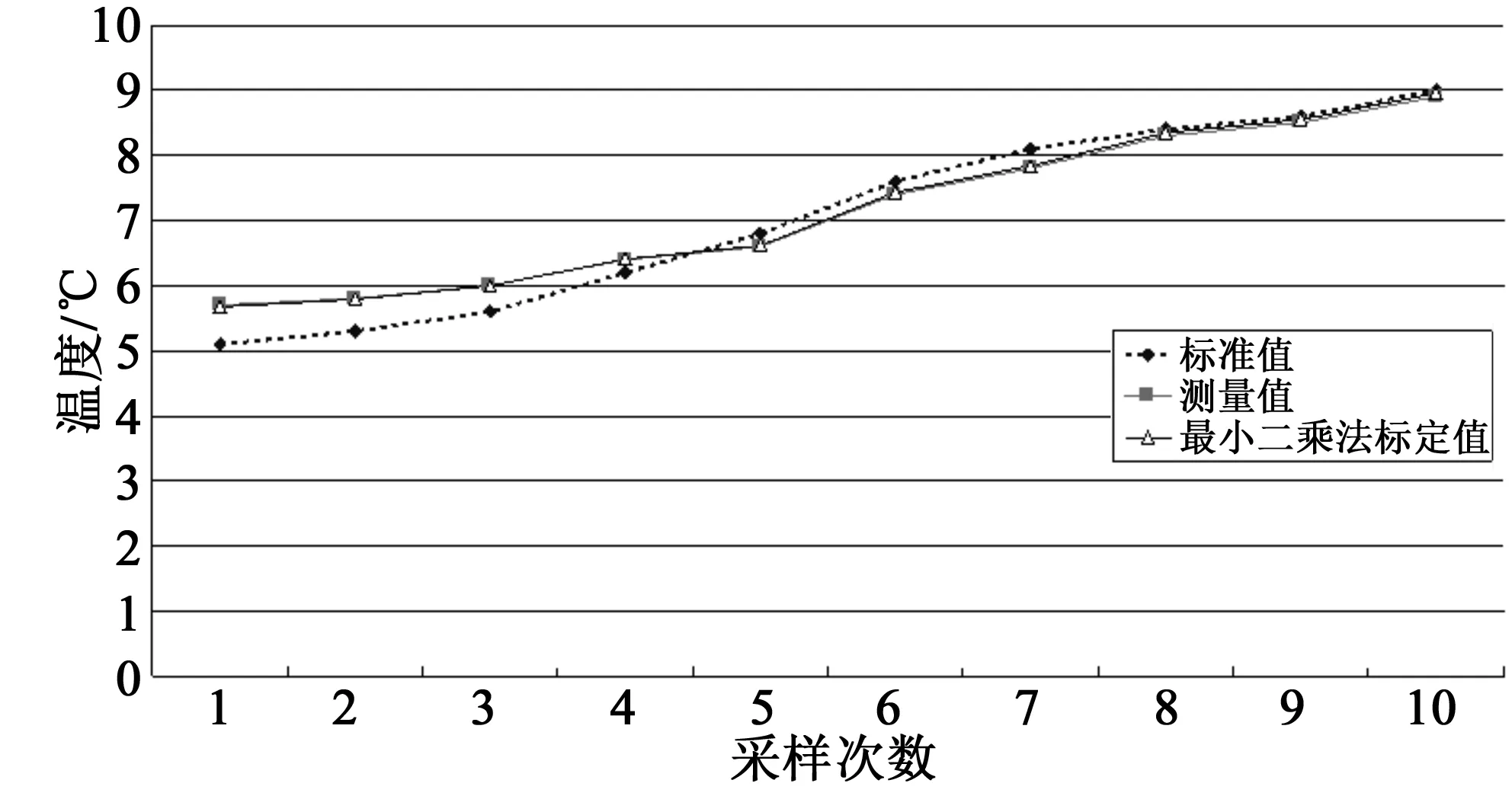
图5 最小二乘法标定分析对比图Fig.5 Contrast figure of least squares calibration analysis

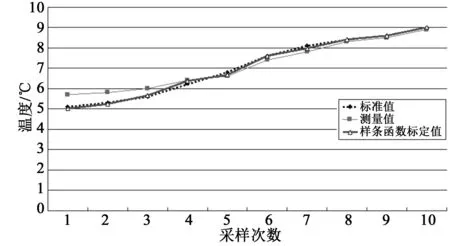
图6 样条函数标定分析对比图Fig.6 Contrast figure of spline function calibration analysis

3 应用实例

水文气象观测设备每3 s采集一次温度数据，将计算得到约平均每分钟温度值传到上位机。通过上位机软件对温度误差数据进行三次样条函数校正处理[10]。截取24 h内一段时间的气温连续观测数据进行校正前后对比分析，如图7和图8所示。

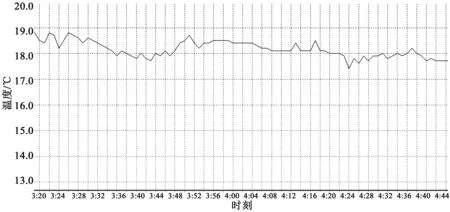
图7 三次样条函数校正前温度连续观测曲线Fig.7 The temperature curve of continuous observation before cubic spline function correction

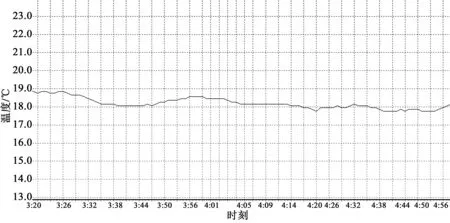
图8 三次样条函数校正后温度连续观测曲线Fig.8 The temperature curve of continuous observation after cubic spline function correction

通过图7和图8的曲线对比可以看出，未采用三次样条函数误差校正的平均温度观测值存在一定的误差，每分钟温度值跳动较为明显。采用三次样条函数误差校正算法进行标定后，测量误差降低，每分钟之间温度变化相对较小，整体曲线变化较为平滑，得到较准确的温度值。

4 结论

水文气象是海洋重要的观测要素，数据的准确性直接影响到海洋预报、渔业生产、港口作业等各项工作[12]。本文通过分段线性化标定算法、最小二乘法的多项式曲线拟合的标定方法和样条函数分段三次多项式标定方法进行优缺点对比分析，最终采用样条函数分段三次多项式的方法来实现误差校准标定。分析结果表明，分段线性化能够通过所有的标定点，但在误差标定点处斜率跳动较大，容易引起标定点附近的数据标定误差；最小二乘法虽然曲线光滑，但标定点的数据损失较大；样条函数分段三次多项式曲线拟合法能够通过所有误差标定点且标定点处拟合曲线光滑连续，因此样条函数法在校准标定上是有一定的应用和推广价值的。

[1]封秀燕，何志军，王荷平，等.自动气象站实时资料质量控制开放式平台设计[J].应用气象学报,2010,21(4):506-512.

[2]魏文健.自动气象站数据采集器的计量检测和结果处理方法[J].气象水文海洋仪器,2005(3/4):52-55.

[3]费业泰.误差理论与数据处理[M].北京:机械工业出版社，1981.

[4]叶凌箭，钟伟红，宋执环. 基于分段线性化法的改进自主优化控制[J].自动化学报,2013,39(8),1231-1237.

[5]吕游，刘吉臻，赵文杰，等. 基于分段曲线拟合的稳态检测方法[J].仪器仪表学报，2012,33(1),194-200.

[6]都强，杭柏林. 最小二乘法在多传感器测量标定中的应用[J].传感器技术学报,2005,18(2),244-246.

[7]高伟，姜水生. 分段曲线拟合与离散度加权的数据误差处理方法[J].中国测试技术,2005,31(6),55-56.

[8]伊杭，张伟等. 一种MEMS加速度计误差分析与校准方法[J].传感器技术学报,2014,27(7):866-869.

[9]海啸，朱志杰. 最小二乘法和三次样条曲线拟合的比色测温误差修正对比分析[J].激光杂志,2015,36(6)：72-76.

[10]陈浩，华灯鑫，张毅坤，等. 基于三次样条函数的激光雷达数据可视化插值法[J].仪器仪表学报,2013,34(4):831-837.

[11]张旭臣，卢全海. 基于分段二次样条函数的水位流量关系曲线拟合方法研究[J].水文,2010,30(4):59-62.

[12]李志鹏，张玮，黄少平，等.自动气象站数据实时质量控制业务软件设计与实现[J].气象,2012,38(3):371-376.

Research on the error calibration algorithm of the marine hydro-meteorological observation equipment

YANG Jun-xian1，WAN Jing2，LIU Zhong-min3，ZHAO Jie1，YANG Li1，ZHU Hong-hai1，HUI Li1，YANG Ying1

(1.Institute of Oceanographic Instrumentation Shandong Academy of Sciences ，Shandong Provincial Key Laboratory of Ocean Environment Monitoring Technology，Qingdao 266001,China；2.Shandong Oceanographic Instrumentation Science Center, Qingdao 266001, China；3.Yantai Marine Environment Monitoring Center Station，SOA,Yantai 264011，China)

∶ In order to improve the precision of hydro-meteorological observation data acquisition, the error calibration was needed for the data parameters obtained from the observation equipment. In this paper, three kinds of error calibration algorithm including piecewise linearization, least squares curve fitting and three polynomial of spline function were compared. Finally, three polynomial fitting of spline function method, which could pass through all the error calibration points and have smooth and continuous curve near the calibration points, was determined to be used for error calibration of the observation data. The experimental comparative analysis shows that three spline function fitting error calibration method can reduce the data measurement error and ensure the observation equipment to obtain a more accurate and reliable data parameter.

∶hydro-meteorological observation; least square method; spline function fitting; error calibration

10.3976/j.issn.1002-4026.2017.03.001

2017-01-13

国家重点研发计划(2016YFC1400403)

杨俊贤(1981—)，女，硕士，工程师，研究方向为海洋装备技术。E-mail：yjxwork@126.com

P715

A

1002-4026(2017)03-0001-07