新意法在野猪山隧道施工中的应用研究

王克忠，朱海斌，孔令民，梁其东，张海军

(1.浙江工业大学 建筑工程学院，浙江 杭州 310014；2.日照市供水管理处，山东 日照 276800)

新意法在野猪山隧道施工中的应用研究

王克忠1，朱海斌1，孔令民2，梁其东2，张海军1

(1.浙江工业大学 建筑工程学院，浙江 杭州 310014；2.日照市供水管理处，山东 日照 276800)

为探讨新意法在复杂地质环境下隧道施工中的可行性，依托具体工程，对山岭隧洞出口段进行了数值仿真分析，研究了新意法和台阶法开挖时掌子面的纵向内空变形和应力变化规律，预测了沿隧道轴线方向拱顶沉降的时空变化规律，对比分析了隧道不同开挖、临时加固方式对掌子面大变形、失稳的影响，得出了掌子面中部易失稳，新意法施工可有效抑制掌子面变形的结论，对同类隧道工程研究具有一定的理论意义，并对工程实践具有重要参考价值.

新意法；台阶法；掌子面；数值模拟

山岭隧道出口段围岩破碎，在隧道开挖后，掌子面应力解除，围岩应力重分布[1]，隧道出口段坍塌、冒顶和掌子面失稳等现象时常发生.多年来，国内外一些专家、学者采用解析法、模型试验法和经验公式法等[2]对隧道出口段开展了大量研究.周艺等[3]以现场试验结果为依据，结合数值仿真模拟，对比分析了隧道在不同开挖方法下的围岩变形特征、初期支护和二衬的内力变化规律.赵录学[4]依据新意法原理，对特殊工程环境下隧道选线、支护参数的优化和施工方案进行了探讨，为新意法在我国的推广应用提供了借鉴.国内外参考文献表明，国内学者利用新意法的理论，对超前预加固在软岩浅埋隧道施工的作用进行了研究[5-7]，但未能全面阐释施工中围岩力学与变形规律.笔者依托野猪山隧道工程，采用有限元软件Midas/GTS对新意法和台阶法的施工过程进行了数值仿真计算，并结合监测数据对比分析了两种施工方法在浅埋软弱地层中的适用性，为今后同类工程的设计和施工提供了借鉴.

1 掌子面失稳判据

岩石强度理论是与隧道掌子面的失稳机理紧密相关的，反映了岩石破坏时的应力状态或变形状态.目前广泛应用的强度理论，多数是从应力观点来考察材料破坏的，其中库伦-莫尔强度理论就是应力观点强度理论的继续和发展.

库伦在1773年提出了，当材料某截面上的剪应力达到黏聚力与内摩擦力之和时，材料将发生剪切破坏.土体剪切破坏准则的库伦准则表达式[8]为

τn=c-σntanφ

(1)

式中：τn为极限抗剪强度；σn为剪切面上的法向应力；c，φ分别为土的黏聚力和内摩擦角.

摩尔(1882)将库伦破坏条件表示为与最大主应力圆相切的一条直线，当σ1≥σ2≥σ3时，由图1可推导各主应力关系式为

(2)

屈服面方程为

(3)

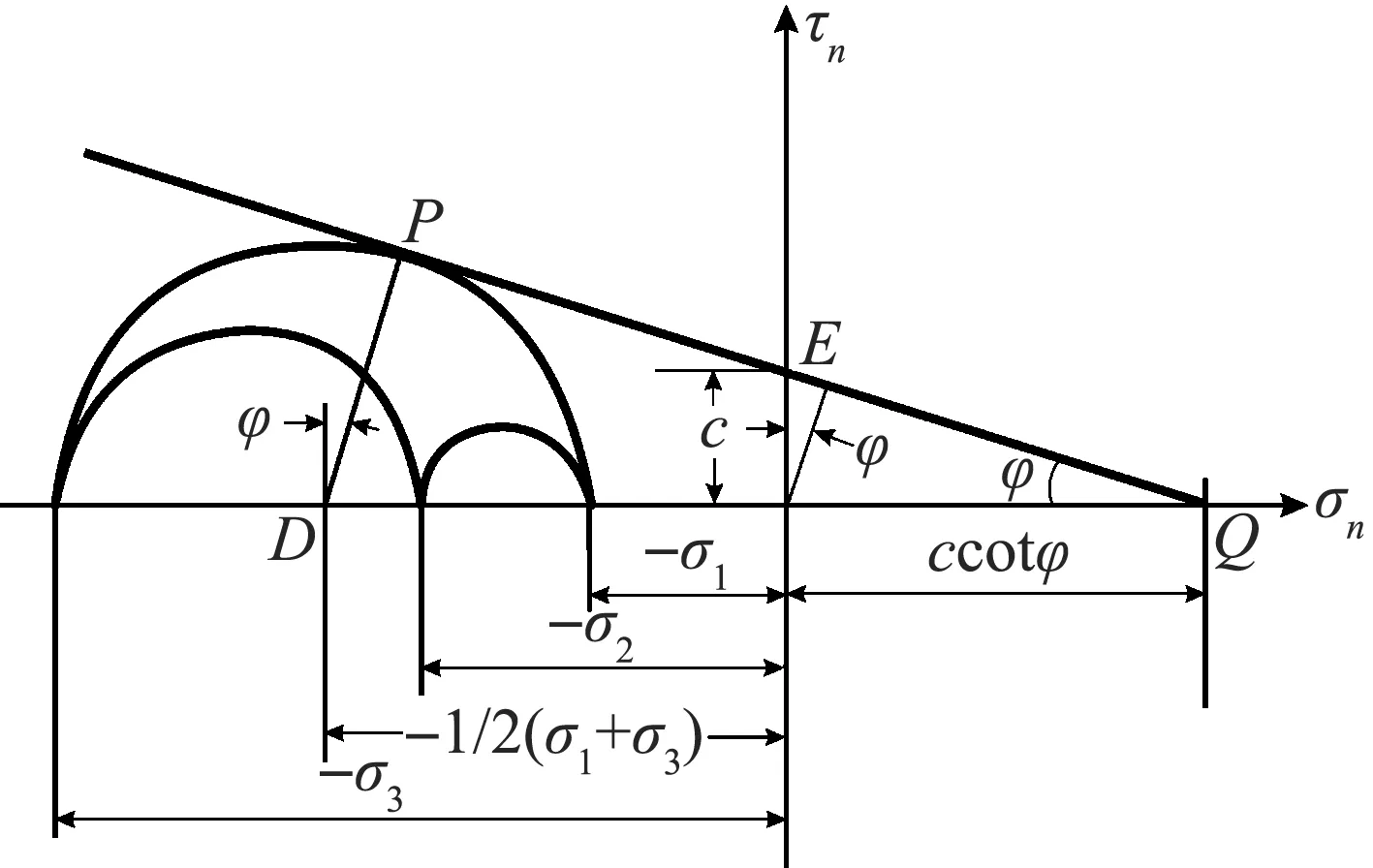
图1 摩尔-库仑破坏条件Fig.1 Mohr-Coulomb failure conditions

如何判别掌子面是否处于整体失稳状态是隧道有限元稳定分析的一个关键问题.按照岩土力学中的摩尔-库伦屈服准则，隧道掌子面失稳时破坏面上各点应力都达到极限平衡状态，极限应力圆与屈服面相切.因此，有限元分析时以掌子面在开挖过程中应力状态与屈服面的关系作为失稳判据是比较合理的.

2 数值仿真模拟

2.1 工程简介

野猪山隧道为分离式隧道，两隧洞相距约35m.其出口段分布残坡积、洪积含碎石粉质黏土和含黏性土碎石，褐黄色，碎石较多为强风化岩块，厚度较大，埋深为10～20m.两隧洞出口段分别采用新意法和台阶法两种施工方法，两种工法初期支护一致，采用25cm厚C25喷射混凝土、锚杆、钢筋网与钢架联合支护，钢拱架为18号工字钢，纵向间距为0.5m.

2.2 模型及边界条件

采用Midas/GTS建立三维有限元模型，由于野猪山两隧洞相距较远，相互影响可忽略不计，故对单洞施工过程进行模拟.选取野猪山隧道出口段50m进行数值仿真分析.以模型正面隧道底部中心为原点，取隧道轴线在水平面上的投影线为y轴，其正方向由洞口指向隧洞内部，x轴垂直隧洞轴线，z轴的正方向为竖直向上.模型范围：-40 m≤x≤40 m，0≤y≤50 m，-35 m≤z≤地面.该模型上边界设为自由边界.以隧道开挖跨度的3～5倍[9]选取模型左右边界和底部边界，其中模型底部边界设置竖向约束，其余各边界分别设置该方向上的水平约束，计算模型如图2所示.

图2 计算模型Fig.2 Calculation model

2.3 模型参数选定

计算本构模型采用Mohr-coulomb屈服准则，选取弹塑性模型进行计算.采用板单元模拟喷射混凝土，用植入桁架单元模拟锚杆，钢拱架采用等效计算的方法[10]并参考型钢型号将弹性模量折算并附加到混凝土喷层中，其中折算喷混层的纵向长度为0.5 m，计算式为

E=E0+Sg·Eg/Sc

(4)

式中：E为折算后等效初期支护的弹性模量；E0为原混凝土材料的弹性模量；Sg为钢拱架的截面积；Sc为混凝土截面积；Eg为钢材的弹性模量.

参照野猪山隧道工程地质勘察报告中的地层物理参数，土体划分为3层.具体物理力学参数如表1，2所示.

表1 岩体计算参数

表2 支护计算参数

2.4 施工模拟

为比较台阶法和新意法施工的优缺点及其对掌子面稳定性的影响，对两种工法下隧道的开挖及支护过程进行了对比分析研究.台阶法施工：采用三台阶法开挖，先后开挖第一步和第二步台阶，各开挖8 m和4 m并支护，再以1 m为一个循环进尺，每一个循环完成后及时施做初期支护，施工工序如图3所示.

新意法施工:采用全断面开挖，以1 m为一个循环进尺，开挖前掌子面植入玻璃纤维锚杆并注浆进行超前预加固，保证锚杆嵌入掌子面前方至少12 m，搭接6 m，掌子面锚杆布置间距为120 mm，如图4所示.

图3 台阶法开挖工序Fig.3 Process of bench cut method

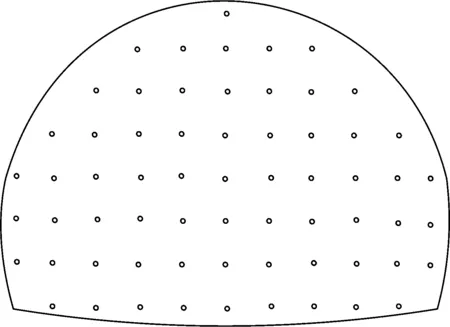
图4 新意法掌子面锚杆布置Fig.4 Arrangement of anchors on excavated face of ADECO-RS approach

3 计算结果及分析

3.1 掌子面挤出位移

岩土控制变形分析法依据超前核心围岩体系的应力—应变状态，把掌子面稳定形态分为3类[11-12]：稳定状态、短期稳定状态和不稳定状态.而掌子面超前核心岩土体稳定性将直接影响到掌子面的挤出位移.掌子面挤出位移超过某个界限就表明掌子面稳定状态转变为短期稳定或不稳定状态.

三台阶法开挖时，上、中、下三个台阶的掌子面沿隧道纵向产生不同程度的挤出位移，土体出现鼓出现象，其中最大位移出现在下台阶，达到15 mm左右，如图5所示(单位为m).

新意法施工时，掌子面同样出现挤出位移，最大位移出现在掌子面中心附近，达到8 mm左右，相比于台阶法开挖缩小了近一半，如图6所示(单位为m).新意法施工改变了开挖面处超前核心土的强度和刚度，一定程度上抑制了掌子面过大变形.

图5 台阶法掌子面纵向位移图Fig.5 Longitudinal displacement on excavated face of bench cut method

图6 新意法掌子面纵向位移图Fig.6 Longitudinal displacement on excavated face of ADECO-RS approach

3.2 掌子面应力状态

根据掌子面的挤出位移可知：在施工过程中掌子面稳定性最差的部位在掌子面中心附近.下面选取台阶法上、中、下三个台阶各开挖到30 m处时，与三个台阶相对应的掌子面中心附近的节点作为研究对象，同时新意法三个测点的位置与台阶法的三个节点相对应，然后通过偏应力和球应力的关系曲线，分析以上节点在开挖过程中的屈服轨迹和应力变化趋势.其中，围岩采用摩尔-库伦准则[13]，以其Mohr形式作为屈服函数，即

(5)

式中：σ1，σ3分别为岩土体剪切面上的第一、第三主应力；c，φ分别为岩土体的黏聚力和内摩擦角.

两种施工方法在开挖过程中，上部掌子面中心点的应力变化情况如图7所示.两种方法在随着开挖面接近上部中心监控位置，球应力都逐渐增大，同时偏应力也逐渐增大.其中，台阶法的应力点向屈服面接近，但并没有达到屈服线，掌子面处于稳定状态和短期稳定状态.而新意法由于施工时对掌子面进行植入锚杆并注浆处理，改善了开挖面前方的岩土体物理力学性质，应力点则超过原有的屈服面，但应力变化并处于弹塑性阶段，即掌子面处于稳定状态和短期稳定状态.

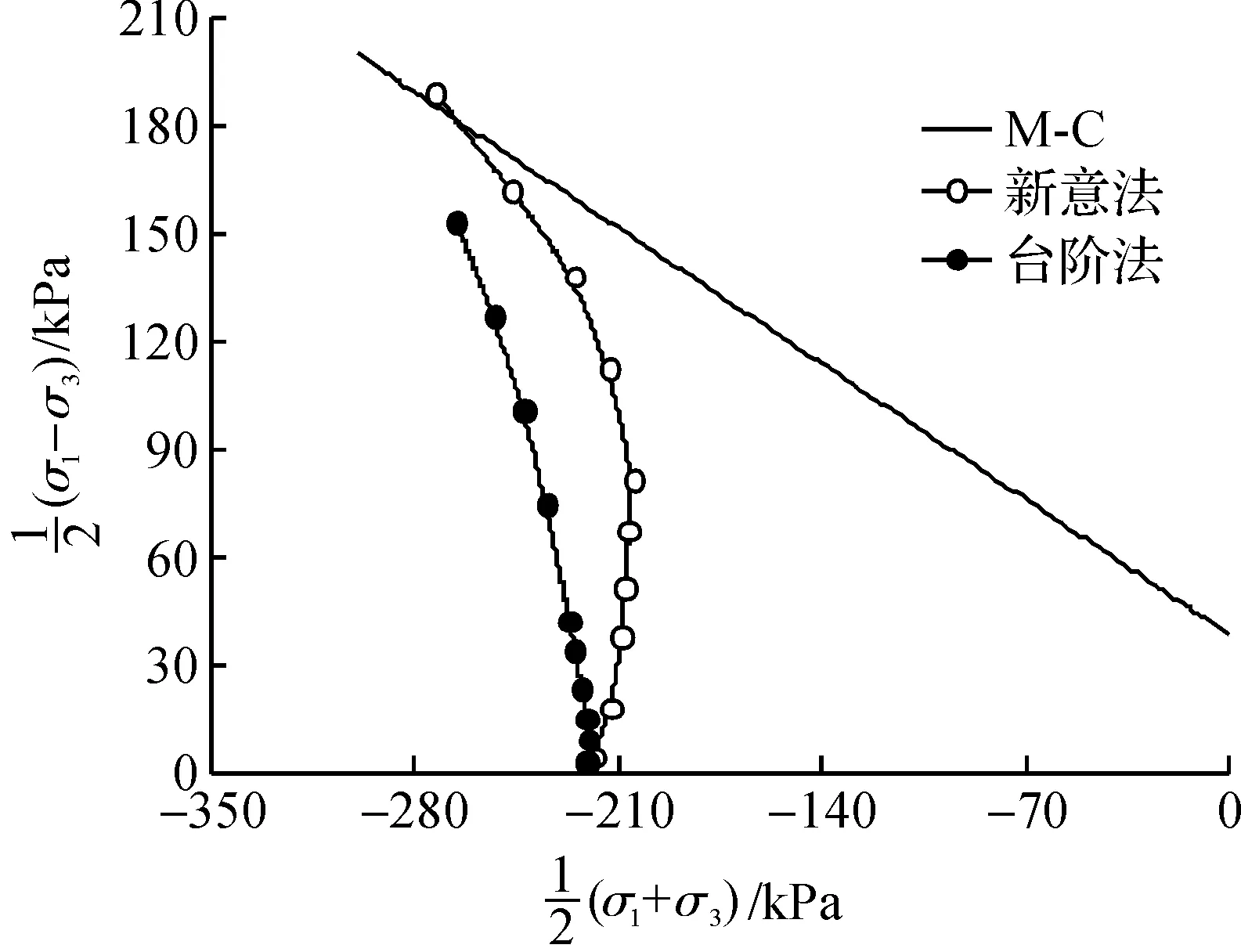
图7 上部掌子面应力变化Fig.7 Face stress of upper face

中部掌子面随着开挖，其中心区域应力变化情况如图8所示.中部掌子面的监控点应力随着开挖面的推进，两种开挖方法的球应力都逐渐减小，而剪应力变化出现差异.台阶法在开挖面距监控点4m时，剪应力几乎不随球应力的减小发生变化，当开挖面距监控点2m时，围岩应力达到M-C屈服线而进入塑性状态，即掌子面失稳.而新意法开挖过程中，其应力点超过了M-C屈服线，但围岩应力并没有发生明显的屈服现象.计算表明，由于隧道所处地层软弱，开挖面前方2m范围内的土体难以维持平衡状态，而通过对开挖面的超前核心土进行加固，可以增强开挖面前方2m内的岩土体的稳定性.

图8 中部掌子面应力变化Fig.8 Face stress of middle face

下部掌子面随着开挖，其中心区域应力变化情况如图9所示.台阶法的监控点应力变化情况和中部掌子面类似，在开挖面距监控点4m时，剪应力几乎不随球应力的减小发生变化，当开挖面距监控点2m时，围岩应力达到M-C屈服线而进入塑性状态，即掌子面失稳.而新意法开挖过程中，球应力和剪应力都在逐渐增大，其应力点超过了M-C屈服线，但围岩应力点并没有完全进入塑性阶段.由图9可知，新意法施工时掌子面更稳定.

3.3 拱顶沉降分析

沿隧道轴线方向每2m选取一个截面，各截面拱顶的最终竖向位移如图10所示，同时选取沿隧道轴线方向上的拱顶特征点的沉降值进行对比分析如表3所示.

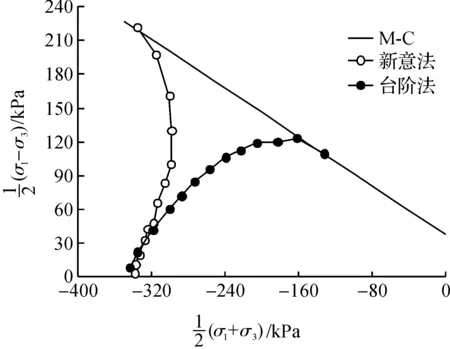
图9 下部掌子面应力变化Fig.9 Face stress of lower face

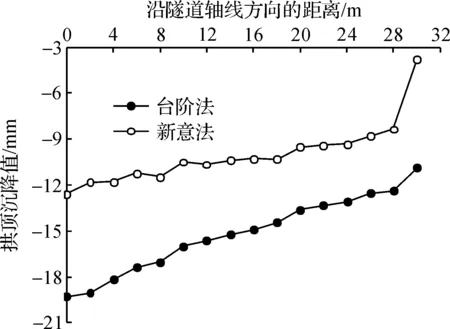
图10 拱顶沉降曲线Fig.10 Result of vault settlement

施工工法拱顶特征点位置/mmY=0mY=6mY=12mY=18mY=26mY=28mY=30m台阶法-19．3-17．38-15．65-14．45-12．53-12．40-10．88新意法-13．10-11．88-10．66-10．31-8．81-8．36-3．62减小比率/%32．132．131．928．729．732．666．7

由图10和表3可知：两种工法开挖隧道完工后，其拱顶竖向位移量均沿着隧道轴线方向逐渐减小.但新意法施工各断面的拱顶沉降量均比台阶法开挖时小，且变化趋势更平缓.此外，新意法开挖时拱顶的最大竖向位移比台阶法的最大竖向位移小了32.1%，且新意法掌子面拱顶处的弹性收敛较台阶法减小了66.7%.由此可见，新意法采用全断面开挖，减少了施工工序，使隧道围岩更快地形成闭合圈，同时结合其超前加固工艺技术，有效地抑制了隧道拱顶的沉降.

3.4 掌子面加固区长度的影响

以新意法掌子面中部挤出位移作为指标对加固区效应进行分析，掌子面中部的挤出位移在不同加固区长度下的变化情况如图11所示.

由图11可知：1) 随着加固区长度的增加，掌子面的纵向位移逐渐减小，且其变化幅度也在逐渐减小，其中加固区长度在8 m以内时，纵向位移变化幅度较大，当超过12 m时，纵向位移曲线变化趋于平缓.对于本隧道出口段，加固区比较适宜的长度是1倍开挖跨度(12 m)，当超过这个距离时，加固区的扩大对于掌子面稳定性影响相对较弱；2) 野猪山隧道出口段处于较为软弱的地层，开挖过程中掌子面易发生失稳破坏，而通过植入全粘结型玻璃纤维锚杆并加压注浆的施工工艺，改变了开挖面处超前核心土的物理力学性质，在一定程度上增强了掌子面的稳定性.

图11 加固区长度对纵向位移影响Fig.11 The effect of reinforcement length on the face stability

4 实测数据与模拟结果对比分析

新意法施工现场YK60+280断面(Y=5 m)和YK60+285断面(Y=0 m)实测的拱顶沉降随开挖时间变化曲线如图12所示.由图12可知：由于280断面初始监测晚，使得拱顶沉降实测值受到较大的影响，280断面拱顶沉降的实测值比285断面的实测值小了近一半.由此可知，初始监测时刻对监测数据量值有较大的影响，且285断面拱顶沉降的实测值更接近实际收敛变形.其中，实测拱顶沉降值在开挖后5～10 d内出现回缩现象是因为掌子面停滞施工时降雨导致浅埋的土体软化、掌子面剥落造成部分围岩应力释放，而YK60+280断面在开挖25 d左右时拱顶沉降值出现回缩现象，是由于施工现场监测的后视棱镜松动导致的.

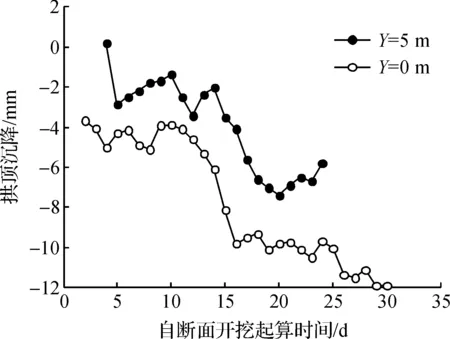
图12 拱顶沉降监测结果Fig.12 Monitoring result of vault settlement

隧道围岩的竖向变形包括了预收敛和收敛变形，该监测项目只能对围岩的收敛变形数据进行采集.由285断面(Y=0 m)的监测结果可知，隧道最终拱顶沉降约为11.88 mm.由数值仿真模拟的计算结果可知，掌子面植入锚杆并注浆加固后，掌子面处拱顶沉降为3.62 mm，285断面(Y=0 m)的模拟沉降为13.10 mm，其中围岩预收敛变形为3.62 mm，收敛变形为9.48 mm左右，模拟值与实测值相差较小，模拟值比实测值小20.2%.由于现场施工过程影响因素较多，模拟值与实测值虽存在一定偏差，但基本吻合.现场监测数据较好地验证了该数值仿真模型的可行性.

5 结 论

通过野猪山隧道出口段数值模拟，对比分析新意法和台阶法下隧道掌子面应力变化和拱顶的沉降，结果表明：野猪山隧道台阶法施工时，尽管开挖循环进尺较小，但掌子面挤出位移较大，其中部极易发生塑性变形，进行围岩周边加固的单一技术措施并不能有效控制掌子面的变形；台阶法开挖时，掌子面前方2 m范围内的土体稳定性问题突出，而新意法的超前加固措施使掌子面前方土体强度发生改变，有效抑制了掌子面失稳；新意法通过对掌子面植入锚杆并注浆加固，改变了超前核心土的强度和刚度，其中加固区比较适宜的长度是1倍开挖跨度；通过对比掌子面稳定性、挤出位移和拱顶沉降量，表明在浅埋软弱地层等特殊工程环境下新意法施工相比于台阶法更为合理.

[1] 姚军，王国才，陈祥林.地应力释放对隧道围岩稳定性影响的研究[J].浙江工业大学学报，2010，38(6)：629-632.

[2] 王克忠，程青云，王玉培，等.粉质砂性土地基中盾构区间隧道开挖过程数值计算研究[J].浙江工业大学学报，2012，40(5)：587-590.

[3] 周艺，何川，邹育麟，等.破碎千枚岩隧道施工工法比选试验研究[J].岩石力学与工程学报，2013(3)：537-548.

[4] 赵录学.关于新意法隧道设计的几点建议[J].现代隧道技术，2012(1)：50-52.

[5] 喻军，刘松玉.隧道洞口边坡变形控制与数值分析[J].浙江工业大学学报，2012，40(1)：101-105.

[6] TONON F. ADECO full-face tunnel excavation of two 260 m2tubes in clays with sub-horizontal jet-grouting under minimal urban cover[J]. Tunnelling and underground space technology, 2011, 26(2): 253-266.

[7] TONON F. Sequential excavation, NATM and ADECO: what they have in common and how they differ[J]. Tunnelling and underground space technology, 2010, 25(3): 245-265.

[8] 潘昌实.隧道力学数值方法[M].北京：中国铁道出版社，1995.

[9] 罗禄森，王明年，郭军.浅埋黄土隧道破坏模式的探讨[J].现代隧道技术，2008(4)：28-31.

[10] 扈世民，张顶立，李鹏飞，等.大断面黄土隧道初期支护适应性研究[J].岩土力学，2011(S2)：660-665.

[11] 周艺.隧道掌子面稳定性分析及其控制技术研究[D].成都：西南交通大学，2010.

[12] YOO C, SHIN H K. Deformation behaviour of tunnel face reinforced with longitudinal pipes-laboratory and numerical investigation[J]. Tunnelling and underground space technology, 2003, 18(4): 303-319.

[13] 陈明祥.弹塑性力学[M].北京：科学出版社，2007.

(责任编辑：刘 岩)

An application study on the ADECO-RS approach in the construction of Yezhu mountain tunnel

WANG Kezhong1, ZHU Haibin1, KONG Lingmin2, LIANG Qidong2, ZHANG Haijun1

(1.College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China; 2.Watersupply Management Office of Rizhao, Rizhao 276800, China)

In order to study the applicability of the ADECO-RS approach in tunnel construction under complicated geological conditions, numerical simulations are used to study the variations of the longitudinal deformation and the stress of faces. The spatial-temporal variations of the vault subsidence along the axial direction are predicted with the ADECO-RS approach and the bench method for the outlet section in the mountain tunnel. The effects of the excessive displacement and instability on the faces between different methods of excavation and temporary reinforcement are analyzed. This indicates that the middle part of the face is liable to lose stability and the ADECO-RS approach can control the deformations effectively. This study is of theoretical and practical significance for the construction of similar tunnels.

ADECO-RS approach; bench method; heading face; numerical modeling

2016-09-27

国家自然科学基金面上资助项目(51679215)；清华大学水沙科学与水利水电工程国家重点实验室开放基金(sklhse-2014-C-02)

王克忠(1965—)，男，山东冠县人，教授，研究方向为隧道工程，E-mail:wkz@zjut.edu.cn.

U459.2

A

1006-4303(2017)03-0237-06