微型桩设计参数对土坡稳定影响的三维数值分析
2017-06-28朱益军王金昌张振宇
施 颖,王 浩,朱益军,王金昌,张振宇
(1.浙江工业大学 建筑工程学院,浙江 杭州 310014;2.浙江交工集团股份有限公司 设计分公司,浙江 杭州 310051;3.浙江大学 交通工程研究所,浙江 杭州 310027)
微型桩设计参数对土坡稳定影响的三维数值分析
施 颖1,王 浩1,朱益军2,王金昌3,张振宇1
(1.浙江工业大学 建筑工程学院,浙江 杭州 310014;2.浙江交工集团股份有限公司 设计分公司,浙江 杭州 310051;3.浙江大学 交通工程研究所,浙江 杭州 310027)
微型桩是加固土质边坡的一种常用工程措施.大多数关于微型桩加固边坡的二维数值分析方法存在一定局限性.结合典型边坡算例,利用岩土工程专业有限元软件Plaxis建立三维数值模型,研究微型桩-土坡体系中设桩位置、桩倾角和桩长等微型桩主要设计参数对边坡稳定性的影响.研究结果表明:微型桩设桩位置对边坡加固效果影响显著,其中设桩在坡中靠下位置时,加固效果最好,设桩在坡顶或坡脚位置,加固效果都不明显;对于土质边坡,微型桩加固边坡存在最优设桩倾角;边坡的安全系数随微型桩桩长L增大而增大,当L达到最佳锚固长度时,桩长变化不再对安全系数产生.
微型桩;土坡;三维数值模型;临界滑动面
由于微型桩及其组合结构具有结构简单、施工方便、造价较低以及适用范围广等特点,近年来广泛应用于边坡加固等防护工程中并取得了良好的加固效果和经济效益[1].如何将微型桩更安全有效地用于边坡加固,多年来专家和学者倾注了大量心血同时取得了丰富的研究成果.通过文献检索发现,有关微型桩的研究内容大体可以分为3类:1) 理论分析.基于传统力学理论建立数学模型,研究桩土间荷载传递机制或相互作用机理[1-3];2) 数值模拟.利用数值计算软件建立二维或三维模型,分析桩-土相互作用下桩身的受力和变形,以及桩间土的应力和变形情况[4-8];3) 模型试验.通过室内离心实验或模型试验等,直观研究桩-土作用机理及桩的工作性能[9-11].
上述几类研究工作中,得益于计算机技术的快速发展,数值模拟分析方法在微型桩加固边坡的研究中扮演了越来越重要的角色,诸多研究成果有效提升了微型桩加固边坡的合理性.然而,综合相关资料,笔者注意到微型桩数值分析大多采用二维模型,而边坡实际破坏一般呈现三维特征,二维数值模型往往不能真实反映边坡的真实状态和失稳过程[4].因此,结合典型算例边坡,利用岩土专用有限元软件Plaxis建立三维数值模型,分析微型桩设桩位置、桩倾角和桩长等微型桩主要设计参数对边坡稳定性及临界滑动面的影响,以期为微型桩加固边坡工程提供指导和借鉴.
1 边坡稳定有限元分析方法
利用有限元法分析复杂边坡的稳定性,考虑了岩土材料的非线性弹塑性本构关系和边界条件的复杂性,能够有效模拟岩土材料应力应变关系,分析边坡破坏的发生和发展过程,具有传统的极限平衡法所达不到的优点,目前在工程中得到广泛应用.
1.1 强度折减法
Duncan[12](1996)指出,边坡的安全系数F可以定义为使边坡刚好达到临界状态时,岩土材料抗剪强度的折减程度,即岩土实际抗剪强度与临界破坏时抗剪强度的比值,具有强度储备的性质.因此,当坡体处于临界状态时,岩土体的临界抗剪强度参数c′,φ′可以表示为
(1)
式中:c,φ分别为岩土所能实际发挥的抗剪强度.
岩土抗剪强度折减的变化过程可以用Morh应力圆来说明,如图1所示.抗剪强度折减的过程就是抗剪强度包络线与Mohr应力圆相切的过程,当两者相切时对应的折减系数F即为边坡的安全系数.
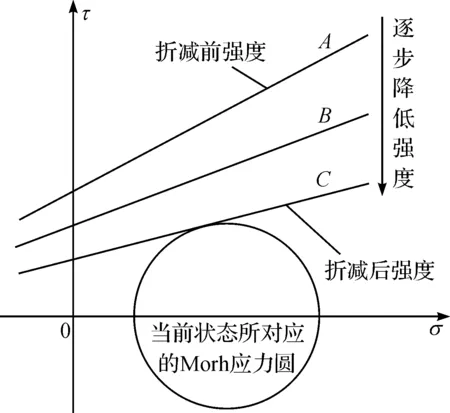
图1 抗剪强度折减原理Fig.1 Shear strength reduction principle
1.2 边坡失稳判据
如何判别边坡是否处于整体失稳状态是边坡有限元稳定分析的一个关键问题.目前,边坡失稳破坏的判据主要有以下几种[13]:
1) 坡体内塑性区贯通.
2) 坡体滑移面上应变和位移发生突变且无限发展.
3) 有限元计算不收敛.
按照岩土力学中的破坏准则,边坡失稳破坏时,滑面上每点的应力应变都达到极限平衡状态,材料进入破坏状态同时模型计算不能收敛,此时岩土体抗剪强度得到充分发挥,由此可依据强度折减法得到边坡的安全系数.因此,有限元分析时采用力或位移计算不收敛作为边坡失稳的判据是比较合理的.
2 三维模型的建立
参考典型边坡算例,结合研究目的,建立边坡-桩模型侧面、平面图见图2.其中模型底面长40m,左侧高22.5m,右侧高10m,边坡坡高为12.5m,坡面水平长度15m,坡度40°.微型桩桩长L=7.0 m,桩径D=0.6 m,桩间距S=3.0 m.为更直观显示边坡在强度折减后的变形破坏情况,根据图1建立Plaxis双桩三维有限元模型,划分单元网格后如图3所示.对计算模型x轴方向左右两侧边界位移约束,y轴方向前后两侧边界位移约束,底部三向边界位移约束.土体采用服从Mohr-Coulomb破坏准则与非相关联流动法则的理想弹塑性本构模型.桩-土间设置相互接触作用,摩擦因数为0.4.采用软件自带的强度折减法计算边坡的安全系数,微型桩、土体的材料参数见表1.
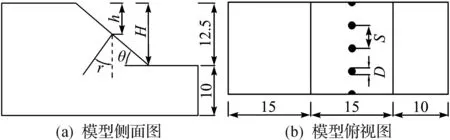
图2 边坡-微型桩模型平面图Fig.2 Plan of slope-micropile model

图3 微型桩加固边坡三维有限元模型Fig.3 3D numerical model of slope
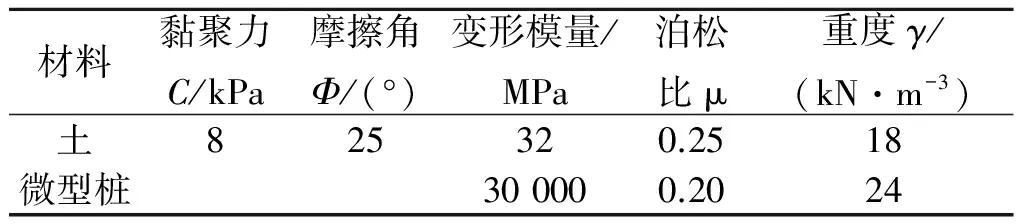
材料黏聚力C/kPa摩擦角Φ/(°)变形模量/MPa泊松比μ重度γ/(kN·m-3)土825320.2518微型桩300000.2024
3 分析与讨论
3.1 设桩位置对边坡稳定性的影响
针对微型桩加固边坡设桩位置问题,取微型桩倾角r=0°,r=40°(即竖直放置、垂直于坡面)两种形式分别建立计算模型.变化微型桩位置计算得到h/H与边坡安全系数F的变化曲线如图4所示.分析这三条曲线,随着h/H的增大即设桩位置往下移时,安全系数F先增大后减小;当h/H=0.6时,F达到最大值,即设桩在坡中靠下位置时,微型桩对边坡的加固效果最好;设桩于坡顶时,加固效果不明显;设桩于坡脚时,微型桩几乎起不到加固效果.对比桩加固的两条曲线,可以发现斜桩-边坡体系的稳定性要高于直桩-边坡体系的稳定性,且在微型桩位于坡中靠下位置时,两者差距更加明显,说明设桩倾角对加固边坡的安全系数有较大影响.
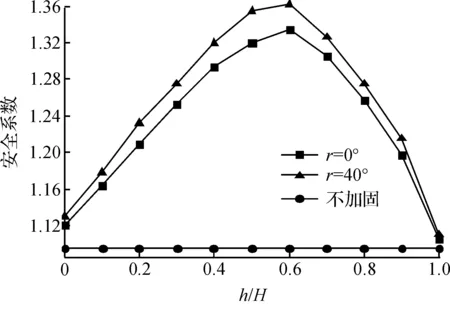
图4 边坡安全系数与设桩位置关系图Fig.4 Relationship between FOS and micorpile locations
图5显示为设桩位置不同时(r=40°),边坡经强度折减后临界滑动面的分布情况.从图5可以看出:当微型桩位于坡顶或坡脚时,边坡临界滑动面靠近坡表,说明此时微型桩阻滑作用不大,边坡稳定性较低;随着设桩位置往下移动,微型桩阻滑作用加强,滑动面由浅层向深层转变,表明边坡的稳定性逐渐提高;当设桩在h/H=0.6时,微型桩承受最大的桩后土推力,同时临界滑动面处于坡体最深处,表明此时边坡最稳定,微型桩加固效果最好.此外,设桩在坡脚时,塑形应变区显示为完整的贯通弧面,说明此时的微型桩几乎没有起到阻滑作用.以上分析可以发现临界滑动面的变化规律与安全系数随设桩位置的变化规律相一致.
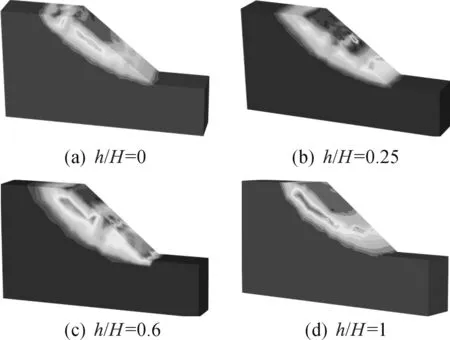
图5 不同设桩位置时边坡临界滑动面Fig.5 Critical slip surface at the different micropile locations
3.2 设桩倾角对边坡稳定性的影响
由前述分析,对于坡体强度较低的土坡,传统的竖直设桩并非最佳方式,微型桩倾角对加固边坡的安全系数有明显影响.因此基于图3模型,设桩于h/H=0.6处,变化桩倾角r研究其对边坡安全系数的影响规律.图6为桩倾角r与边坡安全系数F的关系曲线图.从图6中可以看出:当r在0~60°区间内,F先增大后减小.对于该坡度为40°的土质边坡,要使微型桩发挥最大的阻滑作用,最优设桩倾角约为30°.

图6 边坡安全系数随微型桩倾角变化曲线图Fig.6 Effects of micorpile inclination on FOS
图7显示为设桩在h/H=0.6处时边坡的临界滑动面分布图.可以发现设桩在此位置时,微型桩都将滑动面分成了前后两个部分,说明微型桩起到了有效的阻滑作用.对比各图7可知:当桩倾角r=30°,滑动面深度明显最深,说明此时边坡最为稳定.

图7 不同设桩倾角时边坡临界滑动面Fig.7 Effects of micropile inclination on critical slip surface
3.3 微型桩桩长对边坡稳定性的影响
采用前述算例参数,取桩倾角r=20°,变化微型桩长度L计算得到其与安全系数F的关系曲线见图8.从图8可以看出:当L≤5 m时,安全系数变化不明显;当5 图9显示为临界滑动面分析桩长对边坡稳定性的影响.从图9可以看出:桩长L=4 m和L=5 m时边坡的临界滑动面深度没有变化,塑形应变区显示为贯通的弧面,说明桩长过小时加固效果不理想;当L≥6 m时,一方面临界滑动面不断向坡体内部深入,另一方面微型桩对塑形应变区的阻隔作用逐渐加强,说明微型桩逐步提高边坡的稳定性;这与图8显示的桩长与安全系数的变化规律一致;当L≥10 m时,微型桩完全阻隔了塑形应变区的发展,此时增大桩长不再影响边坡稳定性. 图8 边坡安全系数与桩长关系图Fig.8 Relationship between FOS and micorpile length 图9 不同桩长时边坡临界滑动面Fig.9 Effects of micropile length on critical slip surface 利用岩土工程专业有限元软件Plaxis,建立三维微型桩-土坡数值模型,研究微型桩主要设计参数对边坡稳定性的影响.结果表明:将桩设在h/H=0.6处即坡中靠下位置时,微型桩对边坡的加固效果最好;设桩于坡顶时,加固效果不明显;设桩于坡脚时,微型桩几乎起不到加固效果;边坡临界滑动面的变化规律与安全系数随设桩位置的变化规律相一致;对于土质边坡,传统的竖直设桩并非最佳方式,微型桩加固边坡时存在最优设桩倾角;微型桩桩长L过小时,对加固边坡稳定性的影响很小;当L在一定区间时,安全系数快速增长同时关系曲线斜率缓慢减小;当L达到最佳锚固长度时,桩长变化不再对边坡安全系数产生影响. [1] 陈立新,王士川.抗滑桩的弹塑性理论分析[J].工业建筑,1997,27(7):28-33. [2] 高永涛,张友葩,吴顺川.土质边坡抗滑桩机理分析[J].北京科技大学学报,2003,25(2):117-123. [3] 杨雪强,吉小明,张新涛.抗滑桩桩间土拱效应及其土拱模式分析[J].中国公路学报,2014,27(1):30-37. [4] 张克利.基于强度折减有限元法的三维边坡稳定性与破坏模式分析[D].大连:大连理工大学,2011. [5] 年廷凯,徐海洋,刘红帅.抗滑桩加固边坡三维数值分析中的几个问题[J].岩土力学,2012,33(8):2521-2526. [6] 张友良,冯夏庭,范建海,等.抗滑桩与滑坡体相互作用的研究[J].岩石力学与工程学报,2002,21(6):839-842. [7] 杨伟,丁伯阳,潘晓东,等.基于GIS的边坡三维稳定性计算[J].浙江工业大学学报,2012,40(1):92-95. [8] 丁伯阳,陶海冰,周乐尧.富阳长绿镇青龙山滑坡治理[J].浙江工业大学学报,2004,32(2):52-57. [9] 叶海林,郑颖人,李安洪,等.地震作用下边坡抗滑桩振动台试验研究[J].岩土工程学报,2012,34(2):251-257. [10] 欧孝夺,唐迎春,崔伟,等.h型抗滑桩模型试验及数值模拟[J].岩石力学与工程学报,2012,31(9):1936-1943. [11] 戴自航.抗滑桩滑坡推力和桩前滑体抗力分布规律的研究[J].岩石力学与工程学报,2002,21(4):517-521. [12] 陈祖煜.岩质边坡稳定分析[M].北京:中国水利水电出版社,2003. [13] 郑颖人,赵尚毅,宋雅坤.有限元强度折减法研究进展[J].后勤工程学院学报,2005,3(3):1-6. (责任编辑:刘 岩) Three-dimensional numerical analysis for the effect of micropile parameters on the stability of slopes SHI Ying1, WANG Hao1, ZHU Yijun2, WANG Jinchang3, ZHANG Zhenyu1 (1.College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China; 2.Design Branch of Zhejiang Communications Construction Group Co., Ltd., Hangzhou 310051, China; 3.Institute of Traffic Engineering, Zhejiang University, Hangzhou 310027, China) Micropiles are commonly used to reinforce soil slopes. Due to the limitation of two-dimensional numerical analysis, a typical slope example is selected and the Plaxis is adopted to establish a 3D model of the micropile-soil slope system to analyse the position, inclination, length of micropiles on the stability of slopes. The results show that, when the micropile is placed a place which is slightly lower than the middle of the slope, the reinforcing effect is the best. However, when the micropile is placed at the top or foot of the slope, the reinforcing effect is not obvious. For soil slopes, the micropile has an optimum inclination. The factor of safety of slopes increases with the increase of the micropile lengthL. When the length is too large, the micropile has no effect on the stability of slopes. micropile; soil slope; three-dimensional numerical model; critical slip plane 2016-11-03 浙江省科技计划项目(2015C31006);浙江省交通运输厅科技计划项目(2016H06,2014H27) 施 颖(1963—),男,浙江兰溪人,教授级高级工程师,博士,研究方向为桥梁结构设计和理论研究,E-mail:zj_sy2003@163.com. U416.14 A 1006-4303(2017)03-0249-04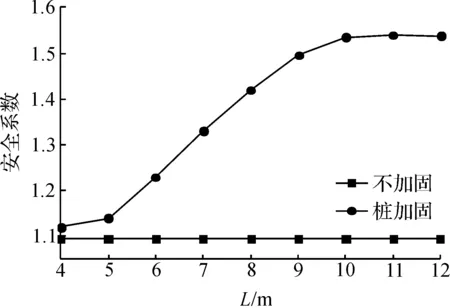

4 结 论
