任意光滑曲面上静止均质链所需拉力与总支持力的计算
2017-06-27曹鹏李力
曹 鹏 李 力
(1. 重庆市实验中学,重庆 401320; 2. 重庆市清华中学,重庆 400054)
任意光滑曲面上静止均质链所需拉力与总支持力的计算
曹 鹏1李 力2
(1. 重庆市实验中学,重庆 401320; 2. 重庆市清华中学,重庆 400054)
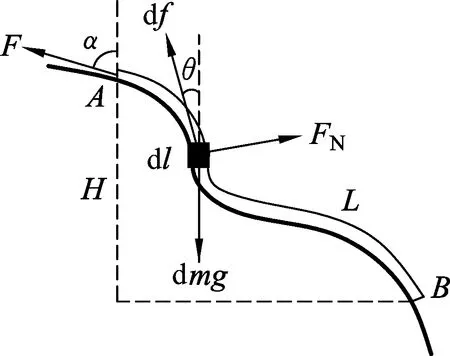
图1
一长度为L、线密度为λ的均质链AB,放在竖直面内任意形状的光滑曲面上,如图1所示.若要其静止,则沿链顶端A的切线方向,应施加多大的拉力F?
可研究链上任意一处质量为dm的微元dl,设其与竖直方向成θ角,其上、下端所受张力分别为(f+df)与f,都在该处的切线上但彼此反向,二者合力则沿切线向上,大小为df=(f+df)-f,故该微元受力如图1所示.由切向上的平衡,有df=dm·gcosθ=λg·dl·cosθ,沿整条链积分可得

(1)
其中H是链条AB在竖直方向上的投影总高度.文献[1]用以上方法证明了这个有趣的结论,下面我们另外给出一个更简洁的证明.
设想在拉力F作用下,链条沿曲面向上缓慢移动很小的距离ds.比较均质链的初末状态,可以看出,相当于把微元ds从下端B移至上端A而已.由功能原理可得F·ds=λds·gH,化简即为(1)式.
其实,还可以进一步拓展研究整根链条所受光滑曲面给予的总支持力,也可以找到简洁的计算公式,这在文献[1]中并没有提及.

图2
假设沿链条顶端A的切向与竖直方向夹角为α,链的总长为L,则不难求出均质链所受总支持力N的大小和方向.
如图2,整根均质链在重力G、拉力F和支持力N作用下静止,设N与竖直方向夹角为β,又G=λgL,F=λgH,代入余弦定理N2=G2+F2-2GFcosα得

(2)

(3)
从(1)式可知,任意光滑曲面上均质链静止所需拉力F的大小,只取决于上下端点之间的竖直距离H;其所受总支持力N的大小和方向,都与链条全长L、F与竖直方向的夹角α以及H有关,式(1)~(3)是一般计算公式,与光滑曲面的形状无关,这是一个在理论上比较有趣而且有一定实用价值的结果.
1 王伟民,辛存良.对一个力学问题的深入推广[J].物理教师,2016(12):57-59.
2017-01-11)
