关于一道北京大学自主招生(2009年)试题的探讨

孙望涛 胡晓雄

(浙江省长兴中学,浙江 湖州 313100)



关于一道北京大学自主招生(2009年)试题的探讨

孙望涛 胡晓雄

(浙江省长兴中学,浙江 湖州 313100)

1 问题的提出

图1

原题.(2009年北大自主招生试题)如图1所示,光滑的水平桌面上平放着一个半径为R,内壁光滑的固定圆环,质量分别为m、2m、m的小球A、B、C在圆环内侧的位置和速度大小、方向均在图中标出,初始B小球静止,已知所有碰撞为弹性碰撞,试问,经过多长时间,A、B、C3个小球又第1次恢复到原来位置．

此题也出现在文献[1]中，试题和文献[1]中给出的参考答案如下.

参考答案:首先推导两个物体发生弹性碰撞后的通解公式．由系统动量守恒定律得

m1v10+m2v20=m1v1+m2v2，

由碰撞前后动能之和保持不变,有

联立解得

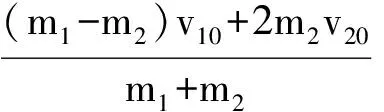
(1)

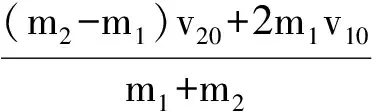
(2)

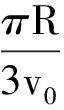
②B与C经历时间t2后发生碰撞,B、C碰后速度通过公式(1)、(2)计算得vB2=v0,vC2=-3v0．

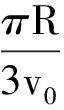
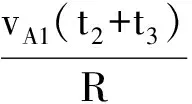
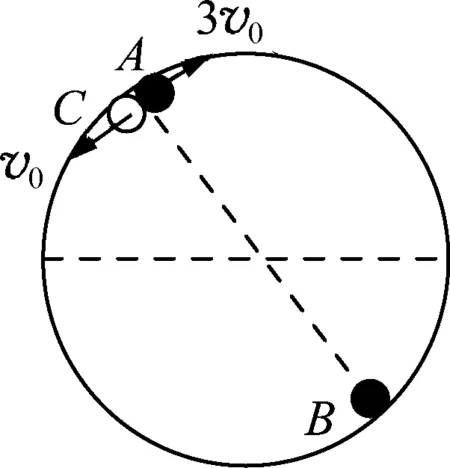
图2

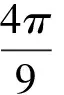
上述解答中每一次碰撞都需将两小球质量、碰前速度代入碰撞通解公式(1)、(2)进行运算,计算量较大,十分繁琐.

2 转换参考系简化解题过程

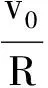
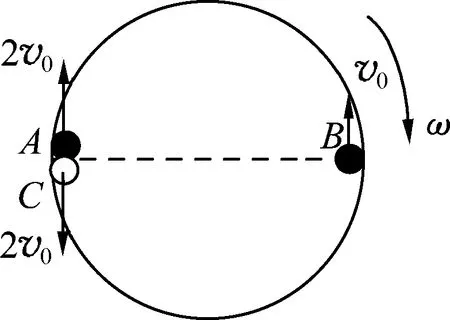
图3

在此参考系中,vA=2v0,vB=-v0,vC=-2v0,我们惊讶地发现,PA=2mv0,PB=2m(-v0)=-2mv0,PC=m(-2v0)=-2mv0,即A、B、C3小球动量大小相等．我们知道,当两个动量大小相等,方向相反的小球发生对心弹性碰撞时,小球碰后反向运动,且速度大小与原速度相等．

于是,本题变得异常简单,我们记碰撞发生的位置相对于A、C起点转过θ．

①A与B相碰．如图4所示，有

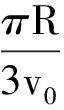
②B与C相碰．如图5所示，有

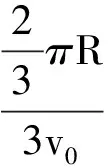
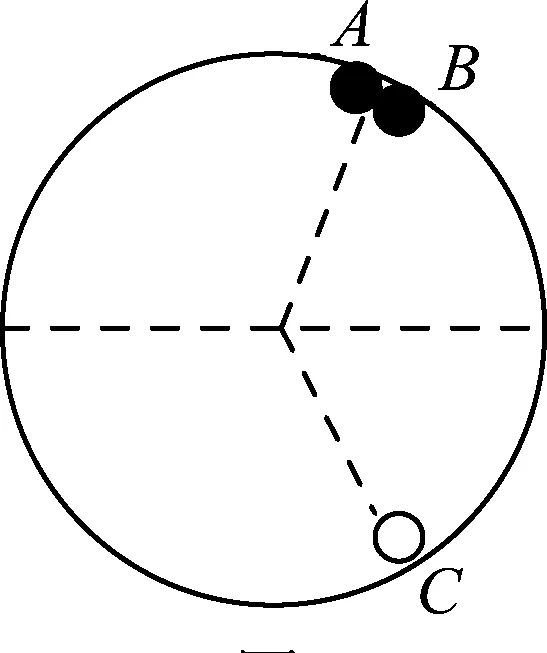
图4

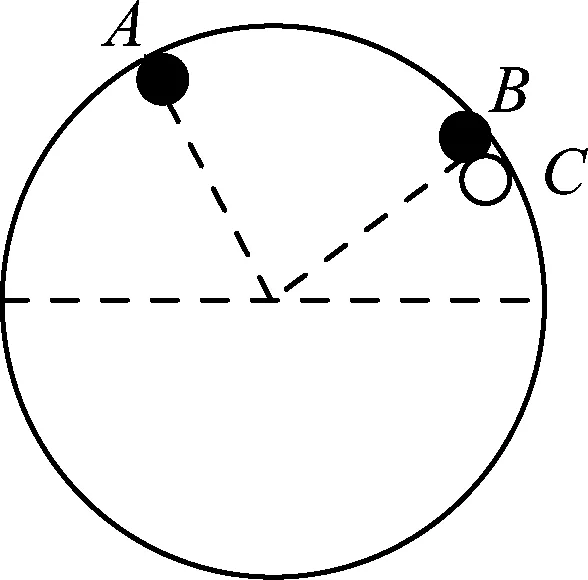
图5

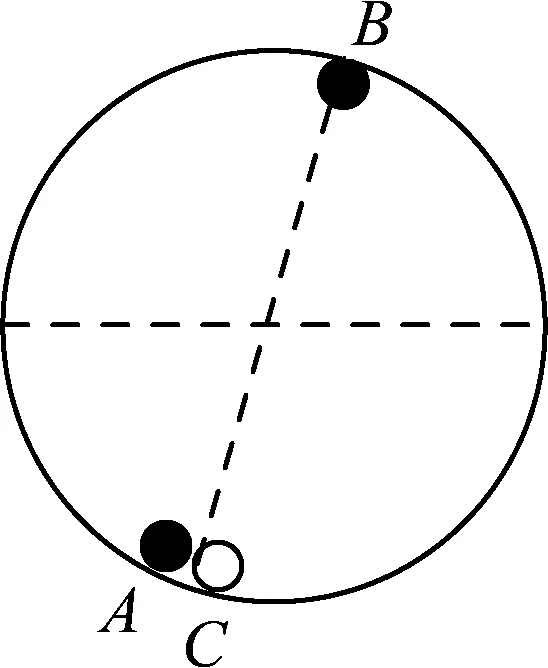
图6

③C与A相碰．如图6所示，有

3 关于问题的进一步探讨

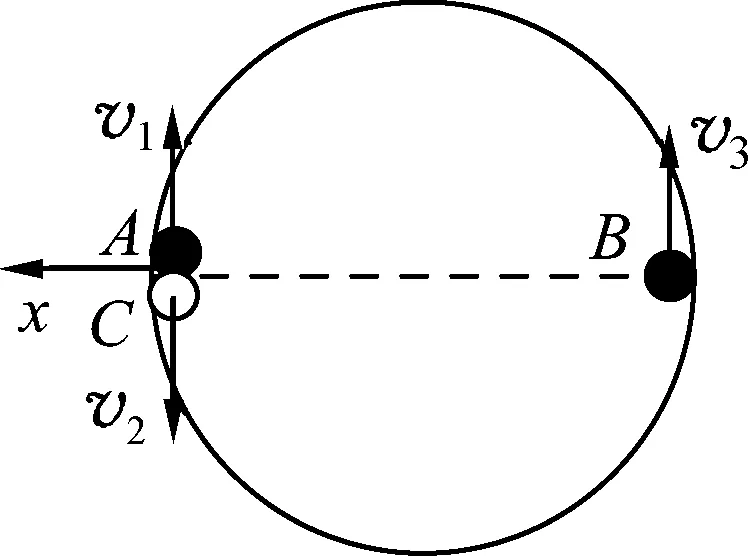
图7

我们再来探讨3球在动量相等的前提下需满足何种条件才能使运动具有周期性．如图7所示,设3小球速率为v1、v2、v3(已满足p1=p2=p3),用θ表示相碰两球相对x轴顺时针转过的角度,θ′表示两球相碰时第3球相对x轴顺时针转过的角度,以下省略大量计算过程．

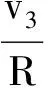
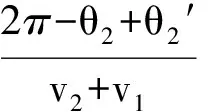
要使3球相对位置回到初态,则θ3=θ3′+π,解得v1=v2．

由此得出结论:如图8所示,任意3个动量大小相等的小球在圆环内发生碰撞,只要初态A、C两球速度大小相等,方向相反,它们的运动具有周期性．

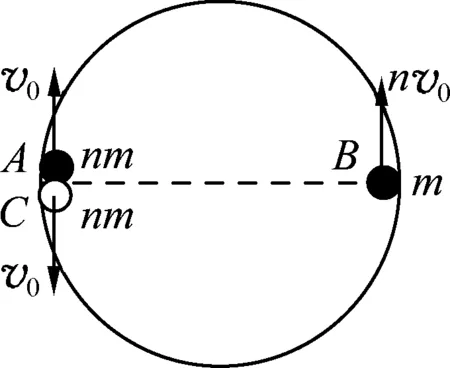
图8 图9

1 江四喜.重点大学自主招生物理培训讲义[M].第3版.合肥:中国科学技术大学出版社,2016:92-93.

2 胡晓雄.对教辅中一道结构不良习题的分析与反思[J].物理通报,2015(6)：45-46.

2017-01-21)