一道静摩擦力试题的多种正解和误解分析

周化海 黄绍书

(六盘水市第23中学,贵州 六盘水 553001)



·复习与考试·

一道静摩擦力试题的多种正解和误解分析

周化海 黄绍书

(六盘水市第23中学,贵州 六盘水 553001)

对网上激烈热议的一道关于静摩擦力的测试题进行详细分析,并给出其多种正确解法及错误解法．同时,对一些相关问题予以说明．

静摩擦力; 分析; 二次旋转; 二面角; 投影面积

1 问题及背景

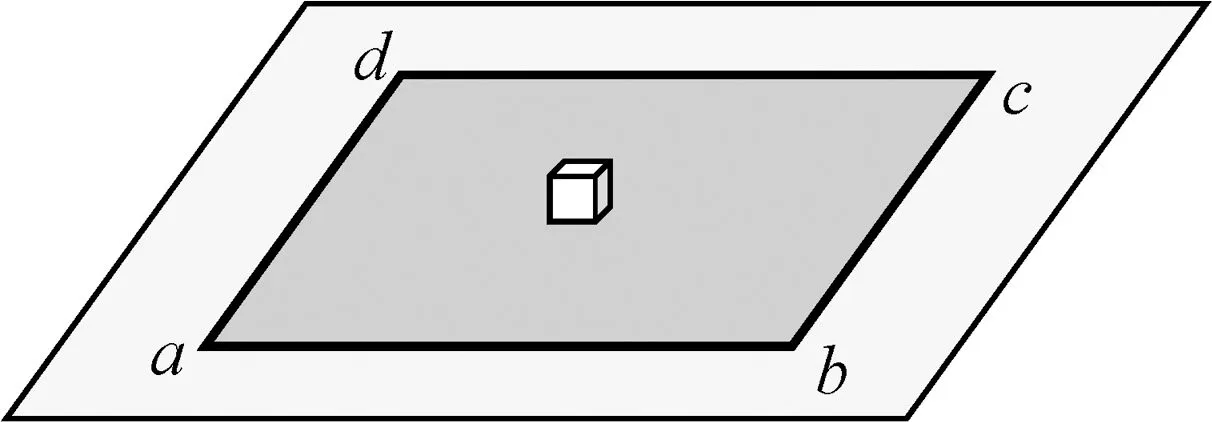
图1

题目.在水平桌面上放置一正方形薄木板abcd,在木板的正中间放一质量为m的木块．先以木板的ad边为轴缓慢将木板转θ角,再以ab边为轴将木板向上缓慢转θ角,如图1所示．整个过程中木块没有滑动,则转动后木块受到的摩擦力大小为

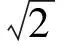
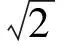
这是网上最近激烈热议的一道关于静摩擦力的测试题．

2 分析的思路

这是一道看似简单,实则是颇具难度的试题．它对数学知识的储备要求较高,必须要有一定的空间想象力和二面角的思维,并能正确求出涉及到的二面角,才能给出正确的结果．

这道练习题的求解关键通常是找出木板经二次旋转之后与水平面之间的夹角,即木板与水平面构成的空间二面角．

3 正确的解析

现将讨论的几种比较好的正确解法进行梳理,以飧读者．

解法1：设木块在初始平面1的位置O到正方形各边的距离为L,则

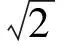
木板第1次绕ad转θ角到平面2,令这时Oa与平面1的夹角为α,如图2所示，那么

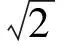
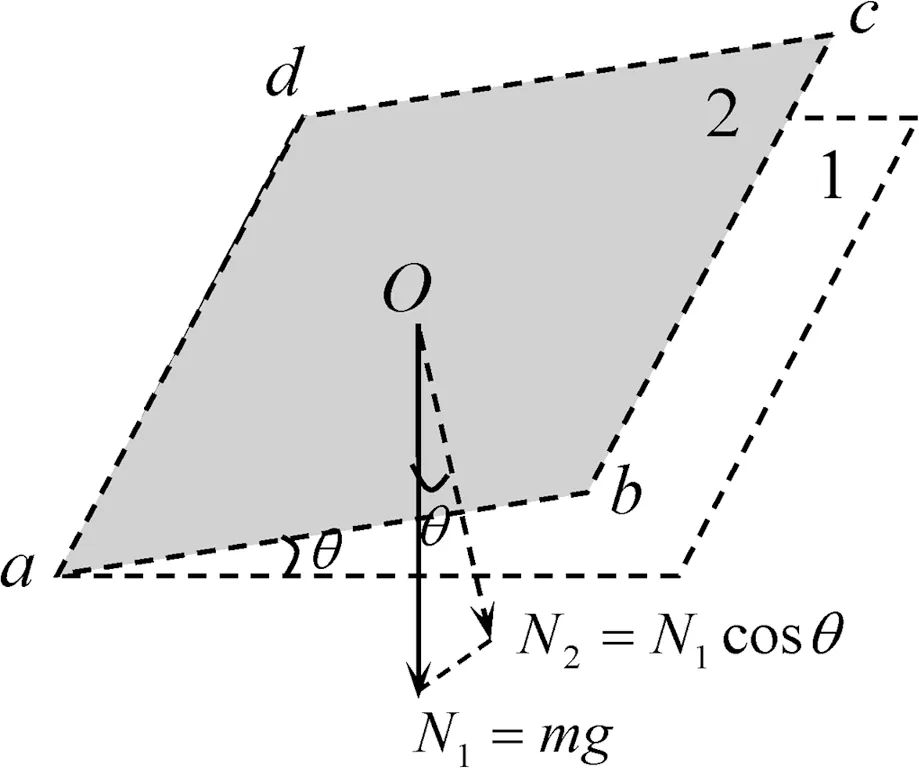
图2

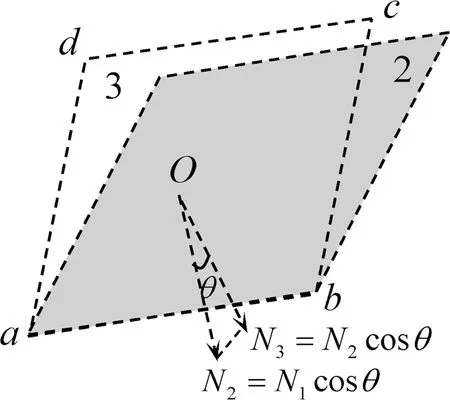
图3

如图3所示，木板第2次绕ab转θ角到平面3时,Oa与平面2的夹角显然亦为α,因此Oa与平面1的夹角必为2α．所以,木块此时受到的摩擦力大小为

f=mgsin2α=2mgsinαcosα=

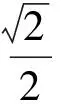
从而,选项(D)正确．

解法2：设木板的初始位置为平面1,并令设正方形的边长为L,则正方形的面积为

S=L2.

木板第1次绕ad转θ角到平面2时,正方形在平面1的投影面积为

S1=Scosθ=L2cosθ.

木板第2次绕ab转θ角到平面3时,正方形在平面2的投影面积亦为

S2=Scosθ=L2cosθ.

因此,此时正方形在平面1的投影面积为

S3=S2cosθ=L2cos2θ.

设平面3与水平面1之间夹角为φ,则有

S3=L2cosφ，

那么

cosφ=cos2θ.

所以,木块此时受到的摩擦力大小为

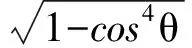
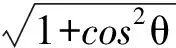
同理,选项(D)正确．

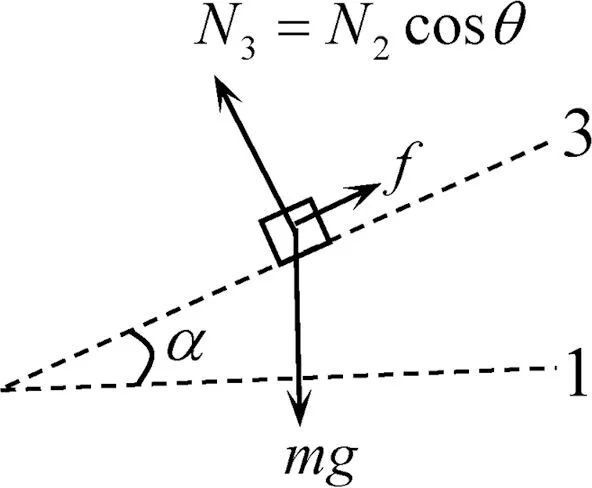
图4

解法3：设木板的初始位置为平面 1，第1次绕ad转θ角的位置为平面2，第2次绕ab转θ角的位置平面3，且平面3与水平面1之间夹角为α．令木块重力在各个平面上的法向投影分别为N1、N2、N3,木块受到的摩擦力为f,如图2—图4所示．那么

N1=mg，

N2=N1cosθ=mgcosθ，

N3=N2cosθ=mgcos2θ.

且N32+f2=(mg)2，

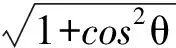
所以,选项(D)正确．

这一解法避开求木板经2次旋转后与水平面之间的夹角α．但求出摩擦力f后,可根据f=mgsinα，

得到平面3与水平面1之间夹角α满足

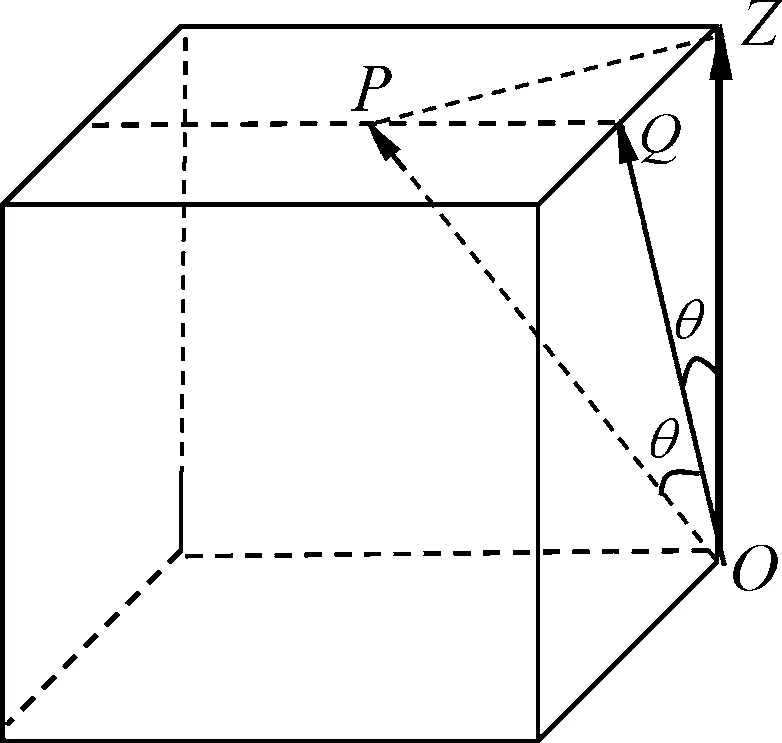
图5

解法4：设木板的初始位置平面的法向量OZ为单位长度1,第1次转动平面时法向量转θ角变为OQ,第2次转动平面时法向量亦转θ角变为OP,如图5所示．令OP与OZ的夹角为α角,那么

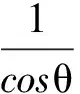
所以

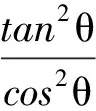
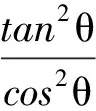
因此

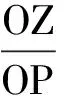
因而,木块此时受到的摩擦力大小为

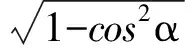
故,选项(D)正确．

这4种解法简繁各异,但都能达到殊途同归的效果．

4 隐蔽的错误

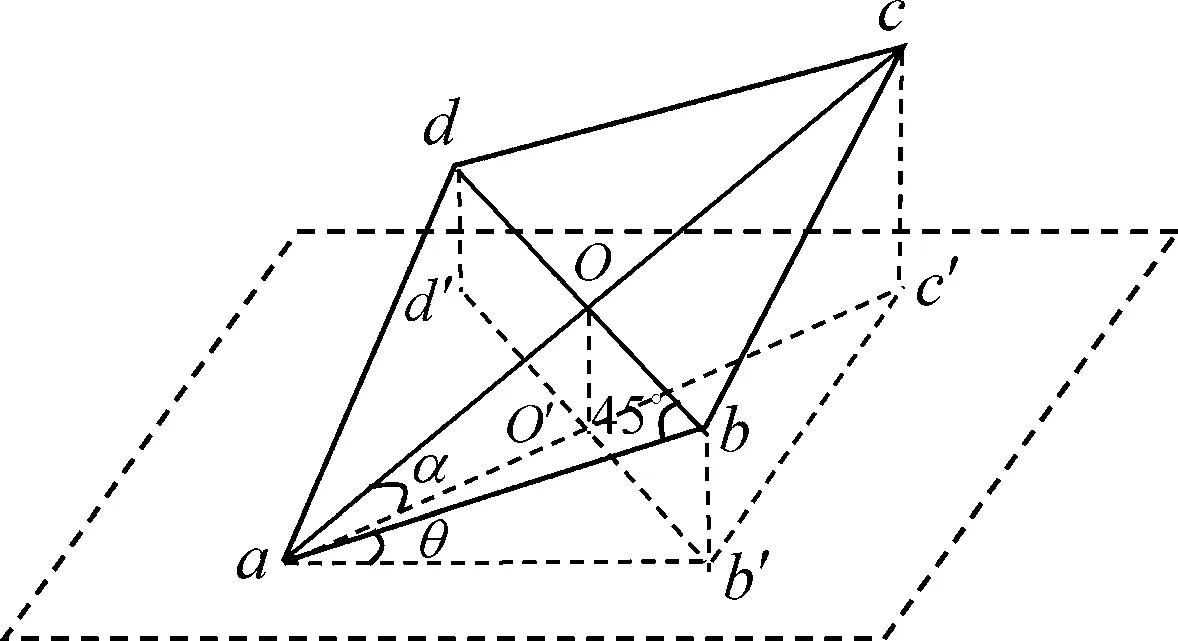
图6

在讨论中,还给出一些比较隐蔽的错误解法,我们摘取其中比较典型的两例,供同行参考,以求共同提高．

错解1：设木板先后绕ad、ab转动θ角之后与水平面之间的夹角为α,如图6所示．那么

因此

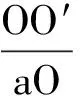
所以,木块受到的摩擦力大小为

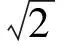
从而得出选项(B)正确．

错解2：设正方形木板的边长为L．那么,木板以ad边为轴将木板转θ角后,则b点比a点高Lsinθ;木板再以ab边为轴将木板转θ角后,同理c点比b点高Lsinθ．令此时ac与水平面之间的夹角α,那么

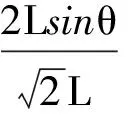
因此,木块受到的摩擦力大小为

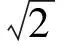
因而,选项(B)正确．

这两种分析方法的错误隐蔽性,在于木板经二次转动之后,均认为正方形的b点与d点等高．

5 思考与结语

物理教学中必须加强应用数学知识解决物理问题的能力培养,这是培养学生物理核心素养的要求所在,这也就要求物理教师有足够的数学知识储备．

众多物理QQ群已经成为物理教师专业发展的网络平台,通过这一平台能使教师的思想和专业素养都较快的提升．

本文是物理QQ群全体教师讨论的结晶,笔者仅是给出其中一种简易解法的谈论者之一．在此,特别感谢四川邓学军老师、湖北许文老师、江西涂德新老师以及北京王小老师的有益讨论．

2017-01-11)