浅析竖直平面内圆周运动中的轨道“离地”临界条件

许 龙 辛淑媛

(1. 安徽省太和县第一中学,安徽 太和 236600; 2. 安徽省太和中学,安徽 太和 236600)



·问题讨论·

浅析竖直平面内圆周运动中的轨道“离地”临界条件

许 龙1辛淑媛2

(1. 安徽省太和县第一中学,安徽 太和 236600; 2. 安徽省太和中学,安徽 太和 236600)

竖直平面内圆周运动最高点模型的使用是需要考虑实际情况,本文将基于一道高考模拟题用数学方法分析最高点的临界状态的使用条件,以及常遇到的将轨道顶起的位置及条件．

最高点模型;数学方法;临界速度;顶起轨道

竖直平面内圆周运动的最高点临界模型是高中阶段最常考的一个知识点,常会考到物块恰好到最高点时的临界速度,轨道压力等问题．但有时候“简单、粗放”地使用最高点模型并不一定会得到正确的结果,必须通过数学手段的分析才能知道在哪种情况下可以使用最高点模型,哪种情况又不能使用．笔者将结合一道高考模拟题来展开论述．

图1

1 真题回放

例题.如图1,A是半径为R的圆形光滑轨道,固定在木板B上,竖直放置;B的左右两侧各有一光滑挡板固定在地面上,使其不能左右运动,小球C静止放在轨道最低点,A,B,C质量相等．现给小球一水平向右的初速度v0使小球在圆型轨道的内侧做圆周运动,为保证小球能通过轨道的最高点,且不会使B离开地面,求初速度v0必须满足的条件(已知重力加速度为g).

1.1 分析解答

最小值很好理解,至少过最高点,则在最高点存在临界条件，有

同时从最低点到最高点,利用动能定理有

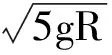
若按照常规思维,在最高点小球对轨道向上的弹力FN与轨道和底座的总重力Mg的关系为

FN≤Mg，

小球对轨道的作用力FN与轨道对小球的作用力FN′是一对相互作用力FN=FN′,最高点向心力为

同时由动能定理有

可得在最低点的速度为

1.2 问题探讨

图2

这样的解答很难让人信服．笔者认为小球将轨道顶起的位置要有所讨论．难道只能在最高点才能把轨道顶起来么?小球到达轨道最高点之前就没有球与轨道的作用力的竖直分力大于轨道和底座重力么?

基于这样的疑问笔者用数学方法分析有没有可能在最高点之外的地方将轨道顶起．

假设在最高点之外的D点可能,此时OD与竖直方向夹角为θ,如图2．此时向心力为

F向=FN′+mgcosθ.

联立可得

而轨道不离地面的条件是球对轨道作用力的竖直向上的分力小于轨道及底盘自重,即

FNcosθ≤2mg.

对不等号右侧可视为cosθ的函数

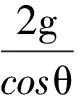
由均值不等式可得

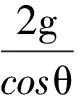
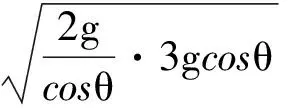
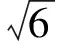
若要此式恒成立则必有

即得

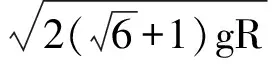
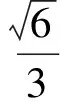
由于0～90°内余弦函数0≤cosθ≤1,此时求得结果正好在此范围内,符合题意．

如果按照答案给的结果的话,在小球没到最高点的时候就已经将轨道顶起来了．

2 问题拓展

设轨道质量M,满足FNcosθ≤Mg，小球未将轨道顶起,进而可以得到

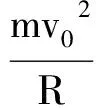
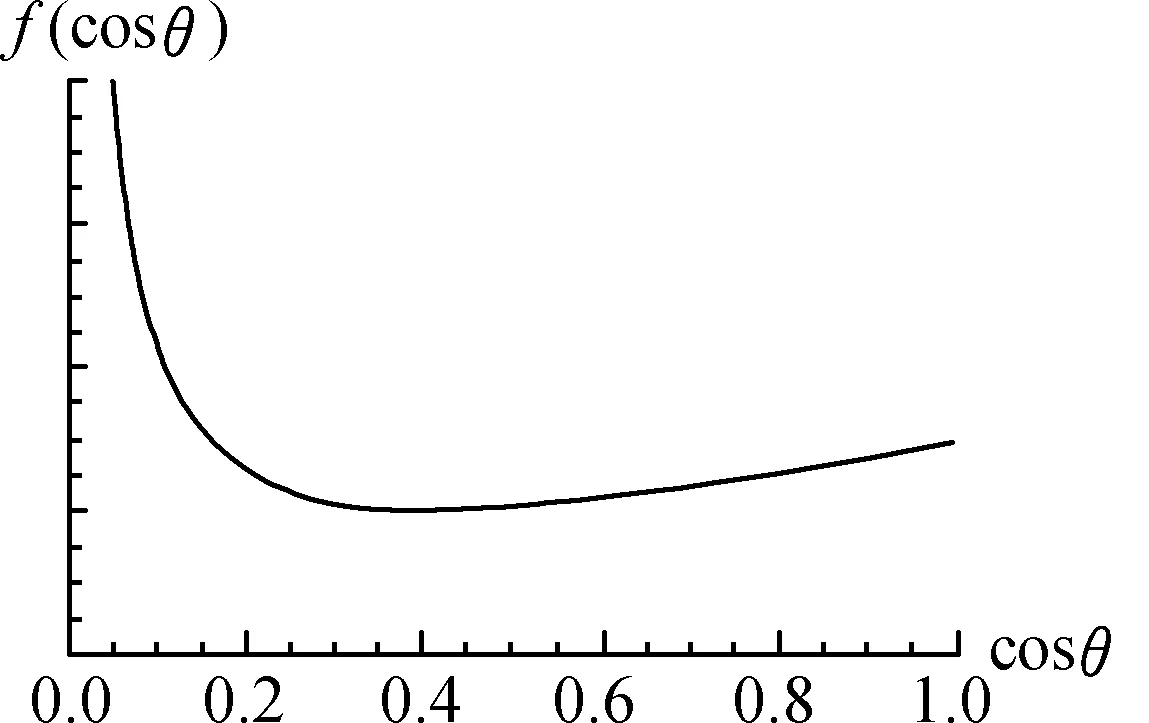
图3 f(cosθ)随cosθ的变化

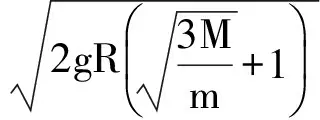
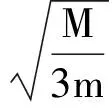
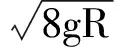
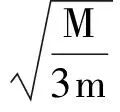
Mg+5mg.

对应的最低点速度满足

可得

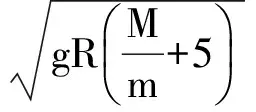
综上可得如下结论:

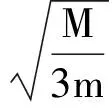
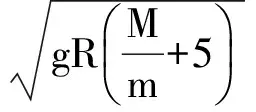
3 总结

经过分析发现此题不只是选择一个最高点模型,还要选择把轨道给顶起来的另一个模型,这个模型需要考虑到轨道质量和小球质量的关系．真正的解题需要将这两个模型相结合才可以．

数学是物理研究的工具和手段．对于物理问题的解决不是生搬硬套物理模型,还需用数学方法讨论．

1 陈汝冰，陈琳.浅析竖直平面内的圆周运动[J].物理教师，2015(3)：83-86.

2017-01-21)