复合土钉支护转角有利影响范围
2017-06-26张宗领王士革刘林超
张宗领+王士革+刘林超

摘要:基坑复合土钉墙转角处有明显的空间效应,受力变形较小,对支护结构有利,但不清楚转角定量的有利影响范围,目前设计中仍按照与基坑中部一样保守设计,为在此范围内降低土钉用量,避免保守设计,对水泥土搅拌桩复合土钉支护结构建立了全尺寸整体三维有限元模型,这种模型包含基坑的转角,能考虑基坑的空间效应,通过建立接触面单元,能考虑土体和搅拌桩、土体和土钉的相互作用,量化分析了基坑转角对支护结构受力和变形的有利影响范围,计算结果表明,基坑转角对开挖面水平位移、地表沉降、坑底隆起、土钉轴力的有利影响范围分别约为1.3、1、1、1.2倍的开挖深度。经与实际工程现场实测值对比,验证了该模型分析结果的可靠性,同时分析结果优于平面二维和局部三维有限元模型,结论为复合土钉支护结构的优化设计和安全施工提供了理论依据和研究方法。
关键词:复合土钉支护;基坑转角;有利影响范围;量化分析;有限元分析
中图分类号:TU476文献标志码:A文章编号:16744764(2017)03010708
Abstract:Foundation pit corner of composite soil nailed wall has obvious spatial effect. Supporting structure near foundation pit corner is safer due to smaller stress and deformation, Whilst at present quantitative beneficial affected area of foundation pit corner to the supporting structure are not known and designs are the same in the middle and the corner of foundation pit. In order to reduce the material consumption and avoid overcautious design, the construction process of excavation and supporting of the composite soil nailed wall of soil nailing and cementsoil piles for deep foundation excavation was simulated through establishing a whole threedimensional finite element model,which includes the corner of the foundation pit and can consider spatial effect of corner location and the interaction between soil nailing,cementsoil piles and soil through establishing interface elements. Beneficial affected area of foundation pit corner to stress and deformation of the supporting structure is analyzed and quantified. The calculation results show that beneficial affected area of foundation pit corner to the horizontal displacement of excavation face, the subsidence displacement of the ground beside the foundation pit,the bottom heave displacement and the axial forces of soil nails are about 1.3 times, 1 times, 1 times, 1.2 times of the excavation depth. Whole threedimensional finite element calculation results are basically consistent with those of the field test data and are more reliable than twodimensional or local threedimensional. These conclusions can provide theory basis and research method for optimization design and safety construction of composite soil nailed wall.
Keywords:composite soil nailed wall;foundation pit corner;beneficial affected area;quantitative analysis; finite element analysis
在有一定自立能力和較大摩阻力的土层中土钉支护得到了广泛应用,但在一些不良土层(如软土、松散砂土)中或对变形有严格要求的情况下,纯土钉支护难以凑效,近年来又发展了土钉和水泥搅拌桩、超前微桩、锚杆等组成的复合土钉支护[14]。其中以土钉+水泥土搅拌桩复合土钉最具代表性。
由于有限元程序在基坑工程设计和分析中提供的信息量非常丰富。近年来,很多学者采用有限元法对复合土钉支护进行了研究,得到了一些有益的成果。刘日成等[3]、俞缙等[5]分别对土钉+水泥土搅拌桩、土钉+锚索复合土钉墙建立了二维有限元模型,分析了支护结构的受力和变形。李彦初等[6]对土钉+锚索、土钉+钢管桩复合土钉支护结构建立了局部三维有限元模型,分析了土钉的轴力和开挖面的水平位移。潘泓等[7]建立了土钉+水泥土搅拌桩复合土钉墙的整体三维有限元模型,定性分析了转角对支护结构变形的影响。
复合土钉局部三维有限元模型和整体三维有限模型从模型尺寸上讲都是三维有限元模型,但局部三维模型沿坑壁的计算尺寸取的是一倍的土钉水平间距,且一般取偏离转角处的基坑中部,不能分析基坑转角处的受力和变形,而整体三维模型的计算尺寸取的是整个基坑大小(若基坑双向对称,可取四分之一),且包含基坑的转角,能更好的考虑基坑的空间效应,可全面分析基坑各处的受力和变形。
从以上可知,采用有限元法研究,前人对复合土钉墙建立的二维或局部三维模型均不包含基坑转角,不能考虑基坑转角处的空间效应[89],更不能定量分析转角的有利影响范围,前人建立的整体三维有限元模型仅定性分析了转角对支护结构变形的影响,没有分析对受力的影响,也没有定量分析转角的有利影响范围。针对这些问题,本文利用有限元软件ADINA,基于工程实例,对土钉+水泥土搅拌桩复合土钉墙建立了全尺寸整体三维有限元计算模型,模拟了开挖和支护的施工过程,量化分析了基坑转角对支护结构受力和变形的有利影响范围,以期为复合土钉墙的优化设计和安全施工提供参考。
1工程概况和支护方案
西安高新区某商住楼工程,地下2层,地上15层,建筑场地东西长约70 m,南北宽约40 m,基础类型为承台下钻孔灌注桩。基坑开挖深度为自然地面下8.2 m,地质条件:1)素填土:层厚1.30~350 m。2)黄土:可塑,很湿~饱和,中压缩性土,层厚0.30~1.60 m。3)黄土:软塑~流塑,饱和,高压缩性土,层厚1.30~2.50 m。4)黄土:软塑,局部为流塑,饱和,中偏高压缩性土,层厚6.10~6.80 m。5)古土壤:可塑~软塑,中压缩性土,层厚3.30~520 m。6)粉质粘土:硬塑~可塑,中偏低压缩性上,层厚20 m。地下水埋深3~4 m,属潜水。
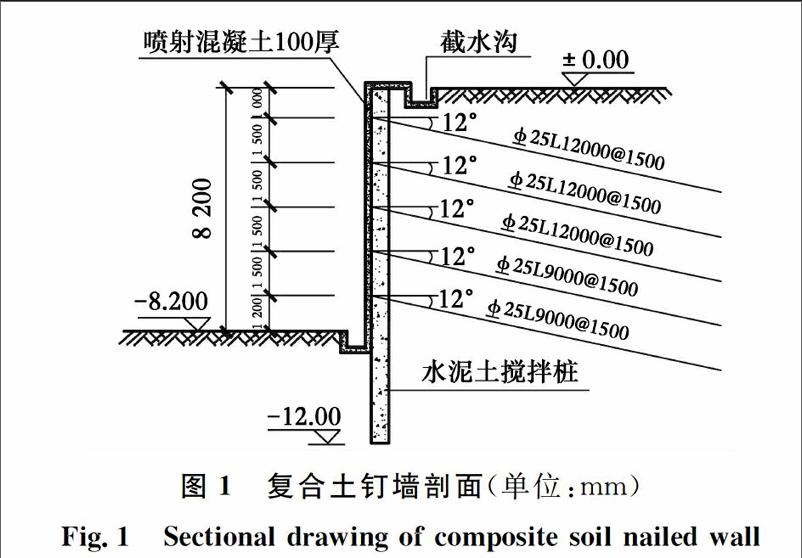
根据现场环境、开挖深度和水文地质条件,结合以往该地区基坑围护经验,对基坑的东侧和北侧采用了土钉+水泥土搅拌桩复合土钉支护,垂直开挖,采用单排直径0.65 m搅拌桩作为超前支护,桩间搭接0.15 m,桩长12 m,共设置五排土钉,从上往下土钉长度分别为12、12、12、9、9 m,土钉水平和竖向间距均为1.5 m,土钉倾角均为12°。采用钻孔注浆式土钉,钻孔直径为100 mm,土钉钢筋采用直径为25 mm的HRB335螺纹钢筋,基坑侧壁挂网喷射100厚混凝土面层,复合土钉支护剖面如图1所示。
2整体三维有限元模型的建立
2.1计算域、边界条件
为了节约计算时间,同时又能考虑基坑的整体空间作用,根据基坑的对称性,仅取包含轉角的基坑的1/4(35 m×20 m)进行分析,模型仍属整体三维有限元模型。根据前人的分析结果[10],基坑开挖影响宽度约为开挖深度的3~4倍,影响深度约为开挖深度的2~4倍。取整体三维有限元的尺寸为64 m×49 m×33 m,相当于向基坑X、Y(宽度)方向扩展了3.5倍的开挖深度,向基坑Z(深度)方向扩展了3倍的开挖深度。边界条件:底部为固定边界,侧面为滑移边界,顶面为自由边界。
2.2模型参数
在有限元分析中,考虑到软土的特性及复合土钉墙的工作性状,参考目前国内外同类研究方法[1114],土体采用摩尔库伦模型,即按弹性理想塑性材料考虑,屈服面为多边形,尽管不能考虑材料的硬化特征,但由于其参数简单,容易获得,目前在有限元分析中还是应用最为广泛的土体本构模型,根据工程地质勘察报告计算模型取用的土层计算参数见表1。分析中对桩模型作了一定的简化,用厚度0.6 mm的水泥土连续墙代替水泥土搅拌桩,钢筋混凝土面层和水泥土连续墙均按线弹性材料考虑,其计算参数见表2。土钉采用rebar杆单元,按线弹性材料考虑,其弹性模量按钢筋考虑,其计算参数见表3。
2.3土体和搅拌桩、土体和土钉的相互作用
由于搅拌桩和土体刚度相差较大,在开挖过程中,会产生相对滑动、脱离,甚至出现裂缝,土体和土钉之间也会产生滑移,整体三维模型利用ADINA软件提供的接触面单元,考虑土体和土钉以及土体和搅拌桩的相互作用。接触面单元为无厚度接触摩擦型单元,通过在接触面上同一位置处设置编号不同的两个节点,每对节点之间采用具有切向和法向刚度的“弹簧”相连接,使该单元承受切线方向的剪应力与法线方向的法向应力。接触面单元的切向刚度取为100 kN/m3,法向刚度取为4×104 kN/m3。
2.4开挖、支护施工过程的模拟
基坑的开挖和支护,涉及结构材料的减少或增加,可利用ADINA软件提供的“生”(单元刚度为1)、“死”(单元刚度为0)功能实现,且刚度可在1~0之间线性变化,ADINA的单元“死亡”功能对单元(材料)刚度的处理与其它软件不同,其刚度的变化不是瞬间完成,而是在用户指定的一个时间段从真实刚度降低到零,这更加符合工程实际。
除水泥土搅拌桩是预先施工外,基坑开挖与土钉支护都分步完成,共分5步,第1步开挖2 m,第2、3、4、5步挖深分别为1.5、1.5、1.5、1.7 m。每步开挖后,钻孔,置入土钉,注浆,挂网,喷射混凝土面层。有限元模拟的开挖步数、每步开挖的深度均与实际施工过程相一致。
最终建立的开挖前的整体三维有限元模型如图2所示,土钉+水泥土搅拌桩分布形式如图3所示。
3有限元模拟结果及分析
3.1转角对开挖面水平位移影响范围分析
图4为最后一步支护完成后基坑北侧开挖面水平位移云图。图5为最后一步支护完成后距基坑转角距离分别为1、3、5、7、9、11、13 m处开挖面水平位移随深度变化曲线。从以上两图可以看出:
上部水平位移小,中下部水平位移大,呈“鼓肚”形分布,这与许多学者的结论是一致的[1516]。最大水平位移约为0.5%倍的开挖深度,与文献[17]中结论一致。
2)基坑转角处的开挖面水平位移很小,随着距转角距离的增加水平位移逐渐增大,到达一定距离后水平位移增加缓慢直至不增加,分析其原因,是由于转角处两个方向的开挖面互为支撑,这种支撑作用使转角处的土体更稳定,有效的约束了转角处的开挖面水平位移,到达一定距离后这种支撑作用减弱直至消失。
3)距转角距离超过11 m后,开挖面水平位移曲线基本重合,说明转角的支撑作用基本消失,因此,此距离为转角对水平位移的有利影响范围。
4)随着距转角距离的增大水平位移的增大是呈非线性的,分析其原因,这与土体的非均匀性有关,各种不同物理参数和力学特性的土层组合成的土体造成了这种非线性。
图6为最后一步支护完成后开挖面中下部(距地表6.5 m处)从基坑转角到远离转角的开挖面水平位移变化图。开挖面水平位移随距基坑转角距离的增加而增加,大约在距转角11 m(约1.3倍的挖深)处达到与中部相同,结论与图5一致,也即基坑的转角效应对开挖面水平位移的影响范围约为1.3倍的开挖深度。
在基坑转角影响范围内,可通过增大土钉间距或减小钢筋直径或减小钢筋长度等措施来降低土钉用量,避免保守设计,以达到节约工程成本的目的。
3.2转角对坑后地表沉降影响范围分析
图7为最后一步支护完成后地表沉降云图,图8为不同开挖阶段地表沉降曲线,从图可以看出:
各个开挖阶段的地表沉降曲线均呈勺子形状,最大沉降值出现在距开挖面7 m左右,约为开挖深度的0.85倍。随着开挖的进行,最大沉降点略向坑边前移,这可能由于下部土体较软的原因。最大沉降位置随挖深增加向坑边的前移,也导致了开挖面中下部水平位移较大。
2)基坑转角附近的地表沉降明显小于远离转角处的地表沉降,分析其原因,是由于转角处两个方向的开挖面互为支撑,这种支撑作用有效的约束了地表沉降。
图9为最后一步支护完成后基坑东侧距开挖面6 m处(即最大沉降处)从基坑转角到基坑中部的地表沉降变化图。由图可以看出,地表沉降随距基坑转角距离的增加而增加,大约在距转角8 m(约1倍的挖深)处达到与中部相同,也即基坑的转角效应对地表沉降的影响范围约为1倍的开挖深度。
3.3转角对坑底隆起影响范围分析
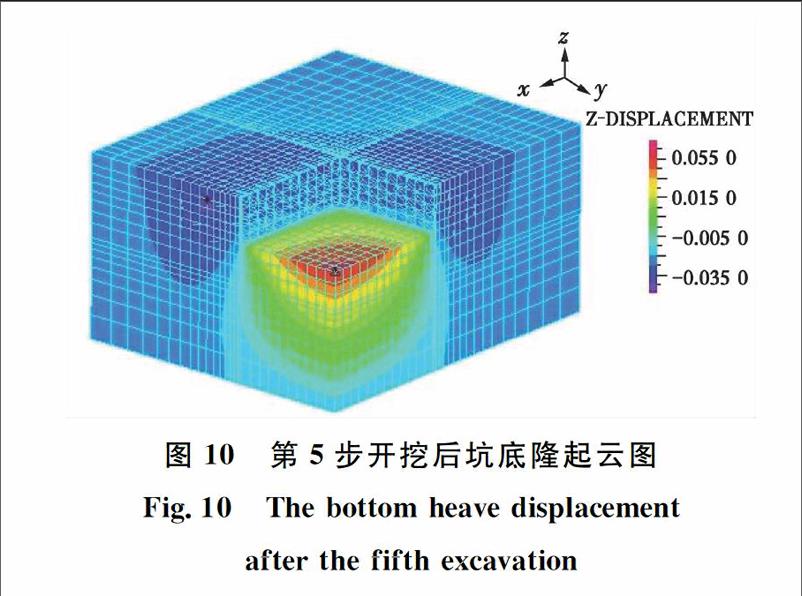
图10为最后一步支护完成后坑底隆起云图,从图10可以看出:基坑转角附近的坑底隆起明显小于别处,分析其原因,是由于转角处两个方向的开挖面互为支撑作用,这种支撑有效的约束了坑底隆起。
图11为不同开挖阶段非转角处坑底隆起曲线,从图11可以看出,非转角处的开挖面底部对坑底隆起的影响范围约为6.5 m(约0.7倍的挖深)。
图12为最后一步支护完成后从基坑转角到基坑中心的坑底隆起变化图。从图12可以看出,坑底隆起随距基坑转角距离的增加而增加,大约在距转角8 m(约1倍的挖深)处达到与中部相同,也即基坑的转角效应对坑底隆起的影响范围约为1倍的开挖深度。
3.4基坑转角对土钉轴力影响范围分析
图13、14为最后一步支护完成后各排土钉轴力图,可看出:
1)中下部土钉轴力较大,这与开挖面中下部水平位移较大的分布规律基本一致。
2)基坑转角处的各排土钉轴力明显小于远离转角处的土钉轴力,分析其原因,是由于转角处两个方向的开挖面互为支撑作用,这种支撑约束了开挖面的水平位移,保护了土体的稳定性,也使土钉轴力变小了。
图15为最后一步支护完成后从基坑转角到远离基坑转角方向各排土钉轴力的变化图。由图可以看出,各排土钉轴力随距基坑转角距离的增加而增加,大约在距转角9.5 m(约1.2倍的挖深)处达到与中部相同,也即基坑的转角效应对土钉轴力的影响范围约为1.2倍的开挖深度。
3.5现场实测验证
为了验证整体三维有限元模拟结果的可靠性和精度,除了实测值验证外,本文还建立了局部三维有限元模型和二维有限元模型和其进行对比。图16、17分别为基坑北侧某水平位移观测点和基坑东侧某地表沉降观测点在每步开挖支护完成后的实测值与模拟分析值的对比图,模拟值包括整体三维有限元模型模拟值、局部三维有限元模型模拟值、二维有限元模型模拟值。
1水平位移观测点和沉降观测点是在开挖支护前布的点,实测值测的是从开挖到支护完成后的位移,模拟值提取的也是从开挖到支护完成后的位移,模拟值和实测值理论上应该相等,但由于输入的土体等材料参数和实际的偏差,测点的具体位置与模拟中的精确位置的偏差,以及模型的抽象简化,这些因素都会使模拟值和实测值有一定差别。
从图16和图17中可以看出,整体三维有限元模型模拟值无论在数值上还是在形态上均接近实测值,且计算结果的精度优于局部三维和二维有限元模型,说明建立的搅拌桩+土钉复合土钉支护整体三维有限元计算模型是符合工程实际的,计算结果是可靠的,可以运用于实际工程的分析和预测。
4结论
通过对西北黄土地区基坑土钉+水泥土搅拌桩复合土钉支护进行整体三維有限元分析,主要得到以下结论:
1)模型不仅能考虑基坑的空间效应,而且能考虑桩土、钉土间的相互作用,经与实测值比较,分析结果可靠,且优于局部三维和二维有限元模型。
2)基坑转角处两个方向开挖面后的搅拌桩和土体互为支撑,这种支撑作用有效的约束了支护结构转角处的受力和变形,使转角处更稳定、更安全。
3)量化分析了基坑转角对支护结构受力和变形的有利影响范围。基坑转角对开挖面水平位移的影响范围约为1.3倍的开挖深度,对地表沉降的影响范围约为1倍的开挖深度,对坑底隆起的影响范围约为1倍的开挖深度,对土钉轴力的影响范围约为1.2倍的开挖深度。
4)在转角影响范围内,可根据影响的大小以及距基坑转角的远近适当减少土钉的用量以降低工程造价。
5)所分析的基坑转角为阴角,至于基坑阳角的空间效应需要进一步研究。
6)由于岩土有地域性特点,随着土体物理和力学参数的变化,本文得到的一些定量结论也会发生一些变化,这需要继续研究。
参考文献:
[1] 付文光, 杨志银, 刘俊岩, 等. 复合土钉墙的若干理论问题、兼论《复合土钉墙基坑支护技术规范》[J]. 岩石力学与工程学报, 2012,31(11): 22912304.
FU W G, YANG Z Y, LIU J Y , et al. Some theoretical questions of composite soil nailing wall and discussion on Technical Code for Composite Soil Nailing Wall in Retaining and Protection of Excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2012,31(11): 22912304.(in Chinese)
[2] FU W G. The application of composite soil nailing wall in China[J]. Japanese Geotechnical Society Special Publication, 2016, 2 (64): 21922195.
[3] 劉日成, 张芹, 王育奎. 复合土钉墙支护效果数值模拟[J]. 地下空间与工程学报, 2012, 8(1): 182188.
LIU R C,ZHANG Q, WANG Y K, et al. Numerical simulation of composite soil nailed wall[J]. Chinese Journal of Underground Space and Engineering. 2012,8(1): 182188.(in Chinese)
[4] 付文光, 杨志银. 复合土钉墙整体稳定性验算公式研究[J]. 岩土工程学报, 2012,34(4): 742747.
FU W G, YANG Z Y. Formulae for overall stability of composite soil nailing walls[J]. Chinese Journal of Geotechnical Engineering, 2012,34(4): 742747.(in Chinese)
[5] 俞缙, 王艳芳, 宋博学. 复合土钉支护的软土基坑开挖有限元模拟分析[J]. 华侨大学学报(自然科学版), 2011, 32(2): 212217.
YU J, WANG Y F, SONG B X. FEM simulation of composite soil nailing supported excavation in soft clay pit[J]. Journal of Huaqiao University (Natural Science), 2011,32(2): 212217.(in Chinese)
[6] 李彦初, 陈轮. 深基坑复合土钉支护的三维有限元数值分析[J]. 工程勘察, 2012 (2): 1115,32.
LI Y C, CHEN L. 3D numerical analysis on composite soil nailed structure for deep excavation with FEM [J]. Geotechnical Investigation & Surveying, 2012(2): 1115,32.(in Chinese)
[7] 潘泓, 周陈发, 曹洪. 复合土钉墙的角部空间效应及变形性状分析[J]. 岩土力学, 2008,29(2): 333336.
PAN H, ZHOU C F, CAO H. Analysis of spatial effectand deformation of corner of composite soil nailing walls [J]. Rock and Soil Mechanics, 2008, 29(2): 333336.(in Chinese)
[8] OU CU, CHIOU D C, WU T S. Threedimensional finite element analysis of deep excavations[J]. Geotechnical Engineering, ASCE, 1996, 122(5): 337345.
[9] SMITH I M. Threedimensional FE analysis of a nailed soil wall curved in plan[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1997, 21(9): 583597.
[10] 张宗领, 张昊, 付超, 等. 钉距和微预应力对复合土钉墙性能影响的有限元分析[J]. 信阳师范学院学报(自然科学版), 2012, 25(3): 416420.
ZHANG Z L, ZHANG H, FU C, et al. Finite element analysis of the influence of the distance of nails and small prestress on behavior of composite soil nailed wall[J]. Journal of Xinyang Normal University(Natural Science Edition), 2012,25(3): 416420.(in Chinese)
[11] 徐帮树, 刘日成, 李连祥, 等. 复合土钉墙支护设计参数敏感性分析及边坡变形规律研究[J]. 岩土力学, 2011, 32(2): 393400.
XU B S, LIU R C, LI L X, et al. Study of slope deformation and parameters sensitivity in supporting design of composite soil nailing wall [J]. Rock and Soil Mechanics, 2011,32(2): 393400.(in Chinese)
[12] SMITH I M. Threedimensional analysis of reinforced and nailed soil[C]//Proceedings of the International Symposium on Numerical Models in Geomechanics. Rotterdam: Balkema A A, 1992: 829838.
[13] HO D K H, SMITH I M. Modelling of soil nailing construction by 3dimensional finite element analysis[C]//Proceedings of Conference on Retaining Structures, Cambridge: [s. n.], 1992: 515528.
[14] TABRIZI S K. 3D finite element modeling of soilnailed wall [D]. New Jesey: The State University of New Jesey, 1996: 550563
[15] 李连祥, 王春华, 周婷婷, 等. 微型桩与帷幕的不同位置对复合土钉墙力学性状的影响分析[J]. 岩土力学, 2015,36(Sup1):501505.
LI L X, WANG C H, ZHOU T T, et al. Impact of position of micro pile on mechanical behaviors of composite soil nailing wall curtain [J]. Rock and Soil Mechanics, 2015,36(Sup1): 501505.(in Chinese)
[16] 周健, 李飞, 张姣, 等. 复合土钉墙支护基坑颗粒流数值模拟研究[J]. 同济大学学报(自然科学版), 2011, 39(7): 966971.
ZHOU J, LI F, ZHANG J, et al. Study of PFC numerical simulation of soil nailing wall support excavation [J]. Journal of Tongji University(Natural Science), 2011, 39(7): 966971.(in Chinese)
[17] 杨育文. 复合土钉墙实例分析和变形评估[J]. 岩土工程学报, 2012,34(4): 734741.
YANG Y W. Case studies of composite soilnailing walls and movement estimate [J]. Chinese Journal of Geotechnical Engineering, 2012,34(4): 734741.(in Chinese)
(編辑胡玲)
