地震作用下框架整体与局部损伤的相关性

刘哲锋+陈逵+赵鹏+陈蔚

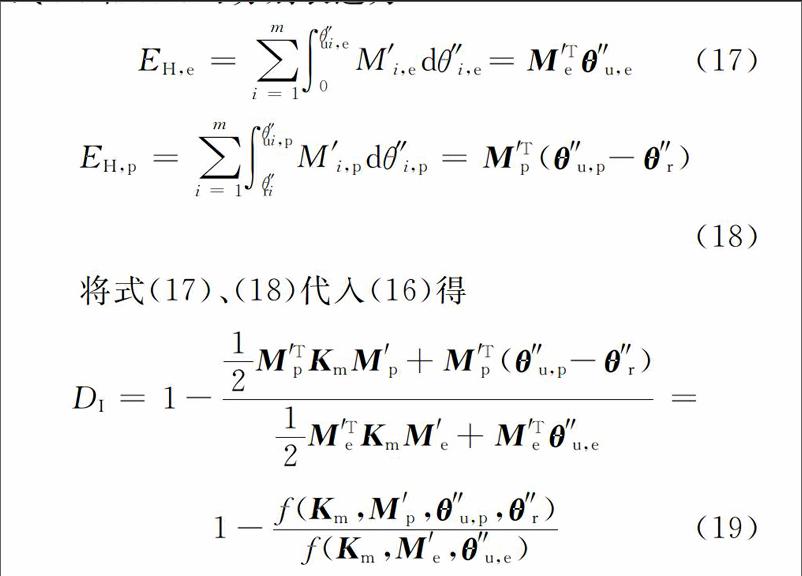
摘要：根据框架结构耗散塑性变形能与存储弹性变形能能力的损失界定结构的整体损伤，根据塑性铰耗散塑性变形能能力的损失来界定局部损伤，并以拟力法为基础推导了局部损伤与整体损伤的解析表达式，进而讨论框架结构局部损伤与整体损伤的相关性。研究表明，控制框架结构整体损伤的手段有：减小局部损伤区域的强度衰减、提高局部损伤区域的极限转动能力和减小局部损伤区域的残余变形。其机理是通过提高局部损伤区域的耗能能力与约束能力来提高整个结构耗散与存储地震能量的能力；框架结构整体损伤与局部损伤的加权值较为接近，可以采用框架局部损伤的加权值来近似估计结构的整体损伤值。

关键词：框架结构；拟力法；地震能量；整体损伤；局部损伤

中图分类号：TU375.4文献标志码：A文章编号：16744764（2017）03009207

Abstract：The global damage index of frame is defined as the loss of the strain energy dissipation capability during the pushover process， and the local damage index of plastic hinge is defined as the loss of hysteretic energy dissipation capability during the pushover process. Based on the force analogy method， the analytical expressions of the global local damage index are proposed. Besides， the correlation between global damage index and local damage indexes are discussed. The results show that improving hysteretic energy dissipation capability and constraint capacity to elastic portion of plastic hinges will effectively improve the strain energy dissipation capability of frame. There are three specific ways： reducing strength degradation， residual deformation and improving rotation capacity of plastic hinges. The global damage index is generally closed to weighted value of local damage indexes which taking the ratio of hysteretic energy dissipated by plastic hinge to total value dissipated by frame as weight. Therefore， the weighted value of local damage indexes could be used to estimate the global damage index of structure.

Keywords：frame work； force analogy method； seismic energy； global damage； local damage

在基于性能的抗震設计中，性态目标的确定是设计工作的基础，而对结构提出一个损伤量化指标是界定性态目标的前提。结构的地震损伤可以从整体和局部两个方面描述，前者获得结构损伤的整体信息，后者则获得结构损伤的分布信息。结构的整体损伤状态从根本上讲是各构件的局部损伤状态决定的，因此，一个合理的损伤指标应能描述结构的整体损伤状态与局部损伤分布，并揭示两者的机理相关性与量值相关性[12]。

目前已有的结构损伤评价模型大致可归纳为显式双参数和隐式双参数模型两类[3]。显式双参数模型在损伤表达式中直接包含了最大变形与累积滞回耗能（累积塑性变形能）参数项。如Park等[4]提出的两参数项线性组合的损伤模型及以此为基础的改进模型[57]。该类模型的建立以构件的实验结果为基础，在描述结构局部损伤时优势明显，但在计算结构整体损伤时需要引入构件重要性系数来对局部损伤进行加权组合，且加权方法基于研究者经验选取，理论上没有严格标准。隐式双参数模型直接利用地震前后结构特性（如刚度[810]、弹性应变能[11]、周期[12]等）的变化来描述结构的残余承载能力，并以此衡量结构的损伤。该类模型的优点在于能直接得到结构的整体损伤指标，不存在显式模式中的损伤组合问题，不足之处在于该类方法无法提供损伤的分布信息。

笔者基于隐式双参数模型模式，利用结构在单向振动过程中耗散塑性变形能与存储弹性变形能能力的变化来界定结构的损伤量值，并以拟力法为理论基础推导框架结构局部损伤与整体损伤的量值表达式，进而讨论结构整体损伤与局部损伤之间的机理联系与量值联系。

1基于拟力法的损伤分析

1.1拟力法

1999年Wong等[1314]提出拟力法，并将其应用于框架结构的动力弹塑性时程分析与能量反应分析中，其方法简要介绍如下。

假定框架在水平荷载作用下的塑性侧移由塑性铰的塑性转动引起。在框架每层定义一个水平位移自由度（共n个），在可能出现塑性铰的位置定义塑性转角自由度（共m个）。水平荷载F使框架发生屈服形成若干塑性铰，结构被分离为弹性状态与塑性状态的叠加。弹性状态框架承担外力F，发生弹性侧移X′，m个塑性转角自由度处的弯矩为M′（以下称弹性弯矩）；塑性状态框架的m个塑性转角自由度上的塑性转角为θ″，导致产生的塑性侧移为X″，由于各塑性转角自由度上的塑性转角不一定协调，因此m个塑性转角自由度上作用有弯矩M″（以下称塑性弯矩）。M′、M″、θ″为m阶列向量，F、X′、X″为n阶列向量。图1以单层框架为例说明了拟力法中框架受力状态的分解。

对于一个特定的框架，式（19）中的分母项是一定的，那么DI值主要受分子项影响，而分子项中的Km是一个与结构弹塑性状态无关的常量，因此，影响DI值的主要变量是M′p、θ″pu、θ″r。这3个变量均为塑性转角自由度的状态变量，即局部损伤的状态变量。M′p越大，DI值越小，即结构在地震的往复作用后，塑性转角自由度上的强度衰减越小，结构整体损伤越小；θ″pu越大，DI值越小，即塑性转角自由度上的极限转动量越大，结构整体损伤越小；θ″r越小，DI值越小，即地震后塑性转角自由度上的残余转角越小，结构整体损伤越小。

因此，对于框架结构的整体损伤，第一个控制手段是减小局部損伤区域的强度衰减，其机理是通过控制局部损伤区域的转动强度，一方面确保结构具备足够的耗散塑性变形能的能力，另一方面确保结构弹性部分受到足够的端部约束，从而保证结构存储弹性变形能的能力；后两个控制手段则分别是提高局部损伤区域的极限转动能力和减小局部损伤区域的残余变形，其控制机理都是通过增加局部损伤区域的转动行程来确保该区域的塑性耗能能力，从而保证结构耗散塑性变形能的能力。

1.3.2量值相关性以震前结构在单向受荷过程中塑性转角自由度上耗散的塑性变形能占总塑性变形能的比例为权数对结构的局部损伤进行加权，获得局部损伤的加权值dAdA=m1i=1EHi，e1EH，e·di=1-EH，p1EH，e（20）定义两个参数ξe=ES，e1EH，e，ξp=ES，p1EH，p（21）ξe和ξp分别为震前和震后结构在单向受荷过程中存储弹性变形能与耗散塑性变形能的比值。将式（21）代入式（4）并与式（20）联立，得DI=1-1+ξp11+ξe·（1-dA）（22）根据图3所示的简化关系，结构在单向荷载作用下达到极限位移时，存储的弹性变形能与耗散的塑性变形能的比例为ξ=112（μ-1）（23）式中：μ=uu1uy，是结构的位移延性系数。

图3单向荷载作用下结构吸收的能量

Fig.3Energy absorption by structure under single loading1结构的典型位移延性通常为3～5[17]，因此，ξ的取值范围为0.125～0.25。将ξp和ξe取值为0.1～03，代入式（22）讨论框架结构整体损伤与局部损伤加权值的关系，计算结果示于图4。由图可知，随着ξp和ξe的取值在0.1～0.3之间变化，DI与dA的关

图4局部损伤加权值与整体损伤的关系

Fig.4The relationship between weighted

value of local damage and global damage1系位于DI=dA两侧的狭长扇形区域内，这表明框架的整体损伤与局部损伤的加权值是接近的，且损伤越为严重，两者量值越为接近。当ξe=ξp时，DI=dA；当ξe>ξp时，DI>dA；当ξe<ξp时，DI

2算例

某3跨RC框架，底层高5 m，其余层高4 m，每跨跨度6 m（见图5）。梁200 mm×400 mm，柱450 mm×450 mm，采用C30混凝土，纵筋采用 HRB335，箍筋为HPB235，结构各层重力荷载代表值676 kN。分别取3层、6层和9层结构作为分析对象，结构自振周期分别为1.04、2.03、2.97 s。场地类别为II类，设防烈度7度，通过Midas Building进行配筋设计。动力时程分析采用IDARC7.0，滞回模型选用Vertex oriented model，滞回模型刚度退化参数为8.0，强度退化参数为0.1，阻尼模型采用质量比例模型。地震波采用表1所示的6条地震波，为了考虑频谱特性的差异，地震波峰值速度与峰值加速度的比值在0.12～0.18之间，分析时地震波幅值调幅为0.3 g。结构的单向推覆过程通过施加地面单向加速度时程来实现，具体方法见文献[16]。

各算例的dA与DI结果列于表2，将这些dADI关系用空心圆点绘于图4中得图6，可见算例结果确实位于DI=dA两侧的狭长区域中，且与直线DI=dA较为接近。这说明框架局部损伤的加权值可以用来对结构的整体损伤作近似估计。

图7列举了3个框架在3号地震波作用下的局部损伤分布图。可见，3层框架的局部损伤较为均匀，但对于6层和9层框架，尽管整体损伤指数分别只有0.15和0.22，但结构很多局部区域的损伤却远远高于该值。因此，对结构进行地震损伤评价时，除了对结构整体损伤进行量化评价外，更为重要的是了解构件的局部损伤和损伤在结构内部的分布情况。

13结论

1）由结构耗储能量能力的损失定义整体损伤，由构件端部耗散能量能力的损失定义局部损伤，并通过拟力法推导了框架结构局部损伤与整体损伤值的解析求解式。

2）控制框架结构整体损伤的手段为：减小局部损伤区域的强度衰减、提高局部损伤区域的极限转动能力、减小局部损伤区域的残余变形。其机理是通过提高局部损伤区域的耗能能力与约束能力来提高结构耗散与存储地震能量的能力。

3）建立了整体损伤DI与局部损伤加权值dA间的量值解析关系。DI与dA的数值位于DI=dA两侧的狭长区域内，可以采用框架局部损伤的加权值来近似估计结构的整体损伤。同时，受限于分析样本的数量，该结论的可靠性与适用性仍有待进一步完善。

参考文献：

[1] 李刚，程耿东.基于性能的结构抗震设计——理论、方法与应用[M].北京：科学出版社，2004.

LI G， CHENG G D. The performance based seismic design：Theory， method and application [M]. Beijing： Science Press， 2004. （in Chinese）

[2] 吕西林，章红梅.对《建筑工程抗震性态设计通则（试用）》的评述 [J].地震工程与工程振动，2005，25（4）：180186.

LYU X L， ZHANG H M. Comments on “General rule for performance –based seismic design of buldings” [J]. Earthquake Engineering and Engineering Vibration， 2005， 25（4）： 180186. （in Chinese）

[3] 于琦，孟少平，吴京.基于变形与能量双重准则的钢筋混凝土结构地震损伤评估[J].土木工程学报，2011，44（5）：1623.

YU Q， MENG S P， WU J. Deformation and energybased seismic damage evaluation of reinforced concrete structures [J]. Journal of Civil Engineering， 2011， 44（5）： 1623. （in Chinese）

[4] PARK Y J， ANG A H S.Mechanistic seismic damage analysis of reinforced concrete [J]. Journal of Structural Engineering， ASCE， 1985， 111： 722739.

[5] KUNNATH S K， REINHORN A M， LOBO R F. IDARC Version 3.0： A program for the inelastic damage analysis of reinforced concrete structures： Report No. NCEER900022 [R]. National Center for Earthquake Engineering Research， State University of New York at Buffalo， 1992： 132151.

[6] 丁阳，伍敏，徐龙河，等.钢柱考虑损伤累积效应的强震下损伤演化规律[J].建筑结构学报，2011，32（7）：112117.

DING Y， WU M， XU L H， et al. Seismic damage evolution of steel columns considering damage accumulation [J]. Journal of Building Structures， 2011， 32（7）： 112117. （in Chinese）

[7] 尹犟，易偉建，胡其高.结构整体抗震性能评估新方法[J].工程力学，2010， 27（3）： 123131.

YIN J， YI W J， HU Q G. The new method for estimating seismic performance of structures [J]. Engineering Mechanics， 2010， 27（3）： 123131. （in Chinese）

[8] GHOBARAH A， ABOUELFATH H， BIDDAH A. Responsebased damage assessment of structures [J]. Earthquake Engineering and Structural Dynamics， 1999， 28： 79104.

[9] 阳洋，周锡元，金国芳，等.框架结构基于改进直接刚度法的地震损伤评估[J].振动与冲击，2011，30（2）：199204.

YANG Y， ZHOU X Y， JIN G F， et al. Modified direct stiffness calculation method for seismic damage assessment of frame structures [J]. Vibration and Shock， 2011， 30（2）： 199204. （in Chinese）

[10] 吴子燕，韩晖，刘书奎.基于刚度损伤指数的桥梁整体损伤程度模糊评定研究[J].工程力学，2011，28（12）：9297.

WU Z Y， HAN H， LIU S K. Research on fuzzy assessment on the degree of bridge damage using stiffness damage index [J]. Engineering Mechanics， 2011， 28（12）： 9297. （in Chinese）

[11] ROBERTO S， LEOPOLDO T， RENATO V， et al. Global damage indexes for the seismic performance assessment of RC structures [J]. Earthquake Engineering and Structural Dynamics， 2009， 38： 10271049.

[12] ALI M， EHSAN M. A new damage index for RC buildings based on variations of nonlinear fundamental period [J]. The Structural Design of Tall and Special Buildings， 2013， 22（1）： 5061.

[13] WONG K K F， YANG R. Inelastic dynamic response of structures using force analogy method [J]. Journal of Engineering Mechanics， ASCE， 1999， 125（10）： 11901199.

[14] KEVIN K F， WONG R Y. Earthquake Response and Energy Evaluation of Inelastic Structures [J]. Journal of Engineering Mechanics， ASCE， 2002， 128（3）： 308317.

[15] 刘哲锋，沈蒲生.基于拟力法的地震能量反应分析[C]//防震减灾工程研究与进展—全国首届防震减灾工程学术研讨会论文集，2004： 184190.

LIU Z F， SHEN P S. Seismic energy response of structures using force analogy menthod [C]//Research and Development of Earthquake Prevention and Disaster Reduction Engineering： The First National Symposium on Earthquake Mitigation Set， 2004： 184190. （in Chinese）

[16] 刘哲锋，周琼，陈逵.基于能量耗储能力的结构损伤量化研究[J].工程力学，2013，30（2）：169173.

LIU Z F， ZHOU Q， CHEN K. Quantitative analysis of seismic damage based on structural energy dissipation and storage capability [J]. Engineering Mechanics， 2013， 30（2）： 169173. （in Chinese）

[17] PARK R， PAULEY T. 鋼筋混凝土结构[M]. 重庆：重庆大学出版社，1985.

PARK R， PAULEY T. Reinforced concrete structure [M]. Chongqing： Chongqing University Press， 1985. （in Chinese）

[18] 陈逵，刘哲锋，沈蒲生.延性系数对SDOF体系地震能量输入历程的影响研究[J].地震工程与工程振动，2010，30（6）：5664.

CHEN K， LIU Z F， SHEN P S. Study on the effect of ductility coefficient on input energy time histories for inelastic SDOF systems [J]. Earthquake Engineering and Engineering Vibration， 2010， 30（6）： 5664. （in Chinese）

（编辑胡英奎）