如何在时空下对点线面体作优化测算

广东惠州市大亚湾第一中学 李玉发

澳大利亚国立大学硕士研究生精算专业2017级) 李宇航

1. 基本原理

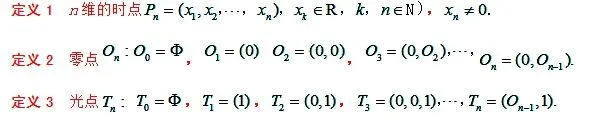
为了点的不同维度的点能加减，我们提出升维、加减的相关定义：

定义5是坐标原点 4)点量：

定义6 关于时空间有

（1）（称为零维点空间）；

（2）（称为n维时空间），从而有时点当是点（线、面、体）空间.

定义7 含有未知数的等式叫数方程，含有未知点的等式叫形方程。

2.（直线、平面、四面体的）形方程的一些主要结论

定义8（直线、平面、四面体的）形方程

①是T上的一个A点的方程. A的测度记为D0.

是线段A1A2的方程，P是线段A1A2的内点，线段A1A2的长度记为D1,线段P A2的长度记为M1,线段A1P的长度记为M2,则有

③A1,A2,A3三点不共线，则是三角形的面方程，P是的内点，的面积记为的面积记为M1，的面积记为M2，的面积记为M3，则有:

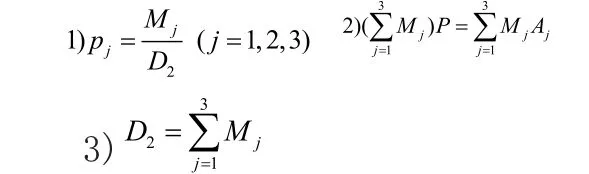
A1、A2、A3、A4四点不共面，则是环空间T4上四面体的方程，P是四面体的内点，四面体的体积记为四面体的体积记为四面体的体积记为四面体的体积记为四面体的体积记为M4,则有:

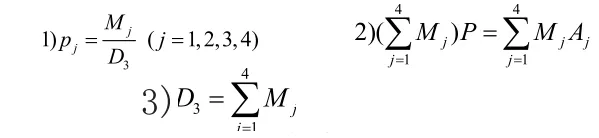
定义9. n维直形多面体

称是n维时空间Tn上直形多面体Xn的时空概率方程。P是多面体Xn的内点，A1A2...An的测度记为Dn−1，的测度记为的测度记为的测度记为MN，则对Xn的概率方程有以下重要结论（超概率杠杆原理）：

结论1：

结论2.

结论3.

3. 时空下的五观--时空观

1）升维降维—运动观

2）空间与形方程---形观

3）点量、线量、面量----数量观

4）曲直可统一、高低可统一、分支有共性---统一观

5）点难线易、线难面易、面难体易、静难动易、正难反易…转换观

4. 具体应用

4.1 点线转换、线面转换、面体转换

例1.已知A(2,5),B(-1,-1),直线AB与y轴交于

点P（0，t），,求（1）t的值，（2）求λ的值。

分析一:（点观法）：

设 直 线AB：，故有：

分析二:（线观法）：由超 概 率 杠 杆 原理结论2：

感悟：这个问题点观数法繁难，故线观形法一定简便. 方法：点难线易。

例2图1四棱锥P-ABCD中，面，则（1）AB-P-CD二面角大小的正切值是_____________

（2001年全国高考理科立体几何题）（2）点A到面PBD的距离

分析：（1）设二面角大小为θ，可证明则

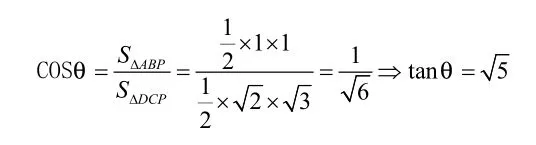
（2）由等体积法可得，

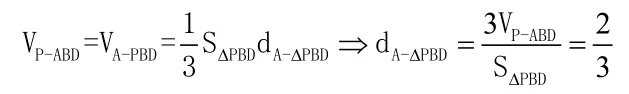
感悟：这个问题直接求繁难，转换后简便. 方法：线难面易、面难体易。

4.2 物理模型与概率杠杆模型的转换

例3 （2004年全国初中联赛CASIO杯武汉选拔赛试题）如图2，在中，D是AC的中点，E、F是BC的三等分点，AE、AF分别交BD于M、N两点，则有BM：MN：ND=（ ） A、3:2:1 B、4:2:1 C、5:2:1 D、5:3:2

分析：直接用相似三角形知识，要作辅助线运算量较大，考虑化归为物理问题。

解法一：[建物理模型]在图2中把杆杆AC、BC、AE对应的支点分别为D、E、M，则用杠杆原理悬挂法可解决。为此考虑图3和图4。在图2中，设BM=x、MN=y、ND=z.，由图3：BE：EC=1：2,D是中点, 以E点为支点，BC为杆杆有：

以D点为支点，AC为杆杆有：

以M点为支点，BD为杆杆有：

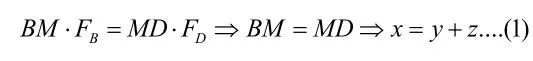
由图4：BF：FC=2：1,D是中点,同理可得：

以N点为支点，BD为杆杆有：

由（1）、（2）可得：，选D答案。

解法二：在图中, BE：EC=1：2、BF：FC=2：1,D是中点，由超概率杠杆原理结论2得：

由

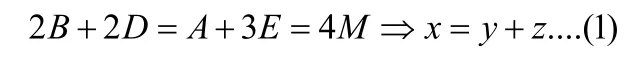
由

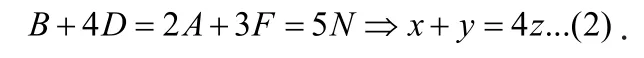
由（1）、（2）可得：选D答案。

感悟：解法二用了超概率杠杆原理，显然简单易行！方法：化归难升维易。

4.3 特殊与一般的转换（线面转换，面体转换）

例4.O是三角形面内部的任意一点，ABC∆的面积记为S，的面积记为的面积记为S2，ABO∆的面积记为S3，求证（奔弛定理）

解法一：过B点作BDOA⊥于D,过C点作CEOA⊥于E,设则与共线，则与在垂直于的反向上的投影长度相等，方向相反，则因为共线，所以同理可得所以得证.

解法二：由超概率杠杆原理结论2：得证.

感悟：解法一是把面化归为线问题是降维，解法二是在面内直接解决问题，形升数降，形降数升，所以解法二比解法一快捷了许多.方法：线难面易。

4.4 静与动的转换

例5求函数的值域.

感悟：t是x的一元函数，函数图形是静曲线，t转换为x与y的二元函数，定义域是二维的半圆C，函数图形是动直线l，t是直线l的斜率。方法：静曲线难动直线易。

4.5 高低转换

例6.求不等式的解集（2014年广东理科第9题）

分析：原不等式等价于不等式：其中这又等价于不等式组：

易解得：

感悟：把一元不等式转换为二元不等式组，比较难求一维的边界点升维转换为易求的椭圆边界曲线的顶点方法：点难线易、低难高易。

例7（2017全国I卷数学理科高考第20题） 已知椭圆的四点为恰有三点在椭圆C上。

（1）求椭圆C的标准方程；

（2）设直线L不经过P2点且与C想交于A、B两点，若直线怕P2A的斜率与直线P2B的斜率的和为-1，证明L过定点。

解：(1)由

（2）直线L与椭圆C分别交于，则设直线L的方程

构造下面方程组：

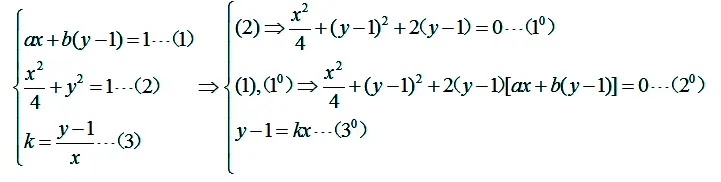
感悟：本题（2）有多种求法，可以从不同的角度去思考，可以用点差法、或弦长公式结合韦达定理去求点P的轨迹方程，但运算量较大，隐含线量的意义，点差法与弦长公式更多是点量的含义，由点量升维到线量，形升则数降，所以代数运算量就减少了！。方法：点难线易

总论：

一）方法：代数难题用几何法、几何难题用代数法、等式难题用不等法、不等难题用等式法、数形难题用升维法.总之数难形易、形难数易、点难线易、线难面易、面难体易、体难时易、正难反易、静难动易、实难虚易、低难高易、直难曲易、如此下去,天下无难!

二）感悟：化归是一种降维，化归的反面是升维，降维难算，升维易解。登高而望，跳出难题之外，不在常规之中，难题若是魔高一尺，升维就来道高一丈！天下无难题，只要肯升维！

[1]理论来源：1）李玉发、李宇航.时空Tn中点线面体的运算、变换、转换[J]华南师范大学学报（自然科学版）2014年第46卷129页-131页. 2）李宇航.数学中的运算、变换、转换[D].全国中学生数理化学科能力展示活动一等奖建模论文.2011年

[2]李玉发、李宇航.利用空间维度变换，速解高中数学难题[D].全国初等数学研究会和广东初等数学研究会联合颁发的二等奖论文,2017年1月3日

[3]李玉发.点线面体的五观报告.全国初等数学研究会第十届研讨会暨广东省初等数学学会一届三次学术研讨会.2017年1月3日

[4]李玉发.中学数学教育中的美育——浅谈数学教学中的美育渗透[D].广州：华南师范大学,2001

[5]李玉发.转换是数学中的美旋律[J].中学数学研究，2007,第4期第25页