导数在中学数学中的应用

辽宁省锦州市义县高级中学 高 微

例1 试求曲线

导数是高中数学新教材中新增内容之一，它的引入给传统的中学数学内容注入了新的生机和活力，也为中学数学解决问题注入了新的途径和方法。导数在解决函数单调性问题，求函数极值和最值，不等式证明以及解决解析几何中与切线有关的问题和最值问题有着广泛的应用。其方法较传统的方法简洁、灵活，而导数与函数、不等式、解析几何、数列、向量等知识结合起来，也使命题的设计更加广阔了。

一、在函数方面的应用

运用导数知识研究函数性质的试题，研究对象已经突破了单+纯的一次函数、二次函数、指数函数、对数函数等命题常以复合的函数形式出现。解决这一类型的题往往采用新旧结合以旧代新方法解决旧问题。

（一） 函数单调性的讨论

函数的单调性是函数最基本的性质之一，是研究函数所要掌握的最基本的知识。通常用定义来判断，但当函数表达式较复杂时判断正负较困难。运用导数知识来讨论函数单调性时，只需求出再考虑的正负即可。此方法简单快捷而且适用面广。

（二）函数的最值（极值）的求法

最值（极值）问题是高中数学的一个重点，也是一个难点.它涉及到了中学数学知识的各个方面，用导数解决这类问题可以使解题过程简化，步骤清晰，也好掌握。

一般地，函数f(x)闭区间[a，b]上可导，则f(x)在[a，b]上的最值求法 ：

①求函数f(x)在（a，b）上的驻点；

②计算f(x)在驻点和端点的函数值，比较而知，最大的一个是最大值，最小的一个是最小值。

（三）函数的图象的作法

中学数学教材中介绍的描点法作函数图象，作图比较粗糙不准确，一般只适用于简单的函数，但对比较复杂的函数就很难作出。现用导数的知识来作函数图象就相当的简便。作函数图象的一般程序：

① 求出函数的定义域；

②考察函数的奇偶性、周期性；

③求函数的一些特殊点，如与两坐标轴的交点等 列表；

④确定函数的单调区间，极值点，凸性区间及拐点 列表；

⑤考察渐进线；

⑥画图

二、几何方面的应用

（一）应用导数的几何意义，求解一般曲线的切线和法线

在解析几何中，我们求曲线的切线和法线，只需要知道曲线的方程和曲线上的任意一点，利用对函数求导就可以得到这一点的切线方程和法线方程.

下面给出求曲线的切线和法线方程的方法步骤：①通过求导数，得到曲线在该点的切线的斜率；②在已知切点坐标和切线斜率的条件下，利用点斜式求出切线方程：

法线方程：上点（2，2） 的切线以及法线方程.

解： 对函数

求导得

所以所以在点（2，2）的切线方程为

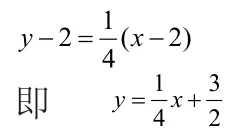
又因为法线方程

即

所以切线方程：，法线方程：

（二）若曲线以参数方程给出，则过曲线上任一点的

切线方程为：

法线方程为：

注：若曲线是由坐标方程给出同样可导出切线方程和法线方程，但记住这些方程倒不如直接计算方便.

三、导数在数列中的应用

在中学数学中，数列与导数、向量、三角与导数的综合题，题目新颖，但难度不大，准确应用导数知识是解该题的关键。此外，数列与函数的关系，用导数解决极为简便。

例2 求证：对于一切工a＞1 成立.

证明 设

于是

因为

故

由于时有，且

故

即内是减函数.

由所以

故

注 在此不等式中，令，可以得到中学数学中常见的一些不等式：

这三题虽然难度系数不大，但是运用导数进行计算就变得更加简便了。

结论

从解决上述五个方面的应用中可以看到，导数在应对复杂的数学问题觉有入手易，过程简便的优势，特别近年来，高考卷对导数的要求逐渐成熟，求导过程并不难，也不是最终落脚点，它的最终目的还是考查函数的性质。解（证明）不等式等重要知识，所以我们不仅要掌握导数的概念，求导的公式和求导的法则及其简单应用，包括求函数的极值、单调区间。证明函数的增减性等，还要学会把导数与其它知识相结合，与寻找求一些复杂问题的简单解法，这样就能占得先机.