基于反思的旋转复习课教学设计与思考

☉江苏南通市通州区平潮实验初中 丛远林

基于反思的旋转复习课教学设计与思考

☉江苏南通市通州区平潮实验初中 丛远林

本节内容是教师复习人教版课标教材九年级上册旋转知识的一节内容，教学设计如下.

一、练习

先请同学们解两道题：

（1）如图1，在△ABC中，BA=BC，D、E是AC边上的两点，且满足∠DBE=∠ABC（0°＜∠CBE＜∠ABC）.以点B为旋转中心，将△BEC按逆时针旋转∠ABC，得到△BE′A（点C与点A重合，点E到点E′处），连接DE′.求证：DE′=DE.

图1

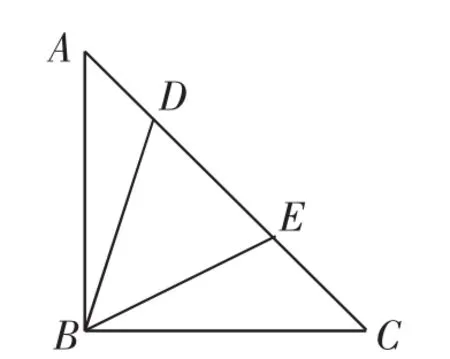
图2

（2）如图2，在△ABC中，BA=BC，∠ABC=90°，D、E是 AC边上的两点，且满足∠DBE=∠ABC（0°＜∠CBE＜ 45°）.求证：DE2=AD2+EC2.

师：第（1）题怎么解？

生1：由旋转和已知条件，易证△BED≌△BE′D，得到DE=DE′.

师：第（2）题呢？

生2：将△BEC绕点B逆时针旋转∠ABC，得到△BE′A，连接DE′（如图3）.由第一题可知DE=DE′，由旋转可知CE=AE′，∠E′AD= 90°，所以DE′2=AD2+AE′2，所以DE2=AD2+EC2.

图3

二、比较法反思1——比较条件和解法的共同处

师：两问中条件有什么共同处？生3：都有BA=BC，∠DBE=∠ABC.

师：两问中解法有什么共同处？

生4：都将△BEC绕点B逆时针旋转∠ABC，得到△BE′A.

【设计意图】掌握比较法反思策略中方法之一，比较条件和解法的共同处.

三、拓展法反思1——研究所有情形

师：第（2）题怎么拓展呢？请小组讨论，再全班交流.

生5：当∠ABC为锐角时（其他条件不变），AD、DE、EC三边中存在两边的平方和等于另一边的平方吗？

生6：不存在.将△BEC绕点B逆时针旋转∠ABC，得到△BE′A，连接DE′（如图4）.由于∠ABC是锐角，所以∠E′AD是钝角，AD、DE′、AE′中不存在两边的平方和等于另一边的平方，所以AD、DE、EC中不存在两边的平方和等于另一边的平方.

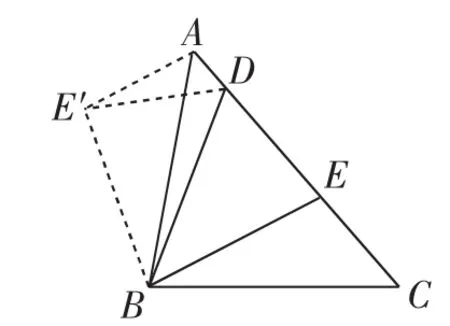
图4

生7：当∠ABC为钝角时（其他条件不变），存在DE2= AD2+EC2吗？

生8：不存在.将△BEC绕点B逆时针旋转∠ABC，得到△BE′A，连接DE′（如图5）.由于∠ABC是钝角，所以∠E′AD是锐角，不存在DE′2=AD2+E′A2，所以不存在DE2= AD2+EC2.

生9：当∠ABC为钝角时（其他条件不变），如存在EC2=AD2+DE2，∠EBC等于多少度？

生10：∠EBC=45°.将△BEC绕点B逆时针旋转∠ABC，得到△BE′A，连接DE′（如图5）.如存在EC2=AD2+DE2，则E′A2=AD2+DE′2，所以∠ADE′=90°，所以∠BDE=45°，所以∠DEB+∠DBE=135°.因为∠DEB=∠C+∠EBC，∠DBE=，所以135°，所以，所以∠EBC=45°.

生11：同样，当∠ABC为钝角时（其他条件不变），如存在AD2= EC2+DE2，则∠ABD=45°.将△ABD绕点B顺时针旋转∠ABC，得到△BCF，连接EF（如图6）.如存在AD2=EC2+DE2，则CF2=EF2+CE2，所以∠CEF=90°，所以∠DEB=45°，所以∠BDE+∠DBE=135°.因为2∠A），所以，所以∠A+，所以∠ABD=45°.

图6

师：拓展法反思，研究所有情形.

【设计意图】掌握拓展法反思策略中方法之一，研究所有情形.

四、拓展法反思2——特殊情形到一般情形

（3）如图7，在正方形ABCD中，E是AB上一点，G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？

师：请同学们先解一下.

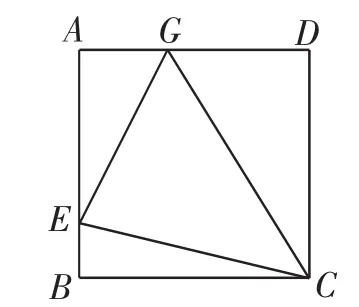
图7

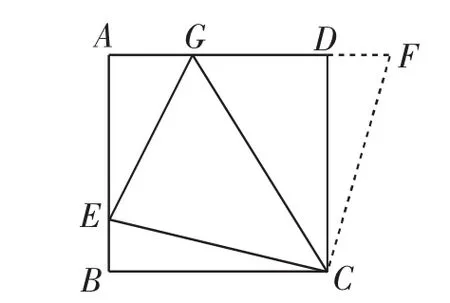
图8

生12：将△EBC绕点C顺时针旋转90°，得到△FDC（如图8），A、D、F共线，易证△CGE≌△CGF，所以EG=GF，所以GE=BE+GD.

师：这一题怎么拓展呢？

生13：对于一般的四边形ABCD，E是AB上一点，G在AD上，如果∠GCE=∠BCD（如图9），四边形ABCD还需满足什么条件，GE=BE+GD仍成立？

师：拓展得好，从特殊情形拓展到一般情形.

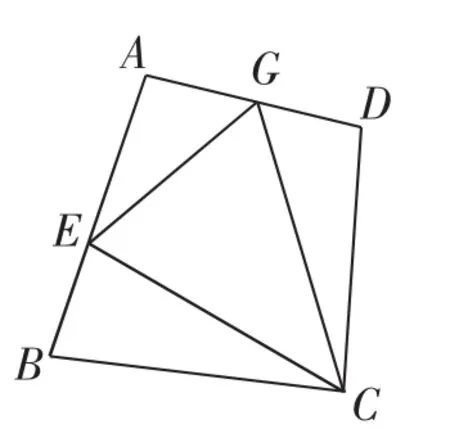
图9

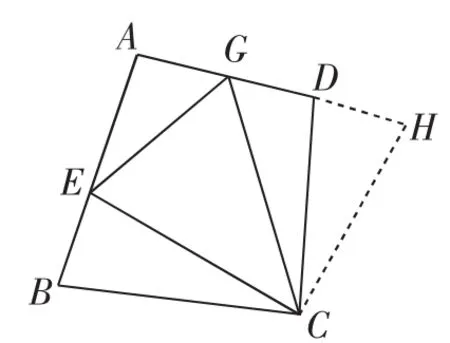
图10

生14：受第（3）题解法的启发，只要将△CBE绕点C顺时针旋转∠BCD（如图10），所得的三角形与△CDG拼成的△CGH与△CGE全等，则GE=BE+GD仍成立，所以必须CB=CD，∠B+∠ADC=180°.

【设计意图】掌握拓展法反思策略中方法之二，从特殊情形到一般情形.

五、比较法反思2——比较图形的本质联系

生15：回到图7，如果截掉△CDG，所得的图形大小和形状不变.在四边形ABCG中（如图11），AG∥BC（BC＞AG），∠B=90°，AB=BC，E是AB上一点，且∠GCE=45°.如果AB、BC的长确定，BE确定，或者AB、BC的长确定，AG确定，那整个图形就确定了，可以求出其余所有线段的长.

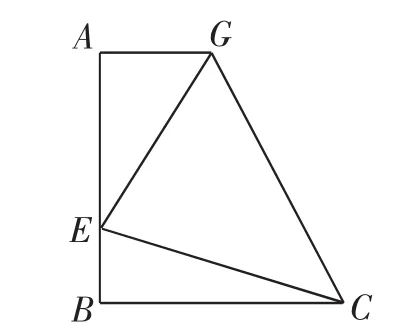
图11

图12

师：太好了，他还是运用比较法反思，比较图形的联系.在图11中，如果已知AB=BC=a，AG=b，那怎么求GE的长？

生16：如图12，补全截掉的△CDG，利用图7的结论GE=BE+GD，设GE=x，则GD=a-b，BE=x-（a-b）=x-a+b，AE=a-（x-a+b）=2a-x-b，在直角三角形AGE中，由勾股定理构建方程就可求出GE.

师：同学们再请看图4、图8、图10，它们看上去差别非常大，本质上有什么共性？能用一个模型来说明吗？

生17：它们本质上都是将一个三角形绕顶点旋转一个等腰三角形的顶角，得到一个三角形.模型如图13所示.

【设计意图】掌握比较法反思策略中方法之二，比较图形的本质联系.

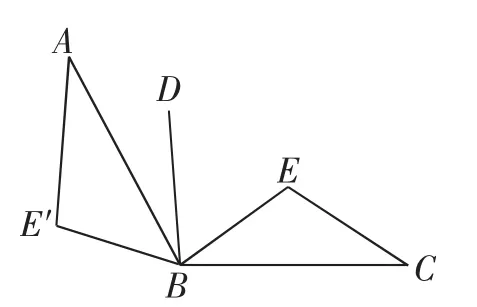
图13

师（总结）：比较法反思：条件、解法、图形上本质的联系.拓展法反思：研究所有情形，特殊情形到一般情形.

教学反思：

目前的复习课，还主要停留在认知层面上，还没有进入元认知领域.元认知包括元认知计划、元认知监控、元认知调节、反思等.它教学生如何制定计划，如何监控自己的思维，思维遇阻时如何调节自己的思维，如何反思.心理学家对思维过程中主要是认知能力与元认知能力共同起作用已达成共识，元认知能力实质上是思维能力的内在组织形式.不培养学生的元认知能力，学生的思维能力发展是不全面的，是不能有本质提升的.国际著名的数学家弗赖登塔尔指出：“反思是数学思维活动的核心和动力.在数学活动中及时、多角度地反思，能促使从新的角度，多层次、多侧面地对问题进行全面考察、分析与思考……对思维能力的提高大有裨益.”因此，本节复习课以反思为载体，深入学生元认知领域，培养学生元认知能力，提升学生思维能力，创新复习课教学.反思不仅仅是对所学知识一般性的回顾或重复，而且是深究学习活动中所涉及的知识、方法、思路、策略等，是对学习活动的总结、提炼、再探索、再发现、再创造.本节复习课就是让学生对旋转学习的再探索、再发现、再提炼，也从中掌握比较法、拓展法的反思策略.

1.陈琦，刘儒德.当代教育心理学［M］.北京：北京师范大学出版社，2004.

2.丛远林.解题后怎样反思［J］.中学数学（下），2013（4）.

3.丛远林.浅谈如何培养学生的元认知技能［J］.中国数学教育（初中版），2012（9）.

4.刘东升，符永平.关注“后半段”：以“有理数复习（1）”研讨课为例——兼谈对复习课的教学思考［J］.中学数学（下），2013（4）.

5.章民.基于数学核心素养的课堂教学实践与反思——以课题“一次函数的概念”课堂教学为例［J］.中学数学（下），2017（3）.

图5