预错的课堂很精彩*——以平方根起始课教学为例

☉广东中山市华侨中学 陈春涛

预错的课堂很精彩*
——以平方根起始课教学为例

☉广东中山市华侨中学 陈春涛

开方运算是初中六大运算中最后学习的一种运算，对比加、减、乘、除、乘方运算，开方尤其是开偶次方（以下只谈开平方）运算非常容易出错.开平方运算为什么容易错？会错在哪儿？教学中应该怎样处理以防止出现这些错误？下面以笔者执教的一堂研讨课为例，谈谈个人的教学建议.

一、学情分析：会错在哪儿

初中的数由两部分构成：符号和绝对值.加、减、乘、除、乘方这五种运算法则都是先确定结果的性质符号，再确定绝对值运算的结果（以下简称为“先确定符号，后确定绝对值”），开方运算也应该如此.所以学生的错误主要集中在符号与绝对值两方面：

一是性质符号容易出错（以下简称为“符号容易出错”）.也就是对于算术平方根和平方根的符号容易混淆.例

如：“9的平方根是3”“已知x2=9，则

二是开方运算结果的绝对值容易出错（以下简称为“绝对值容易出错”）.例如“：

简单地说，就是对平方根的概念和性质在理解上存在障碍，即对运算对象理解不透彻.

二、教材分析：为什么容易错

1.是由教材内容的编排顺序造成的.从章节起始课的特点来看，章节起始课是新知学习的起始，正是学生的学习兴奋点最高的时候，此时学生参与度高，思维也很活跃，正适合承上启下、梳理知识脉络、厘清关键概念.在人教版《义务教育课程标准实验教科书·数学》七年级下册中，编排顺序是先学习算术平方根，再学习平方根.而且为了与生活实际相联系，算术平方根的内容编写比较简单，只有单纯的求平方数的算术平方根.这样的编排容易使学生形成两个认知误区：（1）开平方运算的结果都是正数（符号错误）；（2）带根号的数都能够化简为有理数（绝对值错误）.这种先入为主的印象在学习后续的平方根时就容易形成负迁移.所以，在实际执教过程中，笔者是先学习平方根，再学习算术平方根.

2.是由开方运算本身的算理造成的.每一种运算都是正易逆难.如减法运算比加法运算难，除法运算比乘法运算难.开方是乘方运算的逆运算，比乘方运算更难.从符号方面看，加、减、乘、除、乘方运算结果的性质符号都只有一个，可是开平方运算（非零的数）的符号却有正负两个结果；从绝对值来看，许多有理数开方后的结果都不再是有理数，而是无理数.而且，加、减、乘、除、乘方都概括了明确的运算法则，而开平方并没有专门的运算法则.这些不同造成了开方算理理解的困难.

教材是通过表格、映射图来展现平方与开平方的互逆关系，从而揭示开平方运算算理的.但教材提“求某数的平方根”较多，谈“将某数开平方”较少，学生不能清晰地意识到开平方是一种运算，所以也不能很好地理解开平方运算的算理.

3.是由忽略了对开方运算符号的解读造成的.很多学生能够回答“9的平方根是多少”这样的问题，但却无法回答“9的平方根怎样表示”，所以常常出现“±3”这样的错误.究其根本，是因为学生没有将“视为与“+、-、×、÷”一样的运算符号.所以学生也无法类比加减法运算去理解开平方.例如：“是将9做开平方运算，先确定结果的符号为正，再确定结果的绝对值为3，所以答案为+3”.学生的思考则是“到底是求平方根，还是求算术平方根呢？”

课本例5 求下列各式的值：（1）■ 3 6；（2）- ■0.81；

从上面的两道例题来看，例4是用文字表述求平方根，例5是用符号表述求平方根，但却没有任何一处地方告诉学生“两道例题都是在做开平方运算”“‘’是开平方的运算符号，是求平方根的运算符号”，课本上只是让学生“化简”.

三、教学设计：怎样防止出错

（一）课堂引入.

活动1：理解开方是一种运算.

-3+（ ）=9，-3×（ ）=9，（ ）2=9

引语：第一组的算式分别表示加法运算、乘法运算和乘方运算.第二组则分别是“已知和与一个加数，求另一个加数”，即减法运算；“已知积与一个因数，求另一个因数”，即除法运算.所以，加法与减法互为逆运算，乘法与除法也互为逆运算.那么如果“知道指数与幂，求底数”，又是什么运算呢？它和乘方运算有什么关系呢？

“哪个数的平方等于9”这种运算，我们称为开平方运算，开平方与平方也互为逆运算.对应的，立方与开立方也互为逆运算，即乘方与开方互为逆运算.

加、减、乘、除、乘方运算的结果分别称为和、差、积、商、幂，开平方运算的结果则称为平方根，开立方运算的结果称为立方根.

归纳：如果一个数的平方等于a，那么这个数叫作a的平方根.

求一个数a的平方根的运算，叫作开平方.

口答练习：哪个数的平方等于9？9的平方根是多少？

哪个数的平方等于121（196、256、361、…），这些数的平方根是多少？

展示：（±11）2=121，（±12）2=144，…，（±19）2=361.

设计意图：避免出现性质符号的错误.培养数学运算核心素养的第一步就是理解运算对象，本课需要理解开方运算，理解其运算表达式和结果的含义，故首先从理解平方根是开方运算的结果开始，并且通过结果为整数的开平方运算，让学生形成非零数的平方根有正、负两种情况的直观认识，同时也让学生熟知11～20的平方数.

（二）探求新知.

活动2：认识开平方的运算符号.

例1“因为（±3）2=9，所以9的平方根是±3”.

按上述格式写出下列各数的平方根分别是多少.

设计意图：（1）避免出现性质符号错误.继续深化非零数的平方根有正、负两种情况的直观认识.被开方数从整数逐渐拓展至分数和小数，让学生形成“有理数可以进行开平方运算”的初步认识，为后续判断负数没有平方根作铺垫.

（2）避免出现运算结果（绝对值）的错误.针对第（3）小题，预计学生会出现结果为的错误，出现错误后，让学生自己验算，从而理解计算带分数的平方根时需要转化为假分数来运算.

针对第（4）小题，得到结果为±0.04后，追问学生：哪个数的平方根是±0.4，哪个数的平方根是±0.004？从而让学生学会通过平方检验开平方运算，并且对“被开方数小数点移动两位，平方根的小数点对应移动一位”形成直观认识.

第（5）小题是为引出开平方的运算符号有意设计的.学生开始认识到，并不是每个数的平方根都可以得到有理数结果.如果结果无法写成有理数，则直接表示为的形式.

小结：如果x2=a，那么.如果一个数的平方根无法化简为有理数，则可以直接用含根号的式子表示其平方根.

活动3：掌握平方根的性质.

基础练习：（1）23的平方根表示为________，结果是_______.

（3）±0.16是_______的平方根.

（5）0的平方根表示为_________，结果是________.（6）-9的平方根是多少呢？

归纳：正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根.

设计意图：强化开平方的运算符号.加深对开平方运算的性质符号和运算符号的理解.从正、反两方面理解平方与开平方的互逆关系.

活动4：辨别平方根的性质符号.

例2 说出下列各式的意义，并求出其结果.

判断正误：（1）只有正数才有平方根.

（2）（-1）2的平方根是-1.

（3）-16的平方根是±4.

设计意图：加强对开平方的运算符号与结果的性质符号的理解.学生对于“平方根”三字已经有了直观认知：正数的平方根有正、负两个，可对于“开平方运算”和“平方根的结果”的区别辨别不够清晰，容易出现“±4”这样的错误，所以需要设计一组辨析题，让学生理解“平方根”“平方根中的正值”“平方根中的负值”，从而与其他运算统一起来，即先确定符号，后确定绝对值.并形成带根号的数既有正数又有负数的直观认识.这一环节如果学生理解透彻，则对算术平方根的理解就水到渠成了.

活动5：拓展数的开方运算为式的开方运算.

例3（1）求下列方程中x的值：x2=16.

（2）请观察下列方程，它们是怎样由方程（1）逐步转化的.

x2-16=0；（x-2）2-16=0；2（x-2）2-32=0.

设计意图：避免字母（或式子）开方时出现性质符号的错误.学生前面接触的问题都是这样的：“哪个数的

（三）知识小结.

（1）“±”为开平方运算的性质符号，前面只有“+”（或省略）或“-”都表示只是其中的某一个平方根.

（3）“a”被称为被开方数.因为平方的结果是非负数，所以被开方数a必须是非负数，即“a≥0”.其中正数有两个平方根，它们互为相反数；0只有一个平方根是0；负数没有平方根.

（四）课后分层作业.

A层

1.36的平方根表示为_______，化简结果是______.

3.如果数x有两个平方根a和b，则x一定是_____数，a和b的关系是_______.

4.下列各数：-52、（-4）2、0中，没有平方根的是____.

5.如果一个数的平方根是±4，那么这个数是_____.

6.如果某数的一个平方根是-3，那么这个数的另一个平方根是_______，这个数是________.

B层

1（.-10）2的平方根是_____.

5.已知3a-1与13-5a是x的两个相异平方根，求x的值.

四、教学效果反馈

笔者在执教后的一个月内，曾以自己任教班级（45人）为样本，针对易错项目展开四次统计，第一次只考查题目（1）（3），后三次考查以下三种题型.

（1）25的平方根是__________；

（3）解方程：（x-3）2=49.

统计结果（如表1）：

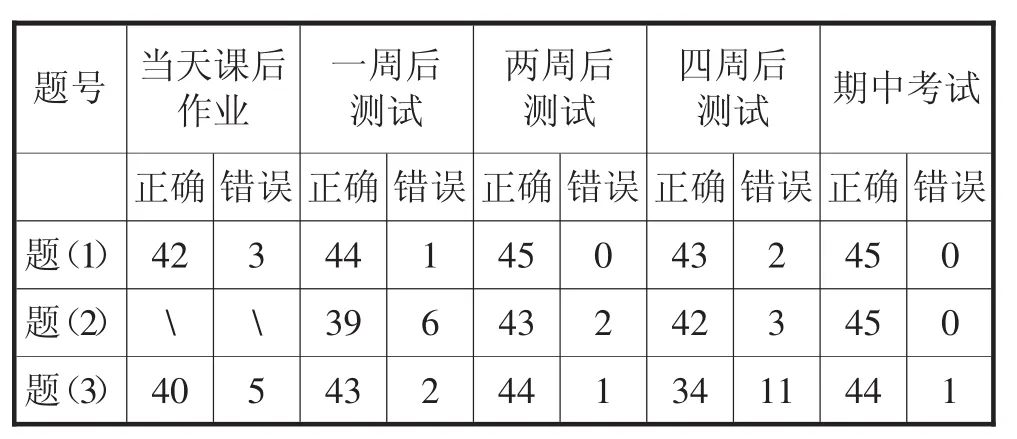
表1

从结果来看，当天的课后作业学生掌握情况不错，绝大部分学生能够正确理解“平方根”的概念，明确算式中带根号的数的符号属性，也能应用平方根的概念解简单的一元二次方程.但这一结果伴随着新知识的学习，数字属性的内容已经明确了，字母属性的式子遗忘与错误开始增多.第四周测试后经过纠正，期中考试前再次复习相同内容时，全班只有1名学生解题（3）时出现错误，其他两题都能全部正确解答.

五、教学反思

1.理解运算对象是培养数学运算核心素养的基础.

数学运算是数学六大核心素养之一.所谓数学运算，是指在明晰运算对象的基础上依据运算法则解决数学问题的思维过程.主要包括：理解运算对象，掌握运算法则，探究运算方向，选择运算方法，设计运算程序，求得运算结果.从数学运算核心素养形成的过程来看，理解运算对象是培养数学运算核心素养的前提与基础.

平方根及其表达形式是学生非常陌生的学习内容，古人经过了近两千年才承认了无理数，才结束了因无理数的产生而带来的第一次数学危机.学生要在一节课内就理解它，无疑是具有相当难度的.故本课的设计需要深入理解概念，逐步渗透学习.整堂课由五个部分构成.（1）认识到开方是一种运算；（2）认识开方的运算符号；（3）理解被开方数的非负要求；（4）认识开平方运算结果的性质符号的意义；（5）将数的开方运算拓展到式的开方运算.这种分解概念认识难点、分步突破重点的设计最终达到了预想的教学效果.

2.课堂教学设计要预设学生可能出现的错误.

军队的训练场上有这样一句话：平时多流汗，战时少流血.课堂训练也是一样，平时将学生容易出现的问题预设更多一些，做到“预设≥生成”，学生在解决问题时就能少走弯路.但是预设错误并不是直接提醒学生不要犯错误，而是将容易犯的错误恰当地整合在课堂的每个流程中，埋下一个个“演习地雷”，当学生不小心踩上去时，让他自己去体会和总结，从而避免在“战场”上踩上真正的地雷.本堂课中就预设了许多学生容易出现的错误.

例如：为了防止学生出现平方根写不完整的现象，在引例中设计了根据上一行乘方运算中（-3）2=9，填写下一行（ ）2=9；

为了防止学生在带分数和小数的开方时出现错误，设计了例1中的“求的平方根”和“求0.0016的平方根”；

为了防止学生产生“带根号的数都能够化简为有理数”的错误认识，设计了“求7的平方根”；

为了从正、反两方面理解平方根，在基础练习中设计了“±0.16是_______的平方根”；

为正确辨别平方根的概念与性质，设计了六道判断正误的题，每一道都直指学生最容易犯错的细节；

为进一步让学生抽象开方运算的本质，设计了解方程x2=16，以及方程的一系列变化形式.

……

预错的课堂，学生的神经是高度集中的，因为他们不知道何时脚下就埋了一颗“地雷”，所以学习效率也是很高的.教师的备课讲求“预设”，预设什么呢？不就是应当预设学生可能出现的困难或错误吗？

3.教学内容的选择要基于理解数学的需要合理整合与补充.

在实际教学中，仍有许多教师将教材视为“圣旨”，不得对其作出丝毫更改.固然，“教材的结构体系、内容顺序是反复考量的，语言是字斟句酌的，例题是反复打磨的，习题是精挑细选的”，但实施课程改革后，各地市纷纷出台自己的教材，人民教育出版社的教材也是几经修订，故教材虽然具有权威性，但并不妨碍老师的个人解读.而且教材针对的对象是其使用区内的所有学生，势必要照顾大多数，教师根据自己班级的实际情况，根据当地教学的实际要求，根据自己课堂的实际需要，大胆重组教材，这样才是“用教材教，而不是教教材”.

本节课的设计从多方面考虑后，最终决定先学“平方根”，后学“算术平方根”，这样更有利于学生突破性质符号理解的障碍.从初中第一课开始，笔者就与学生一起总结了初中的数“先确定符号，后确定数值（绝对值）”的特点，重组教材，先解决开方运算的符号问题，再解决绝对值的问题，符合本班学生的最近发展区.

为了与后续知识联系，本课还埋下了许多伏笔，如对“被开方数小数点移动两位，平方根的小数点对应移动一位”这一结论，设计了“求0.0016的平方根”；为了让学生理解“被开方数既可以是有理数，又可以是无理数”，设计了判断题“表示π的平方根中的负值”；为了让学生理解设计了化简

对平方根的认识是初中数的运算中最困难的内容，笔者尽管作出了一些尝试，但也存在许多瑕疵，如学生对形如“x2=16”的问题频繁出错，故抛砖引玉，以待大家.

1.史宁中.推进基于学科核心素养的教学改革［J］.中小学管理，2016（2）.

2.华志远.数学核心素养的内涵与构成［J］.教育研究与评论（中学教育教学），2016（5）.

3.秦佑春，刘伯新.学“实数”，你会出现这些错误吗？［J］.数理天地（初中版），2008（12）.

4.周玉.教材研究：编排意图指向何方？——以人教版“平方根”教学编排为例［J］.中学数学（下），2015（3）.

*本文系广东省中山市2016年度规划课题“人教版初中数学教材章节起始课的教学策略研究”（立项号：C2016183）的研究成果之一.