主题突出与目标聚焦：习题课的教学追求<br/>——以“角平分线的性质”习题课为例

主题突出与目标聚焦：习题课的教学追求
——以“角平分线的性质”习题课为例

2017-06-26江苏如皋市白蒲初级中学徐小燕

中学数学杂志 2017年12期

☉江苏如皋市白蒲初级中学徐小燕

主题突出与目标聚焦：习题课的教学追求
——以“角平分线的性质”习题课为例

☉江苏如皋市白蒲初级中学徐小燕

八年级学生在初学“全等三角形”一章后，对于角平分线的性质有了新的认识，特别是从“正、反”两个角度探究了“角平分线上的任意一点到角的两边距离相等”这个命题的正确性.在不少涉及角平分线的几何较难题突破时，需要适时添加两条垂线段（为了表述的方便，如图1，我们称这种图形为“双垂直”基本图形），创造条件运用角平分线的性质.

然而根据我们的教学经验，不少学生在涉及添加辅助线时，往往显得还不适应，所以在全等三角形一章复习时，我们预设了一节习题课，主题是复习与角平分线相关的辅助线添加的策略.本文先记录该课选用的典型问题（限于篇幅，不给出这些例题讲评之后的跟进练习），并跟进解读选题、讲评意图，供研讨.

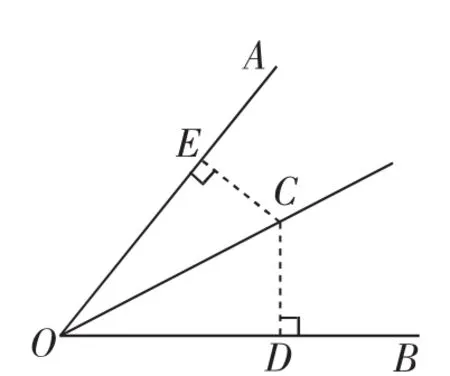
图1

一、教学课例中选用例、习题及讲评预设

例1 如图2，在Rt△ABC中，∠BAC=90°，AB=11，AC=7，射线AM平分∠BAC.射线AM上有一点N到△ABC的顶点B、C的距离相等，连接NB、NC.求四边形ABNC的面积.

图2

图3

预设讲解：由AM平分∠BAC，联想到辅助线，如图3，过N作NH⊥AB，NL⊥AC，垂足分别为H、L.由AN平分∠BAC，可得NH=NL，不难证出△ANH≌△ANL，△BHN≌△CLN.可得AH=AL，BH=CL，设BH=x，则11-x=7+x，解得x=2，所以AH=AL=9，所以S四边形ABNC=S正方形形AHNL=92=81.

回顾反思：如果不能成功求解，究其原因，并不是没有想到辅助线，而是辅助线带来的两组全等三角形信息交叉叠合，没有理出一个等量关系，构造方程的思路受阻.

例2 如图4，已知△ABC中，∠ABC=100°，∠CBD=∠ACB=20°，CE是∠ACB的平分线，D是AC上一点，求∠CED的度数.

图4

预设讲解：作EN⊥AC，EM⊥BD，EP⊥CF，垂足分别是N、M、P.

因为∠1=∠2，所以EN=EP.①

因为∠ABC=100°，∠CBD=20°，所以∠ABM=∠ABP= 80°，从而EM=EP.②

由①和②知EM=EN.又EN⊥AD，EM⊥BD，所以∠3=∠4=（20°+20°） =20°.

所以∠CED=∠4-∠2=20°-10°=10°.

回顾反思：在推证过程中发现“∠ABM=∠ABP”非常关键，引导学生想清图形中再次出现“双垂直”基本图形.

拓展思考：例2中的“三垂直”基本图形其实是不同的“双垂直”出现在同一个几何问题中，我们还可为“三垂直”赋予更多的内涵，比如例3.

例3 如图5，AD是△ABC的角平分线.

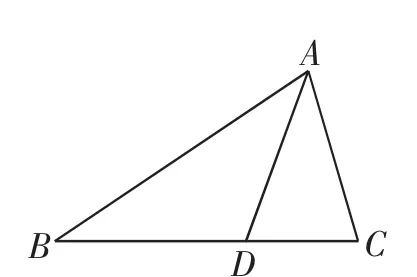
图5

（1）若AB=8cm，AC=5cm，点D到AC的距离是2cm，求△ACD的面积.

（2）在（1）的条件下，能否求出△ABC的面积？如果能，则求之；如果不能，请说明理由.（3）小凡解完（1）和（2）后，经过反思发现请判断“小凡发现”是否正确，并写出你的理解.

预设讲解：（1）如图6，作DE⊥AC于点E.

由点D到AC的距离为2cm，可得DE=2cm.所以S△ACD=AC·DE=5（cm2）.

（2）能求出.理由如下.如图6，作DF⊥AB于点F.

图6

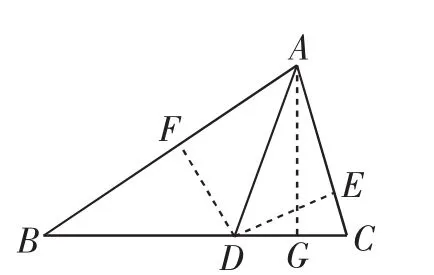
图7

由AD平分∠BAC，DF⊥AB，DE⊥AC，得DF=DE= 2cm.

则S△ABC=13cm2.

（3）小敏的发现是正确的，理由如下.

由S△ABD∶S△ACD=且DE=DF，可得S△ABD∶S△ACD=AB∶AC.

如图7，作AG⊥BC于点G.

虽然产业链金融中潜在的风险整体较少，但是财务公司依然不能忽略风险的预警与控制，但是现阶段财务公司在风险控制方面的能力整体不够理想。由于财务公司自身与商业银行存在差距，所以财务公司的资金规模、金融产品种类以及金融功能等方面都相对不如商业银行，整体表现出抵御风险的能力较弱。其次，财务公司在识别与处理风险方面的效率还有所不足，很多时候在风险爆发后才采取措施进行风险处理，将会对企业集团和上下游企业的运营都造成影响。

回顾反思：这道题第（2）问需要受到第（1）问的启发，想到辅助线DF；而第（3）问要受到前两问对左、右两个三角形面积的比值“S△ABD∶S△ACD”的启发，想到这两个三角形还可以用不同的边与高相乘，从而想到辅助线AG.事实上，这也是三角形角平分线的一个重要性质，在后续相似三角形学完后，还可以借助相似比的知识证明这个性质.

二、关于习题课选题的一些思考

习题课是一首老歌，当前应试教学的现实下，讲评习题课、讲评试题课占据着相当的比例，如何选题是每位教师在备课时都会遇到的难题.以下就围绕上文中的选例经验，具体阐释一些习题课选题的思考.

1.想清教学目标，让训练主题得以聚焦.

就我们在基本教学观摩、随堂课所见，一般的习题课教学往往是教师拿着一些教辅资料由第1题开始讲解，简单题核对答案，出错多的题目给出过程讲评，经验型教师常常会关注学生的错题资源，然后一题接着一题，把教辅资料上的题目讲完就算是订正结束.还有些经验型教师善于将教辅资料上同类试题归类讲解，把结构相同、相近的习题一并讲解，教学效果自然要好一些.然而，我们认为，就习题课教学来说，首先应该充分思考教学目标，即通过这节习题课的教学，训练的主题是什么，围绕这一教学目标，预设哪些典型问题，这些典型问题来源在哪儿.像上文这样，为了帮助学生积累角平分线性质相关辅助线问题，搜集了一些典型问题，重在这些典型问题的主题一致，并且从构造“双垂直”基本图形到“三垂直”图形的深化.

2.搜集学生错题，让训练目标得以落实.

在构思教学目标的同时，充分了解学情是教学基本问题（即认真思考“教谁？”，教学对象的问题）.一个有效的方式是，对照平时作业反馈中的批阅记录，把学生的错题整理出来，特别是将典型错题查找出来，可以通过拍照收集、投影展示，作为一个重要的教学环节，引导所有学生参与纠错与究错.根据教学经验，学生对这类错例都比较感兴趣，参与纠错的热情高涨，如果错例恰好展示的是自己的，他会更加积极纠错，明辨错因，而其他学生也会积极诊评，尝试分析这些学生出错的深层次原因.

3.预设追问拓展，让师生互动对话深入.

在例题选定之后，一方面要贯通思路，特别是从不同角度想清问题的解法，充分预设不同的思考方法，以便在课堂上能全面应对学生可能不同的思维方式；另一方面就是深刻反思问题结构，也就是洞察问题的深层结构.像上文中的角平分线性质的基本图形就是一种问题结构，当学生忽略或缺少解题念头之后，就引导他们往这个基本图形上想，作为必要的念头启示，以获得思路，突破难点.事实上，我们常常引用数学家所谓“数学，根本上是玩概念的”，从外延来看，针对定理的基本图形而开展形的习题变式训练，引导学生善于转化，在一定意义上说，也是倡导“玩概念”“重视概念”“回到概念来解题”的教学追求.选定例题之后，还有一个重要的备课功夫就是：深入思考例题的拓展与变式，以便在教学进程中，将学生的思维引入深处，也是让教学从封闭走向开放的有效措施.

4.注重变式训练，让讲评效果得到反馈.

近年来《中学数学（下）》刊发了大量的习题课例的文章，我们注意到这些课例在教学环节中，都设计了必要的“变式再练”环节，经过笔者确认（曾在网上以这些变式题的关键词进行检索或拍照搜题软件都没有查到原题），这些变式题多是作者独立改编的，具有较大的原创性或深度改编，这种教学备课的自发追求值得学习，特别是在当下搜题、组卷，简单的拿来主义、直接复制粘贴盛行的大环境，值得我们反思的确实太多.我们认为，在习题课的最后5～10分钟，应该安排针对全课教学内容的变式再练，以便检测学生的学习效果，精准反馈，而不是简单的“大家听懂了吗？（齐答：会了）”.